Точки разрыва функций и их классификация

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел , то функция называется непрерывной справа (см. рис):

х₀

Если односторонний предел , то функция называется непрерывной слева (см. рис.):

х₀

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция Дирихле

не является непрерывной в любой точке х₀.

Пример. Функция f(x) = имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к. (см. рис.):

Пример. f(x) = .

Функция не определена в точке х = 0, но имеет в ней конечный предел , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. можно доопределить данную функцию:

.

График этой функции:

Тема 9 Производная и ее приложения

Лекция 9.1 «Производная»

Учебные вопросы:

1. Производная

2. Основные правила дифференцирования

3. Основные теоремы дифференциального исчисления

4. Раскрытие неопределенностей. Правило Лопиталя

Производная

Производной от функции 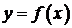называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

Другие обозначения производной: .

Дифференцирование функции – это нахождение производной этой функции. Если функция имеет в точке x производную (конечную), то она называется дифференцируемой в этой точке.

Геометрический смысл производной: производная равна тангенсу угла между осью Ox и касательной, проведенной к графику функции 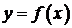в точке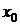 (см. рис.).

Механический смысл: производная пути по времени есть скорость точки в момент 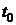т.е. .

Производительность труда в момент 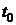есть производная объема произведенной продукции по времени .

Теорема. Если функция 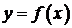дифференцируема в точке 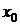, то она в этой точке непрерывна.

Обратная теорема, вообще говоря, не верна, т.е. непрерывная функция может быть не дифференцируемой в точке 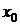, например, функция в точке .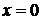

Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс угла наклона секущей МN к графику функции (см. рис.) и

,

где 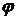- угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой:

Уравнение нормали к кривой: .

Фактически производная функции показывает как бы скорость изменения функции, то как изменяется функция при изменении аргумента.