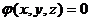Тема 6 Прямая на плоскости. Плоскость и прямая в пространстве
Лекция 6.1. «Прямая на плоскости. Плоскость и прямая в пространстве»
Учебные вопросы:
1. Прямая линия на плоскости
2. Плоскость в пространстве
3. Прямая в пространстве. Взаимное расположение плоскостей и прямых
Прямая линии на плоскости
Геометрия представляет собой математическую модель, воспроизводящую отношения между объектами, которые могут быть в том или ином смысле отождествлены с точками. В аналитической геометрии точка определяется ее координатами в некоторой системе отсчета и, следовательно, геометрические отношения записываются в виде соотношений между координатами (уравнений, неравенств, систем уравнений или неравенств и др.). Далее, если не оговорено особо, применяется декартова прямоугольная система координат.
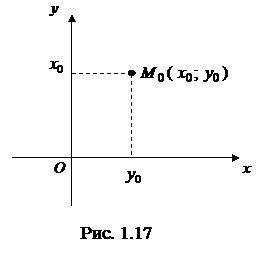
 На плоскости каждая ее точка
На плоскости каждая ее точка 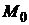 (рис. 1.17) представляется двумя координатами: абсциссой
(рис. 1.17) представляется двумя координатами: абсциссой 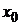 и ординатой
и ординатой 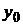 (записывается
(записывается 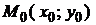 ).
).
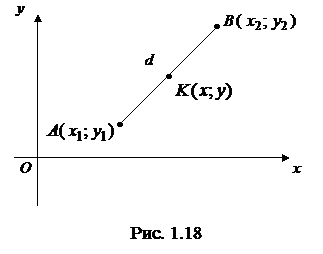
Расстояние 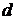 между точками плоскости
между точками плоскости 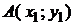 и
и 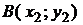
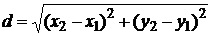 ; (1.3.1)
; (1.3.1)
координаты середины отрезка 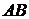 (точки
(точки 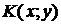 ) (рис.1.18):
) (рис.1.18):
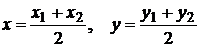 . (1.3.2)
. (1.3.2)
Уравнение вида
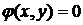 или
или 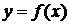 , (1.3.3)
, (1.3.3)
связывающее координаты  и
и  точек плоскости, называется уравнением линии
точек плоскости, называется уравнением линии 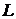 , если:
, если:
a) 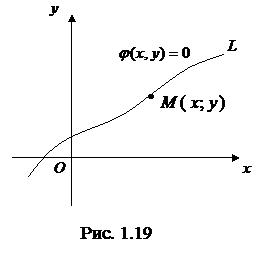 координаты каждой точки
координаты каждой точки 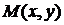 линии
линии 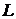 удовлетворяют этому уравнению (рис. 1.19);
удовлетворяют этому уравнению (рис. 1.19);
b) координаты любой точки, не лежащей на линии 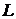 , неудовлетворяют этому уравнению.
, неудовлетворяют этому уравнению.
Уравнение (1.3.3) в общем случае задает на плоскости некоторое точечное множество, которое может быть и не линией на плоскости.
Плоскую линию можно задать также двумя уравнениями
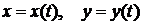 , (1.3.4)
, (1.3.4)
где 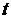 – переменный параметр (параметрическое задание линии).
– переменный параметр (параметрическое задание линии).
Значения координат  и
и  , которые удовлетворяют системе уравнений двух кривых
, которые удовлетворяют системе уравнений двух кривых
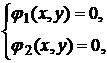
определяют точку пересечения этих кривых. Число точек пересечения равно числу решений этой системы. Если система не имеет решений, то линии не пересекаются.
В зависимости от исходных данных и решаемой задачи уравнение прямой линии на плоскости может иметь различный вид.
Каноническое (симметричное) уравнение прямой. Прямую можно задать точкой 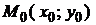 , через которую она проходит, и направлением ее прохождения по направлению вектора
, через которую она проходит, и направлением ее прохождения по направлению вектора 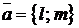 , лежащего на прямой или параллельного ей (рис. 1.20). Этот вектор называется направляющим вектором прямой. Вектор
, лежащего на прямой или параллельного ей (рис. 1.20). Этот вектор называется направляющим вектором прямой. Вектор 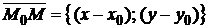 , проведенный из точки
, проведенный из точки 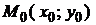 в любую произвольную точку прямой
в любую произвольную точку прямой 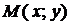 , лежит на прямой и параллелен (коллинеарен) направляющему вектору. Условием коллинеарности векторов является пропорциональность их соответствующих координат, т. е.
, лежит на прямой и параллелен (коллинеарен) направляющему вектору. Условием коллинеарности векторов является пропорциональность их соответствующих координат, т. е.
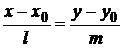 . (1.3.5)
. (1.3.5)
Уравнение (1.3.5) называется каноническим (симметричным) уравнением прямой.
Направление прямой может быть задано вектором 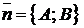 , которому она перпендикулярна (рис. 1.20). Этот вектор называют нормальным вектором прямой. Условием перпендикулярности векторов
, которому она перпендикулярна (рис. 1.20). Этот вектор называют нормальным вектором прямой. Условием перпендикулярности векторов 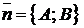 и
и 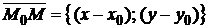 является равенство нулю их скалярного произведения
является равенство нулю их скалярного произведения
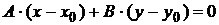 . (1.3.6)
. (1.3.6)
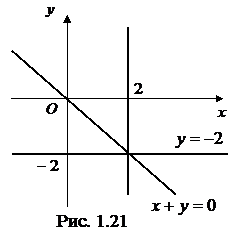 Уравнение (1.3.6) есть уравнение прямой, проходящей через данную точку плоскости перпендикулярно данному вектору.
Уравнение (1.3.6) есть уравнение прямой, проходящей через данную точку плоскости перпендикулярно данному вектору.
Уравнение (1.3.6) можно записать в виде
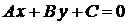 . (1.3.7)
. (1.3.7)
|
 и
и  и определяет при
и определяет при  и
и 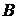 одновременно не равных нулю прямую линию на плоскости. Обратно, каждая прямая линия на плоскости может быть определена линейным уравнением (1.3.7). При
одновременно не равных нулю прямую линию на плоскости. Обратно, каждая прямая линия на плоскости может быть определена линейным уравнением (1.3.7). При 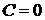 прямая проходит через начало координат. При
прямая проходит через начало координат. При 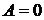 прямая проходит параллельно оси
прямая проходит параллельно оси 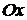 , при
, при 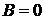 – параллельно оси
– параллельно оси 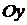 . Для примера на рис. 1.21 приведены прямые, соответствующие уравнениям
. Для примера на рис. 1.21 приведены прямые, соответствующие уравнениям 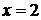 ,
, 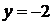 ,
, 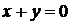 .
. Коэффициенты в общем уравнении прямой (1.3.7) определяют координаты нормального и направляющего векторов этой прямой: 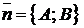 ,
, 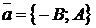 . Следует отметить, что эти векторы определяются с точностью до постоянного множителя, т. е. векторы
. Следует отметить, что эти векторы определяются с точностью до постоянного множителя, т. е. векторы 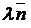 и
и 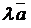 , где
, где 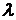 – любое не равное нулю число, также могут быть взяты в качестве нормального и направляющего вектора соответственно.
– любое не равное нулю число, также могут быть взяты в качестве нормального и направляющего вектора соответственно.
Пример. Дана прямая 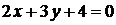 (
( 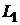 ). Составить уравнения прямых, проходящих через точку
). Составить уравнения прямых, проходящих через точку 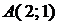 а) параллельно данной прямой (
а) параллельно данной прямой ( 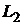 ), б) перпендикулярно данной прямой (
), б) перпендикулярно данной прямой ( 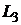 ).
).
◄ а) Направляющий вектор 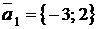 для данной прямой
для данной прямой 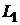 будет направляющим вектором и для
будет направляющим вектором и для 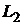 (
( 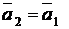 ). Каноническое уравнение прямой
). Каноническое уравнение прямой 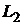 согласно (1.3.5) будет
согласно (1.3.5) будет 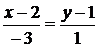 . Отсюда получаем общее уравнение прямой
. Отсюда получаем общее уравнение прямой 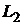 :
: 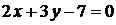 . Это же уравнение можно получить другим путем. Записав общее уравнение прямой
. Это же уравнение можно получить другим путем. Записав общее уравнение прямой 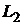 в виде
в виде 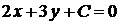 (коэффициенты
(коэффициенты  и
и 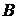 для параллельных прямых можно взять одинаковыми), после подстановки в него координат точки
для параллельных прямых можно взять одинаковыми), после подстановки в него координат точки  получить значение
получить значение 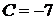 .
.
б) В качестве направляющего вектора прямой 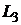 берем нормальный вектор прямой
берем нормальный вектор прямой 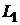 :
: 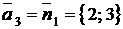 . Каноническое уравнение прямой
. Каноническое уравнение прямой 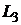 :
: 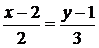 . Отсюда
. Отсюда 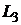 :
: 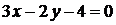 . ►
. ►
Общее уравнение прямой (1.3.7) можно переписать в виде 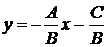 или (положив
или (положив 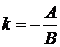 ,
, 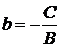 )
)
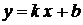 ,
, 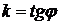 (1.3.8)
(1.3.8)
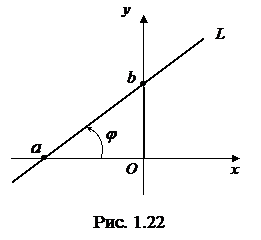 Уравнение (1.3.8) называется уравнением прямой с угловым коэффициентом. Оно определяет прямую, образующую угол
Уравнение (1.3.8) называется уравнением прямой с угловым коэффициентом. Оно определяет прямую, образующую угол 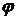 с положительным направлением оси
с положительным направлением оси 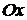 (рис. 1.22) и пересекающую ось
(рис. 1.22) и пересекающую ось 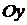 в точке
в точке 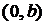 . Коэффициент
. Коэффициент 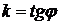 называется угловым коэффициентом прямой.
называется угловым коэффициентом прямой.
Уравнение прямой можно также записать в виде
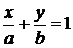 . (1.3.9)
. (1.3.9)
Это уравнение называется уравнением прямой в отрезках и определяет прямую линию, пересекающую ось 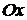 в точке
в точке 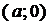 и ось
и ось 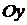 в точке
в точке 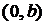 (рис. 1.22).
(рис. 1.22).
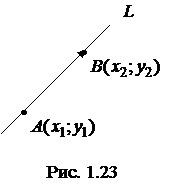 Уравнение прямой, проходящей через две данные(несовпадающие) точки
Уравнение прямой, проходящей через две данные(несовпадающие) точки 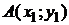 и
и 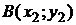 , следует из канонического уравнения (1.3.5), если в качестве направляющего вектора прямой
, следует из канонического уравнения (1.3.5), если в качестве направляющего вектора прямой 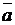 взять вектор
взять вектор 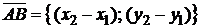 и выбрать точку
и выбрать точку  (или
(или 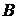 ):
):
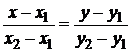 или
или 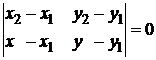 . (1.3.10)
. (1.3.10)
Условием, при котором три точки плоскости 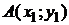 ,
, 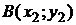 и
и 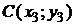 лежат на одной прямой, является
лежат на одной прямой, является
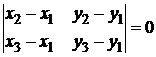 .
.
 Пример. Составить уравнение прямой, проходящей через точки
Пример. Составить уравнение прямой, проходящей через точки 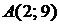 и
и 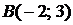 . Записать это уравнение в виде уравнения в отрезках и построить прямую.
. Записать это уравнение в виде уравнения в отрезках и построить прямую.
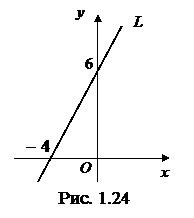
◄ Используя (1.3.10), получаем уравнение искомой прямой: 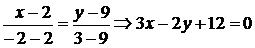 . Переписываем уравнение в форму уравнения в отрезках:
. Переписываем уравнение в форму уравнения в отрезках: 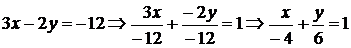 . Из последнего уравнения имеем
. Из последнего уравнения имеем 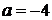 ,
, 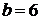 . Прямая приведена на рис. 1.24. ►
. Прямая приведена на рис. 1.24. ►
Обозначив в каноническом уравнении (1.3.5) отношение через 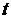 (
( 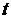 – переменный параметр), получаем параметрические уравнения прямой:
– переменный параметр), получаем параметрические уравнения прямой:
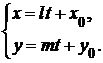 (1.3.11)
(1.3.11)
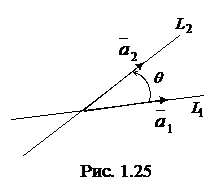 Под углом
Под углом 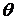 между двумя пересекающимися прямыми
между двумя пересекающимися прямыми 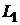 и
и 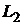 понимается угол, на который нужно повернуть прямую
понимается угол, на который нужно повернуть прямую 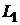 вокруг точки пересечения прямых по часовой стрелке до первого пересечения с прямой
вокруг точки пересечения прямых по часовой стрелке до первого пересечения с прямой 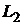 (рис. 1.25). Этот угол (или смежный с ним
(рис. 1.25). Этот угол (или смежный с ним 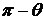 ) равен углу между направляющими векторами
) равен углу между направляющими векторами 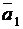 и
и 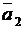 прямых (рис. 1.25), т.е. (с точностью до знака)
прямых (рис. 1.25), т.е. (с точностью до знака)
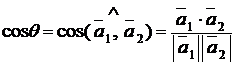 . (1.3.12)
. (1.3.12)
Угол между прямыми можно найти также при помощи их нормальных векторов 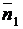 и
и 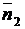 :
:
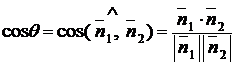 . (1.3.13)
. (1.3.13)
Если прямые заданы уравнениями с угловым коэффициентом 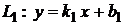 ,
, 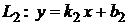 , то угол между ними можно определить по формуле
, то угол между ними можно определить по формуле
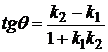 . (1.3.14)
. (1.3.14)
Из этой формулы следует, что прямые параллельны при 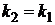 и перпендикулярны при
и перпендикулярны при 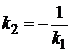 (
( 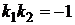 ).
).
Пример. Найти угол между прямыми 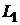 :
: 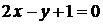 и
и 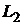 :
: 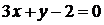 .
.
◄ Используем формулу (1.3.13). По уравнениям прямых находим их нормальные векторы: 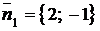 ,
, 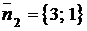 . Согласно (1.3.13) будем иметь
. Согласно (1.3.13) будем иметь 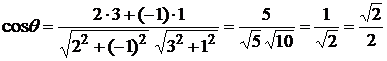 . Отсюда
. Отсюда 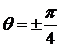 ,
, 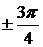 (смежные углы).
(смежные углы).
Используем также формулу (1.3.14). Преобразовав уравнения прямых в форму с угловым коэффициентом: 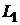 :
: 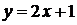 ,
, 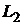 :
: 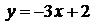 , получаем угловые коэффициенты
, получаем угловые коэффициенты 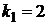 ,
, 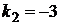 . Подставив значения коэффициентов в (1.3.14), получаем
. Подставив значения коэффициентов в (1.3.14), получаем 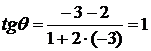 . Отсюда
. Отсюда 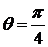 или
или 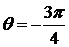 .
.
Получен целый набор значений угла 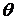 . Значения
. Значения 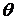 , полученные по формуле (1.3.13), являются на самом деле значениями углов между нормальными векторами прямых и, учитывая неоднозначность выбора этих векторов, неоднозначно определяют угол между прямыми с точки зрения их взаимного расположения на плоскости. Поэтому формулами (1.3.12) и (1.3.13) пользуются тогда, когда взаимное расположение прямых не имеет значения. Однозначное значение угла между прямыми с учетом направления поворота прямой
, полученные по формуле (1.3.13), являются на самом деле значениями углов между нормальными векторами прямых и, учитывая неоднозначность выбора этих векторов, неоднозначно определяют угол между прямыми с точки зрения их взаимного расположения на плоскости. Поэтому формулами (1.3.12) и (1.3.13) пользуются тогда, когда взаимное расположение прямых не имеет значения. Однозначное значение угла между прямыми с учетом направления поворота прямой 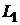 вокруг точки пересечения получают по формуле (1.3.14). Таким образом, угол между данными прямыми
вокруг точки пересечения получают по формуле (1.3.14). Таким образом, угол между данными прямыми 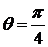 (угол
(угол 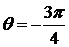 соответствует повороту прямой
соответствует повороту прямой 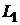 к прямой
к прямой 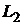 против часовой стрелки). ►
против часовой стрелки). ►
Плоскость в пространстве
 В пространстве каждая его точка
В пространстве каждая его точка 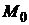 (рис. 1.35) представляется тремя декартовыми координатами: абсциссой
(рис. 1.35) представляется тремя декартовыми координатами: абсциссой 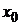 , ординатой
, ординатой 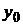 и аппликатой
и аппликатой 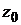 (записывается
(записывается 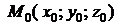 ). Точка также может быть задана своим радиус-вектором
). Точка также может быть задана своим радиус-вектором
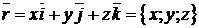 ,
,
проведенным из начала координат в эту точку.
Расстояние 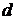 между точками пространства
между точками пространства 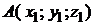 и
и 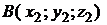
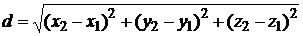 ;
;
координаты середины отрезка 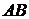 :
:
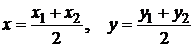 ,
, 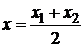
Уравнение вида
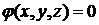 или
или 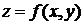 (1.3.26)
(1.3.26)
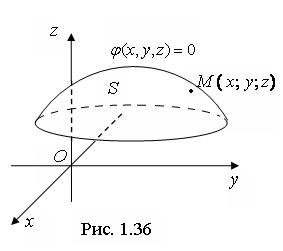 связывающее координаты
связывающее координаты  ,
,  и
и 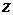 точек пространства, называется уравнением поверхности
точек пространства, называется уравнением поверхности 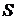 , если:
, если:
a)
|
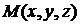 поверхности
поверхности 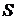 удовлетворяют этому уравнению (рис. 1.36);
удовлетворяют этому уравнению (рис. 1.36); b) координаты любой точки, не лежащей на поверхности 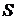 , неудовлетворяют этому уравнению.
, неудовлетворяют этому уравнению.
Уравнение (1.3.26) в общем случае задает в пространстве некоторое точечное множество, которое может быть и не поверхностью в пространстве.
Пример. Уравнение 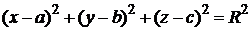 есть уравнение радиуса
есть уравнение радиуса 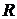 с центром в точке с координатами
с центром в точке с координатами 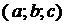 ; уравнение
; уравнение 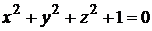 не задает ни одной точки в пространстве (его решением является пустое множество).
не задает ни одной точки в пространстве (его решением является пустое множество).
Значения координат  ,
,  , и
, и 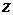 , которые удовлетворяют системе уравнений двух поверхностей
, которые удовлетворяют системе уравнений двух поверхностей
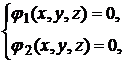
определяют линию пересечения этих поверхностей. Если система не имеет решений, то поверхности не пересекаются.
Уравнение плоскости можно получить следующим образом. Пусть 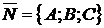 – любой вектор, перпендикулярный данной плоскости
– любой вектор, перпендикулярный данной плоскости 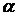 (нормальный вектор плоскости), а
(нормальный вектор плоскости), а 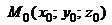 – точка, через которую плоскость проходит (рис. 1.37). Любой вектор
– точка, через которую плоскость проходит (рис. 1.37). Любой вектор 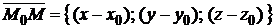 , проведенный из точки
, проведенный из точки 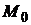 в произвольную точку плоскости
в произвольную точку плоскости 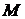 , будет перпендикулярен вектору
, будет перпендикулярен вектору 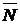 и, следовательно, их скалярное произведение
и, следовательно, их скалярное произведение 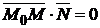 , т. е.
, т. е.
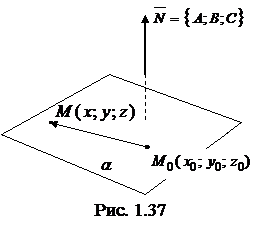
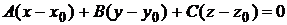 .(1.3.27)
.(1.3.27)
Полученное уравнение есть уравнение плоскости, проходящей через заданную точку 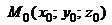 плоскости перпендикулярно заданному вектору
плоскости перпендикулярно заданному вектору 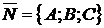 . Оно первой степени относительно декартовых прямоугольных координат (линейно).
. Оно первой степени относительно декартовых прямоугольных координат (линейно).
Уравнение (1.3.27) можно переписать в виде
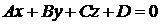 или
или 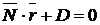 (1.3.28)
(1.3.28)
где 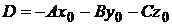 . Это уравнение также линейно относительно координат и называется общим уравнением плоскости: при
. Это уравнение также линейно относительно координат и называется общим уравнением плоскости: при  ,
, 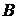 и
и 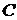 не равных нулю одновременно оно определяет плоскость с нормальным вектором
не равных нулю одновременно оно определяет плоскость с нормальным вектором 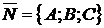 . Обратно, каждую плоскость можно определить уравнением первой степени относительно декартовых прямоугольных координат вида (1.3.28).
. Обратно, каждую плоскость можно определить уравнением первой степени относительно декартовых прямоугольных координат вида (1.3.28).
Пример. Составить уравнение плоскости, проходящей через точку 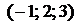 параллельно плоскости
параллельно плоскости 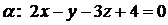 .
.
◄ Так как искомая плоскость 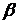 параллельна плоскости
параллельна плоскости 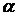 , для нее можно взять в качестве нормального вектора нормальный вектор плоскости
, для нее можно взять в качестве нормального вектора нормальный вектор плоскости 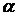 :
: 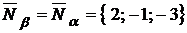
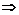
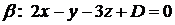 . Величину
. Величину 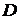 найдем из условия, что искомая плоскость проходит через точку
найдем из условия, что искомая плоскость проходит через точку 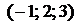 , т. е. координаты этой точки должны удовлетворять уравнению плоскости:
, т. е. координаты этой точки должны удовлетворять уравнению плоскости: 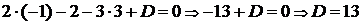 . Окончательно, искомое уравнение плоскости
. Окончательно, искомое уравнение плоскости 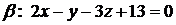 . ►
. ►
Особые случаи положения плоскости относительно системы координат, задаваемых общим уравнением (1.3.28):
1) 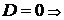 плоскость
плоскость 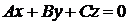 , проходящая через начало координат;
, проходящая через начало координат;
2) 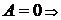 плоскость
плоскость 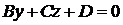 параллельна оси
параллельна оси 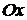 (оси
(оси 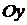 при
при 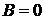 , оси
, оси 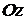 при
при 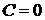 );
);
3) 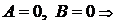 плоскость
плоскость 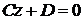 параллельна координатной плоскости
параллельна координатной плоскости 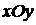 (
( 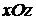 при
при 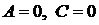 ,
, 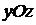 при
при 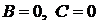 );
);
4) 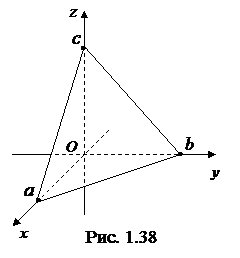
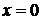 – уравнение координатной плоскости
– уравнение координатной плоскости 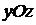 (
( 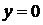 –
– 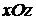 ,
, 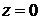 –
– 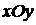 ).
).
Уравнение плоскости в зависимости от решаемой задачи может быть задано в различных формах.
Плоскость, пересекающая ось 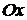 в точке
в точке 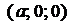 , ось
, ось 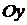 в точке
в точке 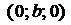 и ось
и ось 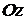 в точке
в точке 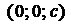 (рис. 1.38) имеет уравнение (уравнение плоскости в отрезках)
(рис. 1.38) имеет уравнение (уравнение плоскости в отрезках)
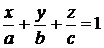 . (1.3.29)
. (1.3.29)
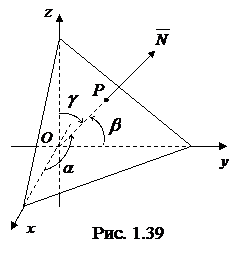 Пусть
Пусть 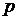 – расстояние плоскости от начала координат (длина перпендикуляра
– расстояние плоскости от начала координат (длина перпендикуляра 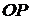 , опущенного из начала координат на плоскость) (рис. 1.39),
, опущенного из начала координат на плоскость) (рис. 1.39), 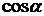 ,
, 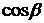 ,
, 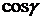 – направляющие косинусы нормального вектора
– направляющие косинусы нормального вектора 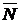 :
: 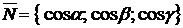 , длина
, длина 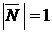 , т. к.
, т. к. 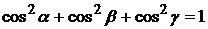 . Тогда уравнение плоскости имеет вид (нормальное уравнение плоскости)
. Тогда уравнение плоскости имеет вид (нормальное уравнение плоскости)
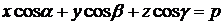 . (1.3.30)
. (1.3.30)
Уравнение плоскости, проходящей через три данные точки 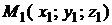 ,
, 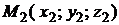 ,
, 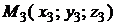 , не лежащие на одной прямой, имеет вид
, не лежащие на одной прямой, имеет вид
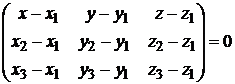 . (1.3.31)
. (1.3.31)
Пример. Составить уравнение плоскости, проходящей через точки 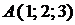 ,
, 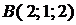 и
и 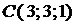 .
.
◄ Подставляя координаты данных точек в формулу (1.3.31), будем иметь 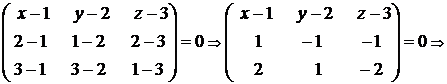
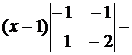
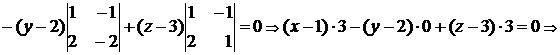
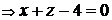 . Так как в полученном уравнении плоскости нет слагаемого с координатой
. Так как в полученном уравнении плоскости нет слагаемого с координатой  , делаем вывод, что она параллельна оси
, делаем вывод, что она параллельна оси 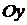 . ►
. ►