Прямая и плоскость в пространстве
Плоскость в пространстве
При рассмотрении плоскости в пространстве необходимо иметь в виду, что методика решения задач аналогична методике решения задач на прямую в плоскости. Это связано с тем, что различные уравнения плоскости в пространстве подобны уравнениям прямой на плоскости.
Приведем уравнения плоскости в пространстве:
- общее уравнение плоскости
- Ах + Ву + Сz + D = 0, (9.1)
где 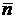 = (А, В, С) – вектор, ортогональный плоскости (вектором нормали);
= (А, В, С) – вектор, ортогональный плоскости (вектором нормали);
-уравнение плоскости в отрезках
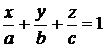 , (9.2)
, (9.2)
где 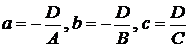 , причем (а, 0, 0), (0, в, 0), (0, 0, с) - координаты точек пересечения плоскости с осями координат;
, причем (а, 0, 0), (0, в, 0), (0, 0, с) - координаты точек пересечения плоскости с осями координат;
- уравнение плоскости, проходящей через точку (х0, у0, z0) с вектором нормали 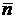 = (А, В, С)
= (А, В, С)
А(х - х0) + В(у - у0) + С(z - z0) = 0, (9.3)
- нормальное уравнение плоскости
хcos a + уcos b + zcos g - p = 0, (9.4)
где р - расстояние от плоскости до начала координат, a, b, g - углы между координатными осями и вектором нормалью к плоскости, направленным от начала координат к плоскости;
- уравнение плоскости, проходящей через три точки (х1, у1, z1), (х2, у2, z2),
(х3, у3, z3)
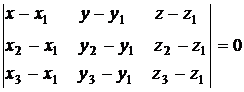 (9.5)
(9.5)
Приведение общего уравнения плоскости (9.1) к нормальному виду (9.4) осуществляется домножением на множитель:
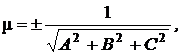
где знак выбирается из условия mD<0.
Расстояние d от точки (х0, у0, z0) до плоскости (9.1) вычисляется по формуле:
d = 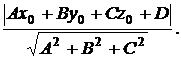 (9.6)
(9.6)
Угол между плоскостями А1х + В1у + С1z + D1 = 0 и
А2х + В2у + С2z + D2 = 0 определяется из формулы:
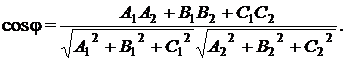 (9.7)
(9.7)
Условие параллельности плоскостей:
А1/А2 = В1/В2 = С1/С2, (9.8)
и условие ортогональности:
А1А2 + В1В2 + С1С2 = 0. (9.9)
Примеры.
а) Приведем уравнение плоскости 2х + 4у - 5z + 21 = 0 к нормальному виду.
Домножив уравнение на нормирующий множитель
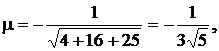
где знак минус взят, так как D>0, получим нормальное уравнение плоскости в виде
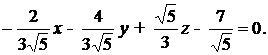
б) Составим уравнение плоскости, проходящей через точку (1, 2, 3) и ортогональную вектору (3, 2, 1).
Из уравнения (9.3) и геометрического смысла коэффициентов уравнения сразу имеем 3(х - 1) + 2(у - 2) + (z - 3) = 0 или
3х + 2у + z - 10 = 0.
в) Найдем уравнение плоскости, проходящей через точку (3, 2, -1) и параллельную плоскости 3х - 5у + 2z - 10 = 0.
В силу параллельности плоскостей векторы нормали у обеих плоскостей можно взять равными, т.е. вектор (3, -5, 2) является вектором нормали нашей плоскости. Тогда из уравнения (9.3) имеем
3(х - 3) - 5(у - 2) + 2(z + 1) = =0 или 3х - 5у + 2z + 3 = 0.
г) Найдем уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z - 3 = 0.
 Для нахождения уравнения заданной плоскости нам необходимо найти вектор нормали
Для нахождения уравнения заданной плоскости нам необходимо найти вектор нормали 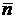 этой плоскости. Так как он ортогонален нашей плоскости, то он ортогонален любому вектору, параллельному этой плоскости. Таким образом, вектор нормали
этой плоскости. Так как он ортогонален нашей плоскости, то он ортогонален любому вектору, параллельному этой плоскости. Таким образом, вектор нормали 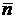 ортогонален векторам
ортогонален векторам 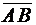 и вектору нормали плоскости х + у + 2z - 3 = 0, т.е.
и вектору нормали плоскости х + у + 2z - 3 = 0, т.е. 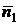 = (1, 1, 2). Из свойств векторного произведения вытекает, что в качестве вектора нормали нашей плоскости можно взять вектор
= (1, 1, 2). Из свойств векторного произведения вытекает, что в качестве вектора нормали нашей плоскости можно взять вектор 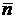 =
= 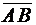 ´
´ 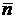 1.
1.
Итак,
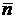 =
= 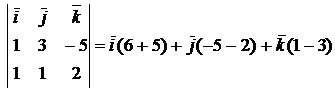 = (11, -7, -2).
= (11, -7, -2).
Из (9.3) теперь легко имеем 11(х - 2) - 7(у + 1) - 2(z - 4) = 0 или
11х - 7у - 2z -21 = 0.
д) Найти угол между плоскостью 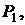 проходящей через точки
проходящей через точки 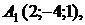
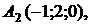
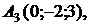 и плоскостью
и плоскостью 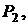 заданной уравнением
заданной уравнением 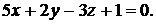
Взяв текущую точку 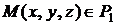 и определив вектора
и определив вектора 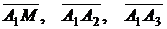 , уравнение плоскости
, уравнение плоскости 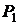 находим по формуле (9.5):
находим по формуле (9.5):
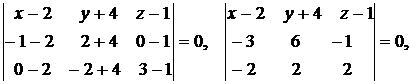
т.е.
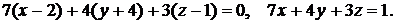
По уравнению плоскостей определяем их нормальные векторы: 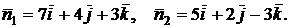 Угол
Угол 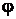 между плоскостями
между плоскостями 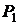 и
и 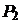 находим по формуле (9.7):
находим по формуле (9.7):
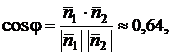
откуда 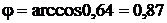 рад.
рад.
9.2. Задачи для самостоятельного решения
а) Написать уравнение плоскости, проходящей через точки А(1, 2, 0) и В(2, 1, 1), перпендикулярно плоскости -х + у - 1 = 0.
б) Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям 2х - у + 3z - 1 = 0,
х + 2у + z = 0.
в) Вычислить объем пирамиды, ограниченной плоскостью 2х-3у+6z=6 и координатными плоскостями.
г) Исследовать взаимное расположение данных пар плоскостей. В случае их параллельности найти расстояние между ними, в случае пересечения - угол между ними:
1) -х + 2у - z + 1 = 0, у + 3z - 1 = 0;
2) 2х - у + z - 1 = 0, -4х + 2у - 2z - 1 = 0.
Прямая и плоскость
Уравнение прямой в пространстве может быть записано как уравнение линии пересечения двух плоскостей в следующем виде:
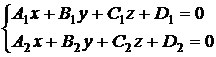 . (9.10)
. (9.10)
На практике больше применяется каноническое уравнение прямой в пространстве
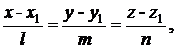 (9.11)
(9.11)
где (х1, у1, z1) - точка, через которую эта прямая проходит, а 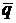 = (l, m, n) - вектор, параллельный прямой, - направляющий вектор.
= (l, m, n) - вектор, параллельный прямой, - направляющий вектор.
Уравнение прямой, проходящей через две точки (х1, у1, z1) и (х2, у2, z2), имеет вид:
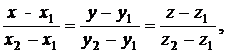 (9.12)
(9.12)
Пример. Составить уравнение прямой, проходящей через точки 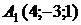 и
и 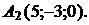
Используя формулу (9.12), получаем
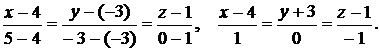
Равенство нулю знаменателя второй дроби означает, что прямая принадлежит плоскости 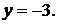
Острый угол между двумя прямыми в канонической форме:
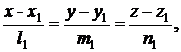
 и
и 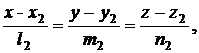
определяется по формуле:
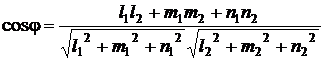 (9.13)
(9.13)
Условия параллельности прямых в канонической форме:
l1/l2 = m1/m2 = n1/n2. (9.14)
Условие ортогональности прямых:
l1l2 + m1m2 + n1n2 = 0. (9.15)
Примеры.
а) Привести уравнение прямой 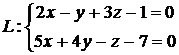 к каноническому виду.
к каноническому виду.
Решение
Выразим из системы х через у и z:
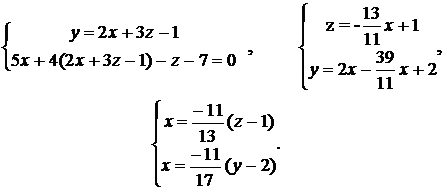
Следовательно,
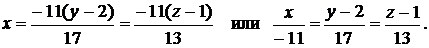
б) Из начала координат опустить перпендикуляр на прямую
(х-2)/2 = (у-1)/3 = (z - 3)/1.
Решение.
Запишем уравнение плоскости, проходящей через начало координат и ортогональной заданной прямой. Так как направляющий вектор заданной прямой 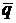 = (2, 3, 1) в этом случае ортогонален плоскости, то можно положить
= (2, 3, 1) в этом случае ортогонален плоскости, то можно положить 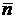 =
= 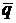 и записать уравнение плоскости в виде 2х + 3у + z = 0. Найдем точку пересечения этой плоскости и прямой для чего решим систему:
и записать уравнение плоскости в виде 2х + 3у + z = 0. Найдем точку пересечения этой плоскости и прямой для чего решим систему:
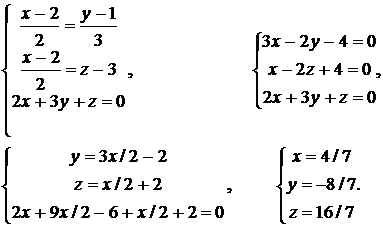
Из уравнения прямой, проходящей через две точки (9.12), получаем искомое уравнение прямой:
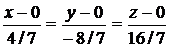 или x = y/(-2) = z/4.
или x = y/(-2) = z/4.
в) Через прямую (х + 1)/2 = (у - 1)/(-1) = (z - 2)/3 проведем плоскость, параллельную прямой х/(-1) = (у + 2)/2 = (z - 3)/(-3).
Решение..
Так как вектора 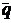 1 = (2, -1, 3) и
1 = (2, -1, 3) и 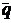 2 = (-1, 2, -3) (направляющие вектора прямых) параллельны плоскости, то их векторное произведение
2 = (-1, 2, -3) (направляющие вектора прямых) параллельны плоскости, то их векторное произведение 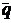 1
1 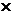
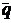 2 ортогонально плоскости, т.е. может быть взято за вектор нормали плоскости.
2 ортогонально плоскости, т.е. может быть взято за вектор нормали плоскости.
Итак,
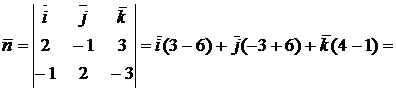 3( -1, 1, 1).
3( -1, 1, 1).
Прямая (х + 1)/2 = (у - 1)/(-1) = (z - 2)/3 лежит в плоскости. Следовательно, и точка (-1, 1, 2), через которую она проходит, находится там же. Таким образом, искомое уравнение плоскости можно записать в виде
-(х + 1) + (у - 1) + (z -2 ) = 0 или х - у - z + 4 =0.
9.4. Задачи для самостоятельного решения
а) Написать уравнение прямой, проходящей через точку А(2, 0, -3) параллельно:
1) вектору 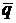 =(2, -3, 5);
=(2, -3, 5);
2) прямой (х - 1)/5 = (у + 2)/2 = (z + 1)/(-1);
3) прямой 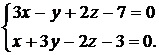
б) Задана плоскость x + y - z + 1 = 0 и прямая (x - 1)/0 = y/2 = (z + 1)/1.
Требуется:
1) вычислить угол между ними;
2) написать уравнение плоскости, проходящей через данную прямую перпендикулярно к данной плоскости.
в) Доказать, что прямые
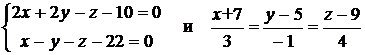
параллельны, и найти расстояние между ними.
г) Найти проекцию точки С(3, -4, -2) на плоскость, проходящую через параллельные прямые

10. ВВЕДЕНИЕ В АНАЛИЗ
10.1. Предел функции. Основные определения и обозначения
Определение конечного предела функции в точке: число А называется пределом функции 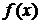 при
при 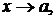 если для любого
если для любого 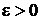 найдется
найдется 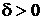 такое, что
такое, что 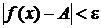 при 0 <
при 0 < 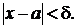
Обозначение: 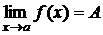 или
или 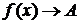 при
при 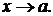
Функция 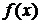
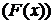 называется бесконечно малой (бесконечно большой) при
называется бесконечно малой (бесконечно большой) при 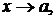 если
если 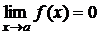
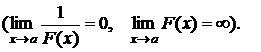
Две бесконечно малые (бесконечно большие) функции 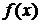 и
и 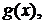 при
при 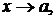 называются эквивалентными, если
называются эквивалентными, если 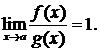
Обозначение: 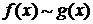 при
при 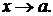
Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной функцией, т.е.
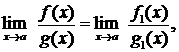 (10.1)
(10.1)
если 
Отметим, что (С- константа)
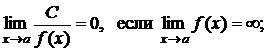

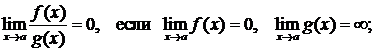
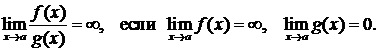
Наиболее простым способом вычисления пределов 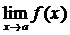 является непосредственная подстановка вместо х числа а. При этом может получится какое-либо число, которое и является пределом. Например
является непосредственная подстановка вместо х числа а. При этом может получится какое-либо число, которое и является пределом. Например
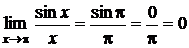 .
.
Второй также несложный случай возникает, если при такой непосредственной подстановке одна из составляющих имеет предел равный ¥ и получаются следующие варианты (и их решение): С/¥ = 0, С/0 = ¥, ¥/0 = ¥,  ,
, 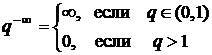 . Например
. Например
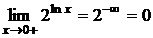 .
.
В остальных случаях возникают так называемые неопределенности. По поведению функций пределы делятся на неопределенности вида: 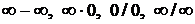 ,
, 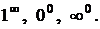 Элементарными приемами раскрытия неопределенностей являются:
Элементарными приемами раскрытия неопределенностей являются:
а) сокращение на множитель, создающий неопределенность;
б) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при 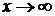 );
);
в) применение эквивалентных бесконечно малых и бесконечно больших;
г) использование двух замечательных пределов:
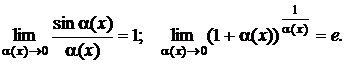 (10.2)
(10.2)
Неопределенности вида 0/0
а) Рациональные выражения. В случае неопределенности 0/0 для рациональных выражений всегда применяется прием сокращения множителя, обращающегося в ноль. Для этого предварительно выделяется линейный множитель, который обращается в ноль. Для выделения линейного множителя находят корни квадратного трехчлена и разлагают его на множители.
Пример. Найти предел
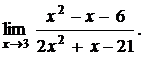
Находим корни числителя х2 - х - 6: х1 = 3, х2 = -2.Разлагаем его на множители х2 - х - 6 = (х – 3)(х + 2). То же самое проделываем и для знаменателя: х1 = 3, х2 = -7/2, 2х2 + х - 21 = 2(х – 3)(х + 7/2) =
= (х – 3)(2х + 7). Подставим эти разложения в предел и сокращаем множители, обращающиеся в ноль:
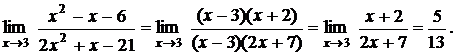
б) Иррациональные выражения. Пределы вычисляются также сокращением множителя, обращающегося в предельной точке в ноль. Правда предварительно для этого иррациональное выражение домножают и делят на сопряженное выражение, т.е., если выражение имеет вид (a ± b), то его домножают и делят на (a 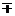 b).
b).
Пример. Найти предел
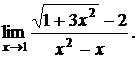
Домножим числитель и знаменатель на выражение 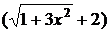 , одновременно разлагая знаменатель на множители:
, одновременно разлагая знаменатель на множители:
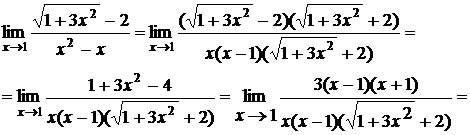
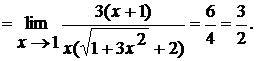
в) Выражения, содержащие тригонометрические и обратные тригонометрические функции. Вычисление пределов в этом случае, как правило, проводится по следующим трем методикам:
1) использование первого замечательного предела
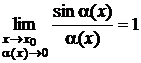
или эквивалентности:
sin a(x) ~ a(x) при a(x) ® 0 (x ® x0 );
2) использование формул тригонометрии;
3) применение замены для сведения к первому замечательному преде-лу.
Примеры.
а) Найти предел
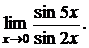
Воспользуемся приведенными эквивалентностями:
sin 5x ~ 5x, sin 2x ~ 2x при x® 0.
Тогда
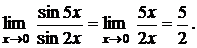
б) Найти предел
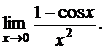
По формулам тригонометрии (1 - cos x = 2 sin2 (x/2)) с учетом эквивалентности имеем
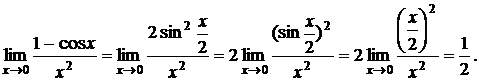
в) Найти предел

Для сведения к первому замечательному пределу сделаем две замены:
у = 1/х, z = arcsin y:
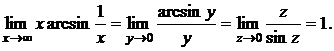
г) Найти предел
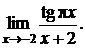
Сделаем замену переменной: у = х + 2. Тогда (с учетом периодичности тангенса и эквивалентности)
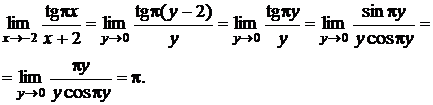
г) Выражения, содержащие логарифмические и показательные функции. Основными приемами вычисления пределов в этом случае являются:
1) использование эквивалентностей
ln(1 + a(x)) ~ a(x), aa(x) - 1 ~ a(x)ln a при a(х) ® 0;
2) замена переменной для сведения к приведенным эквивалентностям.
Примеры.
а) Найти предел
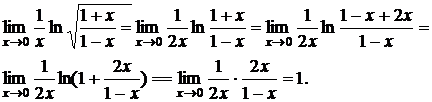
б) Найти предел
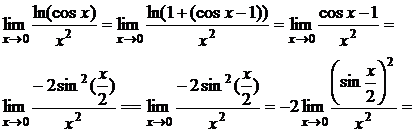
= 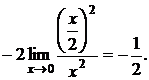
10.3. Неопределенности вида ¥/¥
Основными примерами этой неопределенности являются рациональные функции, когда аргумент стремится к бесконечности. Решаются они вынесением в числителе и знаменателе наивысшей степени х и ее сокращением. При вычислении окончательного результата постоянно используется равенство С/¥ = 0 (C-константа).
Пример. Найти предел
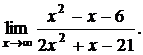
Выносим наивысшую степень х в числителе и знаменателе:
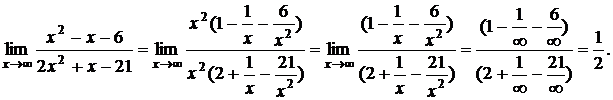
10.4. Неопределенности вида ¥ - ¥, 0×¥, 00, ¥0, 1¥
Первые четыре неопределенности с помощью арифметических преобразований сводятся к рассмотренным ранее случаям. Особый интерес представляет последняя неопределенность. Для вычисления пределов с неопределенностью 1¥ очень удобна следующая формула:
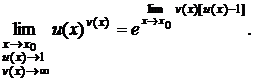
Примеры.
а) Найти предел
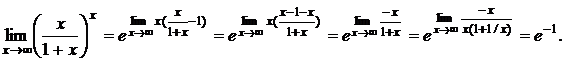
б) Найти предел
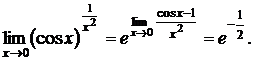
При вычислении подобных примеров наибольшую опасность представляет путаница, возникающая в связи с тем, что к определенным выражениям (типа (2/3)¥ = 0) применяют формулу, как для неопределенности вида 1¥. Например
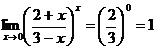 или
или
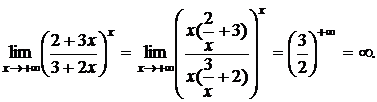
11.1. Производная функции. Основные определения и обозначения
Назовем разность 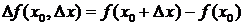 – приращением функции
– приращением функции 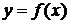 в точке
в точке 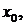 соответствующим приращению аргумента
соответствующим приращению аргумента 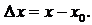 Производной функции
Производной функции 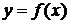 в точке
в точке 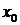 называется предел
называется предел
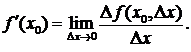
Производная функции 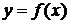 , рассматриваемая на множестве тех точек, где она существует, сама является функцией. Процесс нахождения производной называют также дифференцированием. Для нахождения производных нужно пользоваться таблицей производных основных элементарных функций и правилами дифференцирования функций.
, рассматриваемая на множестве тех точек, где она существует, сама является функцией. Процесс нахождения производной называют также дифференцированием. Для нахождения производных нужно пользоваться таблицей производных основных элементарных функций и правилами дифференцирования функций.
Таблица производных основных элементарных фнкций.
1. 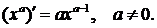
2. 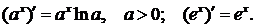
3. 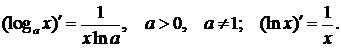
4. 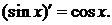
5. 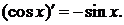
6. 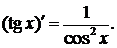
7. 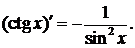
8. 
9. 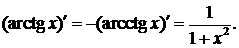
Правила дифференцирования функций
1. Пусть C-константа и функции 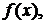
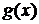 имеют производную в точке
имеют производную в точке 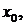 тогда:
тогда:
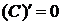 ;
; 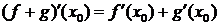 ;
; 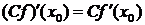 ;
;
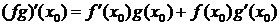 ;
; 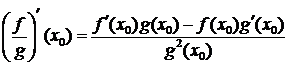 .
.
2. Пусть функция 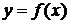 имеет производную в точке
имеет производную в точке 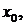 а функция
а функция 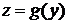 имеет производную в точке
имеет производную в точке 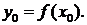 Тогда сложная функция
Тогда сложная функция 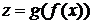 в точке
в точке 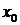 имеет производную, равную
имеет производную, равную 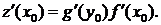
Второе свойство называется правилом дифференцирования сложной функции.
Пример. Найти производную функции 
Полагая 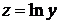 и
и 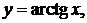 имеем
имеем 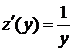 и
и 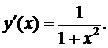 Отсюда, согласно правилу дифференцирования сложной функции, получаем
Отсюда, согласно правилу дифференцирования сложной функции, получаем 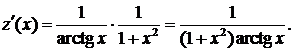
Логарифмической производной функции 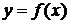 называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е. 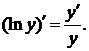 Применение предварительного логарифмирования часто упрощает вычисление производной.
Применение предварительного логарифмирования часто упрощает вычисление производной.
Примеры.
а) Найти производную функции 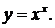
Логарифмируя, получим 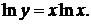 Отсюда находим производные левой и правой части
Отсюда находим производные левой и правой части 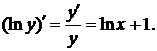 Следовательно,
Следовательно, 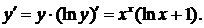
б) Найти производную функции 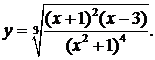
Логарифмируя, получим 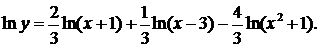 Находя производные левой и правой части, получаем
Находя производные левой и правой части, получаем
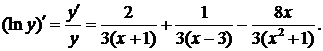
Следовательно, 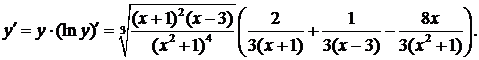
Пусть на интервале 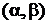 заданы две функции
заданы две функции 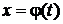 и
и 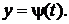 Если при этом функция
Если при этом функция 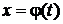 на интервале
на интервале 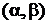 имеет обратную
имеет обратную 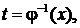 то определена новая функция
то определена новая функция 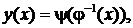 называемая функцией, заданной параметрически соотношениями
называемая функцией, заданной параметрически соотношениями 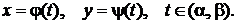 Переменная
Переменная 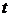 называется в этом случае параметром. Производная функции, заданной параметрически, находится по формуле
называется в этом случае параметром. Производная функции, заданной параметрически, находится по формуле 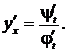
Пример. Найти 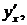 если функция задана параметрически
если функция задана параметрически

Поскольку 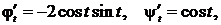 то получаем
то получаем 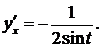
Производной 2-го порядка от функции 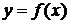 называется производная от ее первой производной, т.е.
называется производная от ее первой производной, т.е. 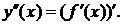 Для производной 2-го порядка используется также обозначение
Для производной 2-го порядка используется также обозначение 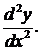
Пример. Найти 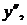 если
если 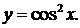
Имеем 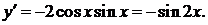 Следовательно,
Следовательно, 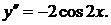
Если приращение функции 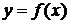 точке
точке 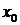 можно представить в виде
можно представить в виде 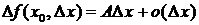 при
при 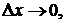 то линейная часть этого приращения
то линейная часть этого приращения 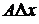 называется дифференциалом этой функции в точке
называется дифференциалом этой функции в точке 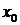 , соответствующим приращению
, соответствующим приращению 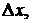 и обозначается символом
и обозначается символом 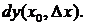
ДОМАШНЕЕ ЗАДАНИЕ
11.1. Основные правила и требования
Каждый студент выполняет один вариант задания. Выбор варианта осуществляется по номеру в журнале группы или по указанию преподавателя. Преподаватель также определяет какие задачи должен решить каждый студент.
Сроки сдачи задания устанавливаются преподавателем.
функции и определить их тип. Построить схематический график функции.
