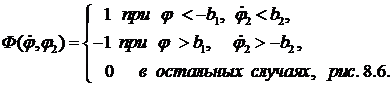Нелинейные автоматические системы

Уравнения нелинейных систем

Упражнение 36.Получить уравнение электромеханической следящей системы, рис.8.1.

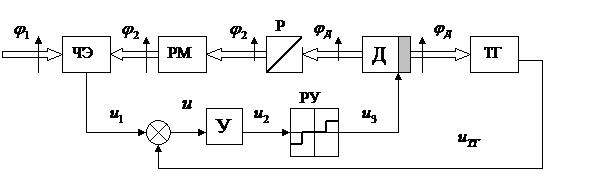
Рис. 8.1. Схема следящей системы

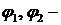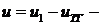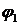На схеме обозначены: углы поворота командной и исполнительной осей; рассогласование (ошибка), чувствительный элемент (датчик угла рассогласования, измеряет углы и 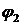, сравнивает их и преобразует результат сравнения в электрический сигнал); У - линейный усилитель; РУ – релейный усилитель; Д – электрический двигатель; Р – редуктор; ТГ – тахогенератор; РМ – рабочий механизм (объект управления).

Уравнения элементов системы и исходные данные:

1. Уравнение чувствительного элемента ;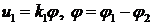

2. Уравнение линейного усилителя ( 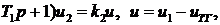где 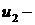напряжение на выходе усилителя, 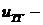напряжение на выходе тахогенератора;

3. Уравнение релейного усилителя, 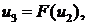где 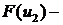нелинейная функция, заданная статической характеристикой, рис.8.2;

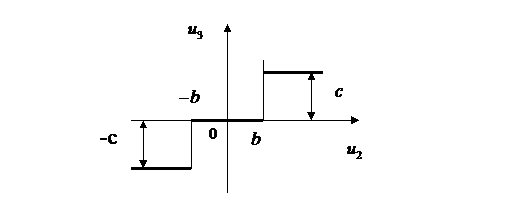
Рис. 8.2. Статическая характеристика релейного усилителя

4.Уравнение исполнительного двигателя 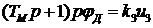, где 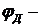угол поворота вала двигателя, 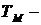электромеханическая постоянная времени, 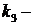коэффициент передачи двигателя;

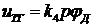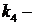5.Уравнение тахогенератора , где коэффициент передачи тахогенератора;

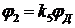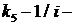6. Уравнение редуктора , где коэффициент передачи редуктора ( 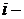передаточное число редуктора).

Рабочий механизм имеет передаточную функцию 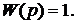Поэтому уравнение РМ отсутствует.

Решение. Составим структурную схему системы. Из содержания схемы следящей системы следует, что она состоит из основного контура с основной обратной связью и дополнительного контура с гибкой обратной связью. С учетом этого структурная схема системы представлена на рис.8.3.

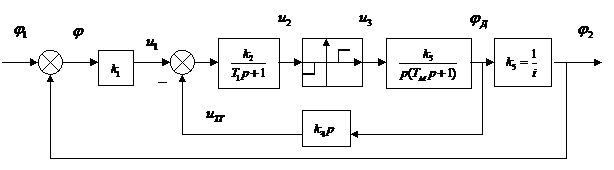
Рис. 8.3. Структурная схема следящей системы

В структурной схеме не представлен рабочий механизм. Это обусловлено тем, что его передаточная функция равна единице и поэтому не оказывает влияния на свойства системы.

Для получения уравнения линейной части системы целесообразно структурную схему на рис.8.3 преобразовать к виду, изображенному на рис.8.4.

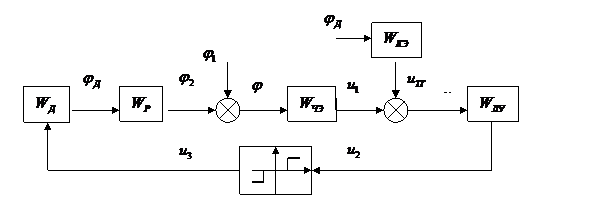
Рис.8.4. Преобразованная структурная схема следящей системы

При составлении структурной схемы применены следующие условные обозначения: 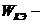передаточная функция корректирующего элемента (тахогенератора); 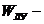передаточная функция линейного усилителя и т.д. Вид передаточных функций элементов системы необходимо получить из их уравнений:

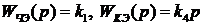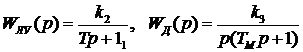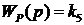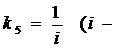, , , передаточное число редуктора).

Из схемы следует: 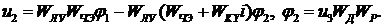Или

.

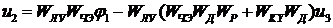После применения выражений для передаточных функций, уравнение системы принимает вид

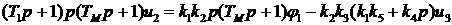
Приведем уравнение системы к стандартному виду

Уравнение линейной части дополняется уравнением нелинейного звена

.

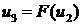Упражнение 37.Составить уравнение системы стабилизации с электромагнитными муфтами и логическим устройством, рис.8.5.

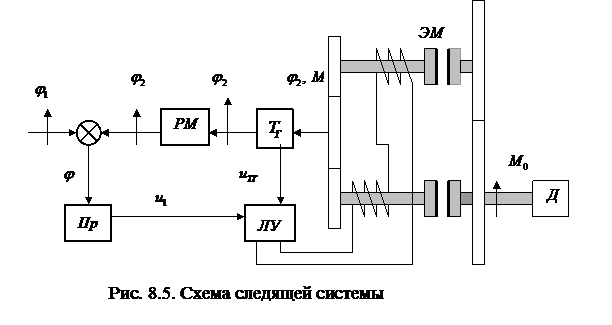
На схеме обозначены: 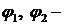углы поворота командной и исполнительных осей; 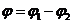- ошибка регулирования; Пр – преобразователь; ЛУ – логическое устройство; ЭМ – электромагнитные муфты с закрепленными на них шестернями; Д – приводной двигатель; РМ – рабочий механизм. ТГ – тахогенератор.

В системе двигатель вращается с постоянной скоростью и в одном направлении. Реверсирование исполнительной оси выполняется переключением электромагнитных муфт по командам логического устройства. Логическое устройство формирует управляющие команды (рис.8.6) в зависимости от поступающих на его вход сигналов 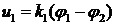и 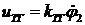. В этих формулах 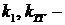коэффициенты передачи чувствительного элемента и тахогенератора.

Требуется получить уравнение системы.

Решение. Запишем закон равновесия моментов, приведенных к исполнительной оси

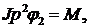(8.1)

где М – вращающий момент, - оператор дифференцирования.

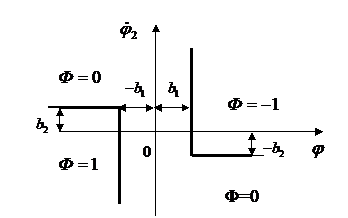
Рис. 8.6. Статическая характеристика логического устройства

Уравнение управляющего устройства, включающего чувствительный элемент, тахогенератор, логическое устройство и электромагнитные муфты трения, можно представить в виде

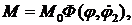(8.2)

где 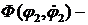нелинейный логический закон, реализуемый в логическом устройстве, статическая характеристика которого изображена на рис.8.6.

Объединяя уравнения (8.1) и (8.2), можем записать уравнение системы в виде

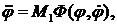(8.3)

где 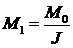;