Корневые методы оценки качества регулирования.

Упражнение 18 . Определить время переходного процесса для системы

,

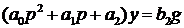где: .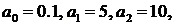

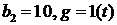Для решения целесообразно использовать корневой показатель качества – степень устойчивости. При этом можно принять, что трубка переходного процесса

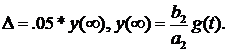
Решение. Для определения времени переходного процесса необходимо найти степень устойчивости. С этой целью в характеристическое уравнение вводится новая переменная 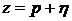. При этом корни характеристического уравнения переместятся на границу устойчивости, т.к. после замены величина корней будет определяться разностью 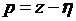. В результате получится смещенное уравнение в виде

,

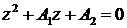где: .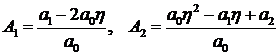

Далее, учитывая, что система находится на границе устойчивости, запишем условие Гурвица, соответствующее этому случаю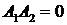

С учетом выражений для 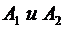и исходных данных данное условие ( уравнение границы) принимает вид

.

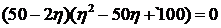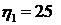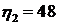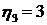Решение уравнения соответствует значениям , и . Для расчета времени переходного процесса применим известную приближенную формулу 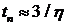.В результате получается три значения для времени переходного процесса: 0,12с, 0,0625с и 1,5с. Очевидно, что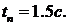

Проверим, так ли это. Запишем уравнение в первой стандартной форме

,

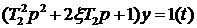где , .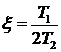

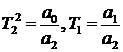С учетом исходных данных: .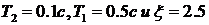

Учитывая, что показатель 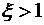, представим систему в виде двух последовательно соединенных апериодических звеньев

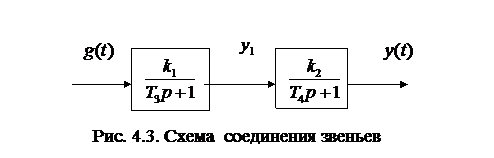
где .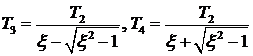

Время переходного процесса для левого звена 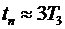, для правого звена 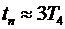. С учетом данных .

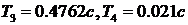Очевидно, что расчетное значение времени переходного процесса 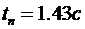. Следовательно, ошибка расчета составляет величину примерно равную 0,07с.

Упражнение 19. Система описывается уравнением

,

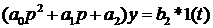где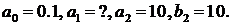

Требуется определить такое значение для коэффициента 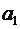, чтобы время переходного процесса 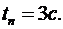. Для решения применить корневой показатель - степень устойчивости, а также принять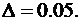

Решение. Введем переменную 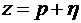и получим смещенное уравнение

,

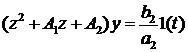где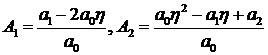

Найдем значение показателя 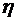, соответствующее времени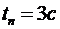

η = 3/t_n.=1.

С учетом значения 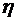=1 и значений коэффициентов 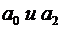находим .

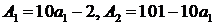Границей устойчивости для смещенного уравнения будет выражение 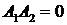или .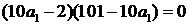

Решение последнего алгебраического уравнения позволяет найти два значения: 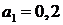и 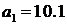. При этом время переходного процесса должно быть равно 3с.

Проверим, так ли это. Пусть 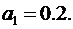Запишем уравнение системы в стандартном виде

,

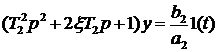где .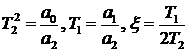

С учетом исходных данных и принятым значением 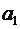=0,2 получим 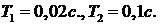и 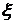= 0,1. Следовательно, имеет место колебательный переходный процесс (рис. 4.4).

На рисунке также показана экспонента, огибающая переходный процесс. Известно описание экспоненты, оно соответствует апериодическому звену

,

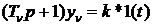где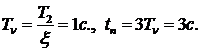

Результат проверки положительный.

Теперь пусть 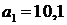. В этом случае 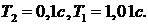и 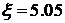. Так как показатель 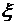>1, то переходный процесс будет соответствовать апериодическому звену второго порядка.

Известно, что данное звено можно представить в виде двух апериодических звеньев первого порядка, соединенных последовательно, рис. 4.3. Там же приведены формулы для вычисления постоянных времени 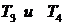. Результаты расчета: 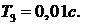и 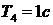. Следовательно,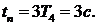

Упражнение 20.Дано характеристическое уравнение

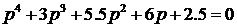
Определить корни уравнения, степень устойчивости 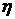, колебательность 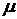, время переходного процесса 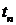и затухание за период .

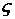Решение. Вычислить корни уравнения целесообразно с помощью функции 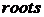, система MATLAB.

Вместо характеристического уравнения запишем выражение для полинома

.

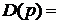
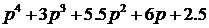Для решения введем в окно 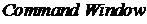следующий набор команд

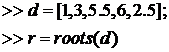
После нажатия клавиши , в этом же окне выводится результат в виде вектор - столбца

r =

-5.0000e - 001 + 1.5000e+000i;

-5.0000e - 001 - 1.5000e+000i;

-1.0000e+ 000 + 5.4159e -009i;

-1.0000e+ 000 - 5.4159e -009i.

Видно, что все корни комплексные. Однако вследствие малости мнимых частей, последние два корня можно считать вещественными. В результате получится следующее: 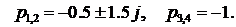Колебательность системы определяется отношением мнимой части комплексного корня к вещественной 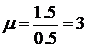. Степень устойчивости 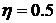. Время переходного процесса 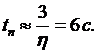Затухание за период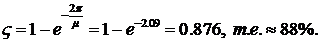

Задача 31. Даны характеристические уравнения:

;

;

;

.

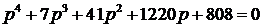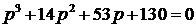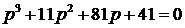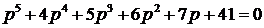Решить предыдущую задачу.

Упражнение 21.Дана передаточная функция разомкнутой системы с астатизмом первого порядка

.

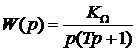Определить соотношение между добротностью по скорости 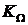и постоянной времени 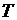, при котором затухание за период будет меньше заданного значения .

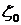Решение. Находим характеристическое уравнение замкнутой системы

.

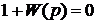С учетом выражения для передаточной функции уравнение принимает вид .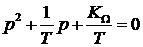

Корни этого уравнения

.

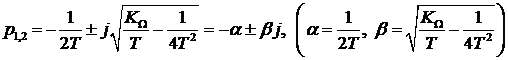Колебательность системы и затухание за один период взаимосвязаны

.

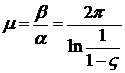Далее находим 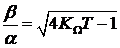. Совместное решение найденного и предыдущего выражений позволяет найти искомую зависимость:

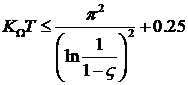
Задача 32. Передаточная функция разомкнутой системы регулирования имеет вид

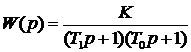
Постоянные времени 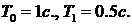. Определить допустимое значение для коэффициента передачи разомкнутой системы 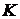, при котором затухание за один период будет не меньше 90%.

Ответ: .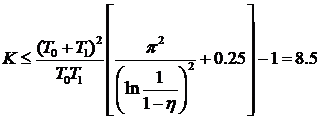

4.3. Частотные методы оценки качества регулирования

Задача 33.На рис. 4.6 изображена амплитудная частотная характеристика замкнутой системы. Определить показатель колебательности.

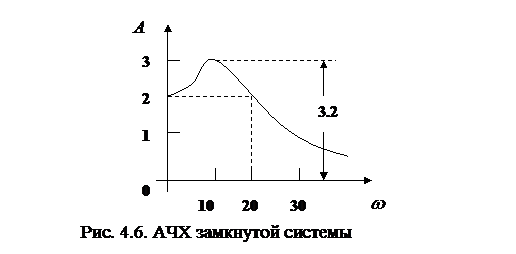
Ответ: .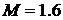

Упражнение 22.Записать аналитически реакцию системы 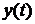с известными характеристиками АЧХ и ФЧХ (рис.4.7) на входное воздействие

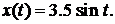
Решение. Общий вид выходного сигнала 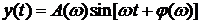. Следовательно, входное воздействие характеризуется параметрами: 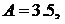смещение по фазе равно нулю, частота .

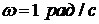Находим для этой частоты по графику 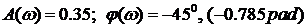. Далее находим амплитуду выходного гармонического сигнала 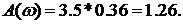Смещение по фазе .

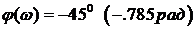Окончательный вид реакции системы имеет вид .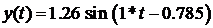

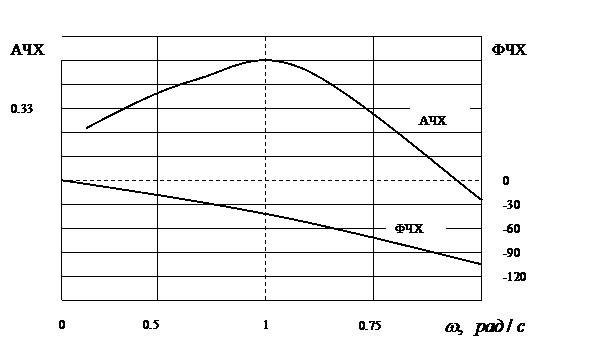
0.31

0.29

0.27

Рис.4.7. Частотные характеристики (лк упр.22)

Задача 34.При входном воздействии 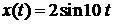найти сигнал 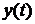на выходе системы с передаточной функцией .

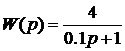Ответ: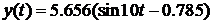

Задача 35.Определить показатель колебательности системы, если передаточная функция разомкнутой системы имеет вид:

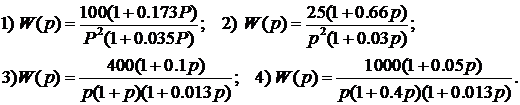
Ответ: М = 1.5, 1.1, 1.3, 1.7.