Другие характеристики центра группирования случайной величины

1.Среднегеометрическое случайной величины Х: G(Х) = e^{M(ln Х)}.

Пусть Х – дискретная случайная величина, имеющая равномерное распределение.

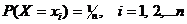, тогда

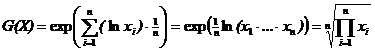– среднее геометрическое.

2. Среднее гармоническое: .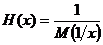

Используется в экономике в индексных расчетах.

3. Медиана: M_e(x) – квантиль x_p, соответствующая вероятности p = 0,5.

Точка х_р, являющаяся решением уравнения F(x_p) = р, называется квантилью распределения. Медиана используется в качестве характеристики среднего, если случайная величина измерена в порядковой шкале.

4.Мода: M₀(x) – это значение случайной величины, соответствующей максимальной вероятности p_i, если X – дискретная величина. Используется для оценки среднего величин, измеренных в номинальной шкале.

Если Х – непрерывная случайная величина, то мода – точка локального максимума плотности распределения.

Если плотность одномодального распределения непрерывной случайной величины симметрична относительно некоторой прямой х = а, то МХ = М_е(х) = М₀(х) = а.

Характеристики вариации случайной величины

Характеристики вариации дают представления о степени отклонения случайной величины от центра группирования. Одной из характеристик вариации является среднее модуля отклонения случайной величины от своего математического ожидания. Для дискретной случайной величины

,

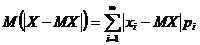для непрерывных

.

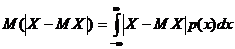Данную характеристику используют редко, так как выражение 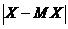задается разными функциями на разных участках. Этого недостатка лишены дисперсия и среднеквадратическое отклонение.

Определение 1.Дисперсией случайной величины X называют число, равное математическому ожиданию квадрата отклонения случайной величины от её математического ожидания:

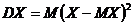. (1)

Если Х – непрерывная, то 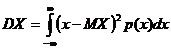. (2)

Если Х – дискретная, то 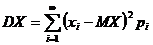. (3)

Формулы (2) и (3) следуют из определения дисперсии и теорем 1 и 2 лекции 13. Часто пользуются другой формулой

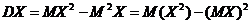. (4)

Доказательство.

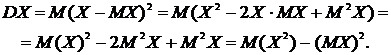
Определение 2. Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсии: .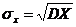

Пример1. Пусть Х – погрешность регистрации веса при взвешивании на весах с ценой деления 1 кг. Y – погрешность с ценой деления 2 кг. Найти DX, DY, σ_x, σ_y.

Будем считать, что погрешности Х и Y равномерно распределены соответственно на интервалах (–0,5; 0,5) и (–1; 1), .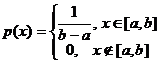

Тогда

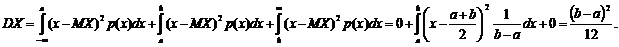Пользуясь выведенной формулой, получим – ; ; ; .

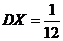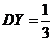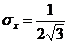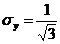По условию задачи один из весов вдвое точнее других, а дисперсии отличаются в четыре раза, в то время как среднеквадратические отклонения отличаются в два раза. Таким образом, среднеквадратическое отклонение может служить мерой точности приборов. Заметим, что единица измерения дисперсии – кг², а единица измерения среднеквадратического отклонения – кг, т.е. среднеквадратическое отклонение измеряется в тех же величинах, что и исходная величина.

Свойства дисперсии

1.Дисперсия постоянной C равна 0,DC = 0, С = const.

Доказательство. DC = M(С – MC)² = М(С – С) = 0.

2. D(CX) = С²DX.

Доказательство. D(CX) = M(CX)² – M²(CX) = C²MX² – C²(MX)² = C²(MX² – M²X) = С²DX.

3. Если X и Y – независимые случайные величины, то

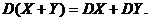
Доказательство.

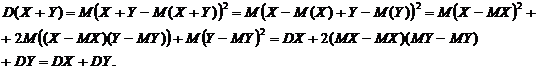
4. Если Х₁, Х₂, … не зависимы, то .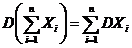

Это свойство можно доказать методом индукции, используя свойство 3.

5. .

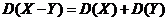Доказательство. D(X – Y) = DX + D(–Y) = DX + (–1)²D(Y) = DX + D(Y).

6.

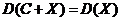
Доказательство. D(C+X) = M(X+C–M(X+C))² = M(X+C–MX–MC)² = M(X+C–MX–C)² = M(X–MX)² = DX.

Пусть 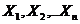– независимые случайные величины, причем , .

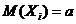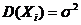Составим новую случайную величину 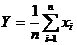, найдем математическое ожидание и дисперсию Y.

; .

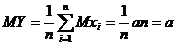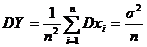
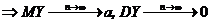То есть при n®¥ математическое ожидание среднего арифметического n независимых одинаково распределенных случайных величин остается неизменным, равным математическому ожиданию а, в то время как дисперсия стремится к нулю.

Это свойство статистической устойчивости среднего арифметического лежит в основе закона больших чисел.