Соглашения для сокращения записи
Договоримся о некоторых соглашениях, сокращающих запись программы для МТ.
1) Если в такте не меняется видимый символ, или автомат не сдвигается, или не меняется состояние автомата, то в соответствующей позиции такта мы не будем ничего писать.
Например, при конфигурации <a, q1> следующие записи тактов эквивалентны:
a,R,q3 ≡ ,R,q3 (но не Λ,R,q3 !!)
b,N,q2 ≡ b, ,q2
a,L,q1 ≡ ,L,
a,N,q1 ≡ , , (это такт останова)
Замечание. Запятые в тактах желательно не опускать, т.к. иначе возможна путаница, если среди символов на ленте могут встретиться буквы L и R.
2) Если надо указать, что после выполнения некоторого такта МТ должна остановиться, то в третьей позиции этого такта будем писать знак «!». Например, такт b,L,! означает следующие действия: запись символа b в видимую клетку ленты, сдвиг влево и останов.
Формально можно считать, что в программе МТ имеется состояние с названием !, во всех ячейках которого записаны такты останова. При этом, однако, такую строку явно не выписывают, а лишь подразумевают.
3) Если заранее известно, что в процессе выполнения программы не может появиться некоторая конфигурация, тогда, чтобы подчеркнуть это явно, будем в соответствующей ячейке таблицы рисовать крестик. (Формально этот крестик считается тактом останова.)
Эти соглашения необязательны, но они сокращают запись программы и упрощают её восприятие.
Входной контроль
1. Расшифруйте аббревиатуру МТ.
2. Что означает символ Λ?
3. Перечислите 3 элементарных действия, которые может выполнять автомат МТ.
Инструктаж по технике безопасности
Ход работы
Задание 1.(перемещение автомата, замена символов)
А={0,1,2,3,4,5,6,7,8,9}. Пусть Р – непустое слово; значит, Р – это последовательность из десятичных цифр, т.е. запись неотрицательного целого числа в десятичной системе. Требуется получить на ленте запись числа, которое на 1 больше числа Р.
Решение:
Для решения этой задачи предлагается выполнить следующие действия:
1. Перегнать автомат под последнюю цифру числа.
2. Если это цифра от 0 до 8, то заменить её цифрой на 1 больше и остановиться; например:
 |  | ||||||||||||||||||
 |  | 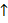 |
3. Если же это цифра 9, тогда заменить её на 0 и сдвинуть автомат к предыдущей цифре, после чего таким же способом увеличить на 1 эту предпоследнюю цифру; например:
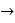 | 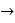 | 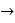 | |||||||||||||||||||
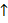 | 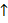 | 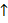 | 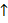 |
4. Особый случай: в Р только девятки (например, 99). Тогда автомат будет сдвигаться влево, заменяя девятки на нули, и в конце концов окажется под пустой клеткой. В эту пустую клетку надо записать 1 и остановиться (ответом будет 100):
 |  |  |  | |||||||||||||||||||||||
 |  |  |  |  |
В виде программы для МТ эти действия описываются следующим образом:
 | ||||||||||||
| q1 | ,R, | ,R, | ,R, | ,R, | ,R, | ,R, | ,R, | ,R, | ,R, | ,R, | ,L,q2 | под последнюю цифру |
| q2 | 1, ,! | 2, ,! | 3, ,! | 4, ,! | 5, ,! | 6, ,! | 7, ,! | 8, ,! | 9, ,! | 0,L, | 1, ,! | видимая цифра +1 |
Задание 2.(анализ символов)
А={a,b,c}. Перенести первый символ непустого слова Р в его конец.
Например:
| a | b | c | b |  | b | c | b | a |
Решение:
Для решения этой задачи предлагается выполнить следующие действия:
1. Запомнить первый символ слова P, а затем стереть этот символ.
2. Перегнать автомат вправо под первую пустую клетку за P и записать в неё запомненный символ.
Как «бегать» вправо, мы уже знаем из предыдущего примера. А вот как запомнить первый символ? Ведь в МТ нет другого запоминающего устройства, кроме ленты, а запоминать символ в какой-то клетке на ленте бессмысленно: как только автомат сдвинется влево или вправо от этой клетки, он тут же забудет данный символ. Что делать?
Выход здесь таков – надо использовать разные состояния автомата. Если первый символ – это a, то надо перейти в состояние q2, в котором автомат бежит вправо и записывает в конце a. Если же первым был символ b, тогда надо перейти в состояние q3, где делается всё то же самое, только в конце записывается символ b. Если же первым был символ c, тогда переходим в состояние q4, в котором автомат дописывает за входным словом символ c. Следовательно, то, каким был первый символ, мы фиксируем переводом автомата в разные состояния. Это типичный приём при программировании на МТ.
С учётом сказанного программа будет такой:
| a | b | c |  | ||
| q1 | 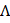 , R, q2 , R, q2 | 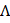 , R, q3 , R, q3 | 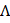 , R, q4 , R, q4 | , R, | анализ 1-го символа, удаление его, разветвление |
| q2 | , R, | , R, | , R, | a, ,! | запись a справа |
| q3 | , R, | , R, | , R, | b, ,! | запись b справа |
| q4 | , R, | , R, | , R, | c, ,! | запись c справа |
Рассмотрим поведение этой программы на входных словах, содержащих не более одного символа. При пустом слове, которое является «плохим» для задачи, программа зациклится – автомат, находясь в состоянии q1 и попадая всё время на пустые клетки, будет бесконечно перемещаться вправо. (Конечно, в этом случае программу можно было бы остановить, но мы специально сделали зацикливание, чтобы продемонстрировать такую возможность.)
Если же во входном слове ровно один символ, тогда автомат сотрёт этот символ, сдвинется на одну клетку вправо и запишет в неё данный символ:
| c | 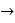 |  | c | ||||||||||
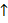 | 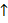 | 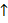 | |||||||||||
| q1 | q4 | ! |
Таким образом, слово из одного символа попросту сдвинется на клетку вправо. Это допустимо. Ведь клетки ленты не нумерованы, поэтому местоположение слова на ленте никак не фиксируется и перемещение слова влево или вправо заметить нельзя. В связи с этим не требуется, чтобы выходное слово обязательно находилось в том же месте, где было входное слово, результат может оказаться и левее, и правее этого места.
Выходной контроль
(выполните самостоятельно по вариантам)
| Вариант 1 | Вариант 2 |
| 1. A={a,b,c}. Заменить на a каждый второй символ в слове P. | 1. A={a,b,c}. Заменить на b каждый второй символ в слове P. |
| 2. A={a,b,c}. Приписать слева к слову P символ b (P → bP). | 2. A={a,b,c}. Приписать справа к слову P символы bc (P → Pbc). |
Контрольные вопросы
На выполнение тестового контроля отводится 12 минут. Работа состоит из 5 заданий.
К каждому заданию с выбором ответа даются 4 варианта ответа, из которых только один правильный. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов. Верный ответ запишите в отчете по практическому занятию.
Тест выбора
Задание №1.
Вопрос: В машине Тьюринга предписание L для лентопротяжного механизма означает…
Варианты ответа:
а) переместить ленту вправо;
б) переместить ленту влево;
в) остановить машину;
г) занести в ячейку символ.
Задание №2.
Вопрос: В машине Тьюринга предписание R для лентопротяжного механизма означает …
Варианты ответа:
а) переместить ленту вправо;
б) переместить ленту влево;
в) остановить машину;
г) занести в ячейку символ.
Задание №3.
Вопрос: В машине Тьюринга предписание S для лентопротяжного механизма означает…
Варианты ответов:
а) переместить ленту вправо;
б) переместить ленту влево;
в) остановить машину;
г) занести в ячейку символ.
Задание №4.
Вопрос: Конфигурация машины Тьюринга, соответствующая начальному стандартному положению
Варианты ответов:
а) 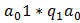 ;
;
б) 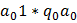 ;
;
в) 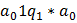 ;
;
г) 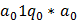 .
.
Задание №5.
Вопрос:Конфигурация машины Тьюринга, соответствующая заключительному стандартному положению
Варианты ответа:
а) 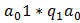 ;
;
б) 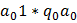 ;
;
в) 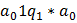 ;
;
г) 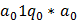 .
.
Условия выполнения:
Задание выполняется письменно в отчете по практическому занятию.
Время на подготовку – 2 мин.
Время на выполнение – 10 мин.
Используются тестовые задания одного типа - тест выбора.
При выполнении заданий в отчете по практическому занятию рядом с номером выполняемого задания записывается номер выбранного ответа.
Критерии оценки:
За каждый правильный ответ выставляется 1 балл.
За не правильный ответ на вопрос выставляется 0 баллов.
Максимальное количество баллов за правильные ответы - 5.
Шкала оценки образовательных достижений:
| Кол-во правильных ответов | Процент результативности (правильных ответов) | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | ||
| 90 ÷ 100 | отлично | ||
| 80 ÷ 89 | хорошо | ||
| 70 ÷ 79 | удовлетворительно | ||
| Менее 3 | менее 70 | неудовлетворительно |
Список литературы
Основные источники:
1. Спирина М.С., Спирин П.А. Дискретная математика – М., 2012. – 368 с.
2. Судоплатов С.В., Овчинникова Е.В. Дискретная математика – М.: Инфра-М, 2011. – 256 с.
Дополнительные источники:
1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике – М., 2008. – 176 с.
2. Канцедал С.А. Дискретная математика – М.: Форум, Инфра-М, 2011. – 224 с.
3. Кочетков П.А. Введение в дискретную математику – М.: МГИУ, 2007. – 88 с.
