Применение логики предикатов к естественному языку
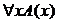 | Для любого x (имеет место)А Для всех x (верно ) A(x) Каждый обладает свойством А Любой объект является А Свойство А присуще всем |
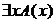 | Для некоторых x (имеет место) А Для подходящего x (верно ) A(x) Существует x, для которого (такой, что) A(x) Кто-нибудь относится (есть) А Хотя бы для одного x (верно) А(х) |
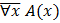 | Не для каждого x (верно) A(x) Не все обладает свойством А А не всегда верно |
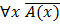 | Для всякого x неверно A(x) A(x) всегда ложно Ничто не обладает свойством А |
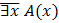 | Не существует x такого, что A(x) A(x) не выполняется ни для какого x Ничто не обладает свойством А Неверно, что для некоторых x A(x) |
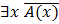 | Для некоторого x не(верно)А(х) Что-то не обладает свойством А |
Входной контроль
1. Как Вы понимаете процесс формализации предложений с помощью логики предикатов?
2. Какие логические операции можно выполнять над предикатами?
3. Какие символы используются для обозначения квантора существования? квантора общности? Каким выражениям в русском языке они соответствуют?
Инструктаж по технике безопасности
Ход работы
1. Пусть х определен на множестве людей М, а Р(х) – предикат «х – смертен». Дать словесную формулировку предикатной формулы 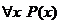 .
.
2. Пусть Р(х) – предикат «х – четное число», определенный на множестве М. Дать словесную формулировку высказыванию 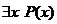 , определить его истинность.
, определить его истинность.
3. Записать предикатной формулой предложения:
а) Любой человек имеет отца;
б) При любом х, не равном нулю, существует у такое, что х/у=2;
в) Для всякого числа х существует такое число у, что х+у=5;
г) Для любого числа у найдется хотя бы одно число х, что y-х<0;
д) Некоторые рациональные числа действительные.
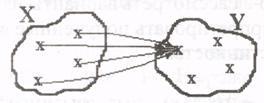
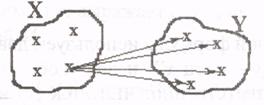
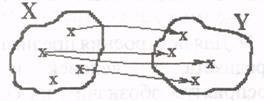
4. Пусть предикат Р(х, у) описывает отношение «х любит у» на множестве людей. Рассмотреть все варианты навешивания кванторов на обе переменные. Дать словесную интерпретацию полученных высказываний.
а) 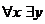 ЛЮБИТ (х,у) б)
ЛЮБИТ (х,у) б) 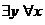 ЛЮБИТ (х,у)
ЛЮБИТ (х,у)
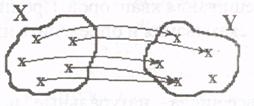
в) 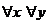 ЛЮБИТ (х,у) г)
ЛЮБИТ (х,у) г) 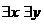 ЛЮБИТ (х,у)
ЛЮБИТ (х,у)
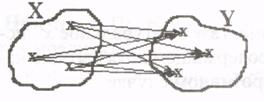
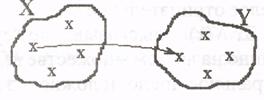
д) 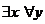 ЛЮБИТ (х,у) е)
ЛЮБИТ (х,у) е) 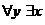 ЛЮБИТ (х,у)
ЛЮБИТ (х,у)
5. Ввести необходимые предикаты и с помощью кванторов записать следующие определения:
а) предела функции в точке;
б) непрерывности функции в точке;
в) параллельных прямых.
Выходной контроль
(выполните самостоятельно по вариантам)
| 1 вариант | 2 вариант |
| 1. Ввести необходимые предикаты и с помощью кванторов записать определение параллельных плоскостей | 1. Ввести необходимые предикаты и с помощью кванторов записать определение непрерывной на интервале функции |
2. Какие из следующих предложений являются предикатами? 1. 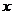 делится на 4 ( делится на 4 ( 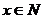 ). 2. ). 2. 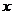 есть отец y ( есть отец y ( 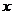 ,y пробегает множество всех людей). 3. ,y пробегает множество всех людей). 3. 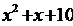 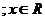 Из предикатов образовать с помощью кванторов высказывания, найти их значения истинности. Из предикатов образовать с помощью кванторов высказывания, найти их значения истинности. | 2. Какие из следующих предложений являются предикатами? 1. 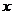 делится на 5. ( делится на 5. ( 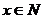 ). 2. ). 2. 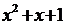 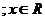 3. 3. 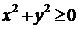 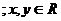 Из предикатов образовать с помощью кванторов высказывания, найти их значения истинности. Из предикатов образовать с помощью кванторов высказывания, найти их значения истинности. |
Контрольные вопросы
На выполнение тестового контроля отводится 12 минут. Работа состоит из 5 заданий.
К каждому заданию с выбором ответа даются 4 варианта ответа, из которых только один правильный. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов. Верный ответ запишите в отчете по практическому занятию.
Тест выбора
Задание №1.
Вопрос: Пусть х, у и z - переменные со значениями из (-∞,∞). Выражение является двуместным предикатом:
Варианты ответа:
а) 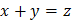 ;
;
б) 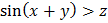 ;
;
в) 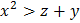 ;
;
г) 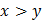 .
.
Задание №2.
Вопрос: Пусть х, у и z - переменные со значениями из (-∞,∞). Выражение не является предикатом:
Варианты ответа:
а) 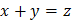 ;
;
б) 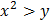 ;
;
в) 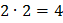 ;
;
г) 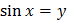 .
.
Задание №3.
Вопрос:Предложение «Для каждого х выполнимо Р(х), но не существует х, что Q(x)» в символическом виде представимо в виде:
Варианты ответов:
а) 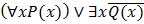
б) 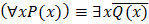
в) 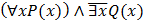
г) 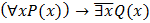
Задание №4.
Вопрос:Пусть даны предикаты на множестве натуральных чисел: Р(х): «х простое число», D(x,y): «х делится на у». Предложение: «Любое простое число не делится на 2, а также не делится на 3» в символьной форме записывается в виде:
Варианты ответа:
а) 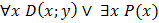 ;
;
б) 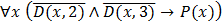 ;
;
в) 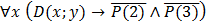 ;
;
г) 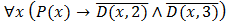 .
.
Задание №5.
Вопрос:Формализация – это:
Варианты ответа:
а) этап перехода от содержательного описания связей между выделенными признаками объекта к описанию, использующему некоторый язык кодирования;
б) замена реального предмета знаком или совокупностью знаков;
в) переход от нечетких задач, возникающих в реальной действительности, к формальным информационным моделям;
г) выделение существенной информации об объекте.
Условия выполнения:
Задание выполняется письменно в отчете по практическому занятию.
Время на подготовку – 2 мин.
Время на выполнение – 12 мин.
Используются тестовые задания одного типа - тест выбора.
При выполнении заданий в отчете по практическому занятию рядом с номером выполняемого задания записывается номер выбранного ответа.
Критерии оценки:
За каждый правильный ответ выставляется 1 балл.
За не правильный ответ на вопрос выставляется 0 баллов.
Максимальное количество баллов за правильные ответы - 5.
Шкала оценки образовательных достижений:
| Кол-во правильных ответов | Процент результативности (правильных ответов) | Оценка уровня подготовки | |
| балл (отметка) | вербальный аналог | ||
| 90 ÷ 100 | отлично | ||
| 80 ÷ 89 | хорошо | ||
| 70 ÷ 79 | удовлетворительно | ||
| Менее 3 | менее 70 | неудовлетворительно |
Список литературы
Основные источники:
1. Спирина М.С., Спирин П.А. Дискретная математика – М., 2012. – 368 с.
2. Судоплатов С.В., Овчинникова Е.В. Дискретная математика – М.: Инфра-М, 2011. – 256 с.
Дополнительные источники:
1. Галушкина Ю.И., Марьямов А.Н. Конспект лекций по дискретной математике – М., 2008. – 176 с.
2. Канцедал С.А. Дискретная математика – М.: Форум, Инфра-М, 2011. – 224 с.
3. Кочетков П.А. Введение в дискретную математику – М.: МГИУ, 2007. – 88 с.
Практическое занятие № 12
Тема: Представление функций в рекурсивной формуле.
Цель: Научиться представлять функции в рекурсивной формуле.
Теоретические основы
Всякий алгоритм однозначно ставит в соответствие исходным данным (в случае если, он определен на них) результат. Поэтому с каждым алгоритмом однозначно связана функция, которую он вычисляет. Исследование проблемы остановки машины Тьюринга показывает, что не для всякой функции существует вычисляющий ее алгоритм. Поэтому в 30-х годах ХХ века была создана теория рекурсивных функций. В этой теории, как и вообще в теории алгоритмов, принят конструктивный, финитный подход, основной чертой которого является то, что все множество исследуемых объектов (в нашем случае функции) строится из конечного числа исходных объектов – базиса – с помощью простых операций, эффективная выполнимость которых достаточно очевидна. Операции над функциями в дальнейшем будем называть операторами.
Пусть имеется некоторый алгоритм α. Областью применимости алгоритма α называют совокупность тех объектов, к которым он применим.
Говорят, что алгоритм α вычисляет функцию f, если его область применимости совпадает с областью определения функции f, и алгоритм α перерабатывает всякий элемент x из своей области применимости в f(x).
Американскими математиками Клини, а впоследствии Черчем были строго определены математические функции, называемые примитивно-рекурсивными. Черч высказал гипотезу о том, что множество всех рекурсивных функций совпадает с множеством всех вычислимых функций. Это предположение получило название тезиса Черча. Гипотеза Черча не может быть доказана, поскольку использует нестрогое понятие вычислимой функции.
Позже американские математики Пост и впоследствии Тьюринг ввели понятие математической машины, которую называют машиной Поста или машиной Тьюринга. Тьюринг высказал гипотезу (известную также как тезис Тьюринга) о том, что для всякой вычислимой функции может быть построена машина Тьюринга. Этот тезис также не может быть доказан, так как включает нестрогое понятие вычислимой функции.
Доказано, что для всякой рекурсивной функции может быть построена машина Тьюринга и, обратно, всякая машина Тьюринга вычисляет рекурсивную функцию.
Известны также другие способы уточнения понятия алгоритма, например, нормальный алгоритм Маркова.
Практический опыт показывает, что тезисы Черча и Тьюринга являются верными, не имеется ни одного опровержения этих утверждений.
Дадим элементарное определение рекурсивных функций.
Рекурсивные функции – это функции, определенные некоторым специальным образом. Из названия следует, что их вычисление содержит обращение к самим себе (при меньших значениях аргументов). Подразумевается, что рекурсивные функции являются арифметическими функциями, т. е. область их определения и область значений является подмножеством множества N0 или совпадает с ним.
Введем следующие правила для получения новых функций из уже имеющихся (1):
1) нуль функция: o(x) = x при каждом 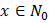 ;
;
2) функция следования: s(x) = x +1 при каждом 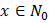 ;
;
3) функция выбора аргумента: 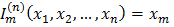 при всех
при всех 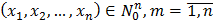 , n =1,2,3...
, n =1,2,3...
Операция суперпозиции (подстановка) заключается в подстановке одних рекурсивных функций вместо аргументов в другие рекурсивные функции.
Функция называется примитивно-рекурсивной, если она может быть получена из исходных функций (1) с помощью конечного числа подстановок и примитивных рекурсий.
Функция называется примитивно-рекурсивной, если она может быть записана с помощью элементарных рекурсивных функций с использованием конечного числа операций суперпозиции и примитивной рекурсии.
Функция называется частичной, если она определена не для всех значений аргументов.
Входной контроль
1. Запишите определения базиса, области применимости алгоритма
2. Сформулируйте тезис Черча.
3. Запишите определения рекурсивной, примитивно-рекурсивной, частичной функций.
4. Какая операция называется суперпозицией?
