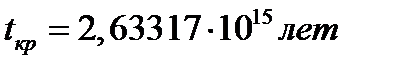Линейная и нелинейная теории накопления повреждений.

Пусть нагрузка представлена в таком виде

F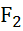

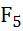
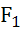
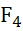
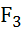
T

Рассмотрим задачу, когда σ= .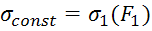

Найдем для него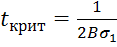

Аналогично найдем 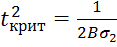. И т.д.

Введем понятие поврежденность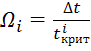

Таким образом, .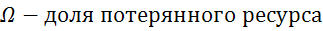

Далее суммируем все потери ресурса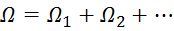

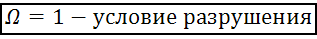
Такой подход называется линейной теорией накопления повреждений.

Примечание: если вычислить 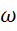по всем правилам, то в любое время истинная потеря меньше упрощенной .

Нелинейная теория

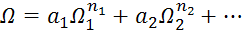
Формула Гриффитса позволяет вычислить предел прочности тела с трещинами.

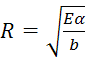, где

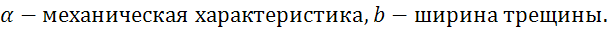
Формула Гриффитса

σ

Вырежем элемент с трещиной

b

σ=0

Δb

t

Задача: найти 𝜎^*

Нарисуем силовые линии

При 𝜎^* полоски начнут разрываться. Трещина возрастет на Δb.

Закон сохранения энергии: энергия растяжения полоски Э в момент разрушения тратится на разрыв межмолекулярных связей. Обозначим эту работу W^*.

Обозначим W^* - энергия на разрушение 1 мм².

Чтобы разорвать полоску, совершается работа:

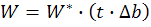
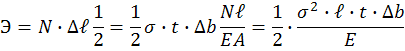
Очевидно, что ℓ чем больше, тем больше b

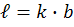
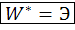
В момент разрушения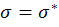

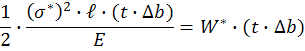
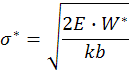
Обозначим =>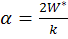

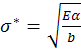
Закон Пэриса

Рассмотрим циклическую нагрузку

σср

σа

σmax

Из-за действия циклической нагрузки трещина начинает расти

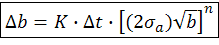
Определение: 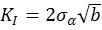– первый коэффициент интенсивности напряжений.

Этот параметр показывает уровень напряженности тела с трещиной при простом растяжении.

Условие разрушения имеет вид: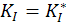

Используем закон Пэриса для оценки ресурса изделия при циклических нагрузках:

– скорость развития трещин

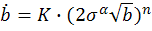
Если 𝜎_𝛼 постоянна ,то решение этого уравнения легко находится

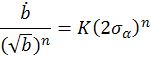
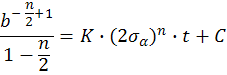
Начальное условие: при b = b_нач =>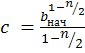

n, K – эксперементальные данные для материала.

Таким образом, можем найти b

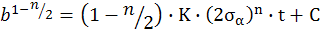
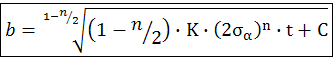
Для материала σ^* - дано из эксперимента

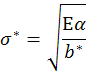
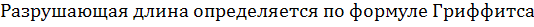
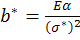
Тогда можно узнать время разрушения из условия b=b^* при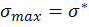

Получим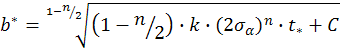

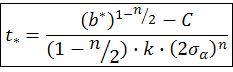
Примечание: если известен закон изменения 𝜎_𝛼 = 𝜎_𝛼(t), то уравнение Пэриса также легко интегрируется (аналитически или численно). В случае, когда в явном виде эта зависимость не известна, то как обычно используют пошаговое численное интегрирование. На каждом шаге определяют

,

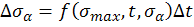а затем вычисляем

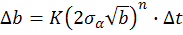
Гибкие конструкции

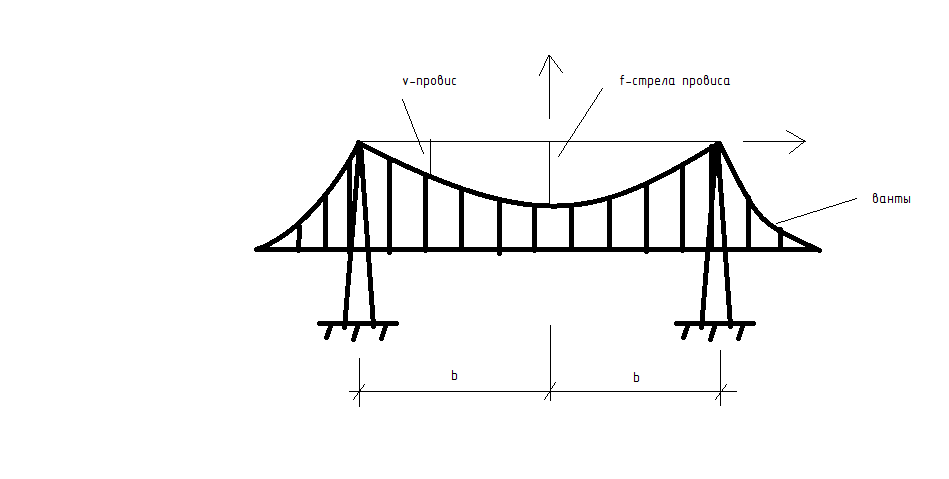
Найти N, v.

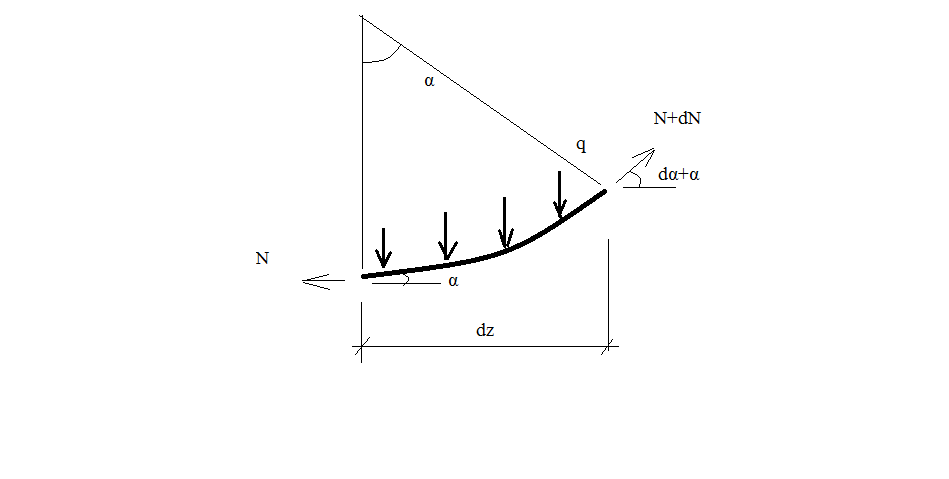
Запишем уравнение равновесия:

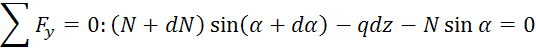
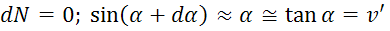
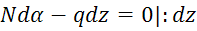
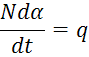
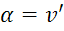
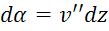
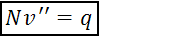(1)

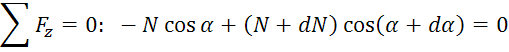
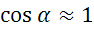
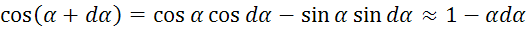
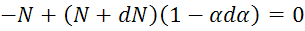
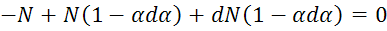
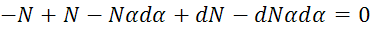
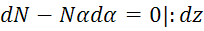
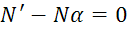
Получили 2 нелинейных уравнения.

Решения такой системы не существует, поэтому она решается приближенно.

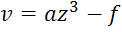
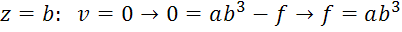
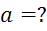
Решение:

(1):

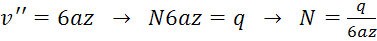
(2):

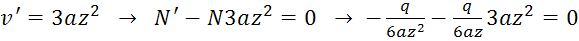
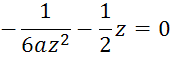
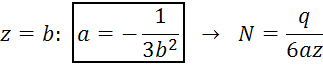
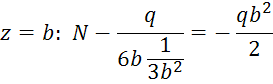
Приближенное решение с использованием условия пологости

Более простое решение получим, если в (2) учтем, что угол наклона мал. Тогда из условия (2) следует, что усилие растяжения будет постоянным:

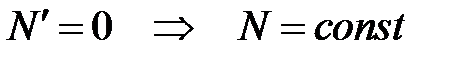
Aппроксимируем 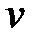в виде, при котором удовлетворяются условия закрепления:

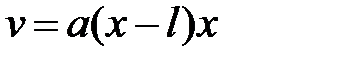(3)

Здесь a - искомая константа.

Тогда из уравнения (1) вытекает, что

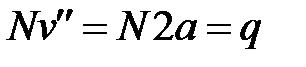(4)

Для того, чтобы найти зависимость N от нагрузки,используем закон Гука. Удлинение ванта подсчитаем приближенно, заменив дугу двузвенной ломаной:

v0

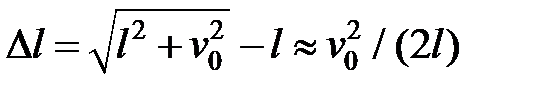
Из закона Гука находим

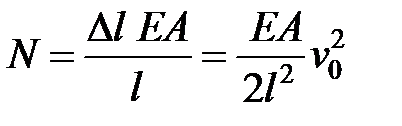(5)

Выразим 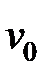через параметр а аппроксимирующей функции.

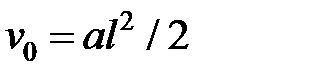(6)

Тогда получим

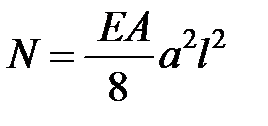
Из уравнения равновесия (4) вытекает окончательное выражение, которое связывает искомый параметр а и нагрузку

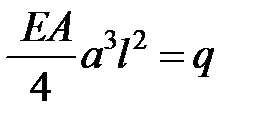
Учитывая по соотношение (6) можно записать зависимость 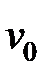и q:

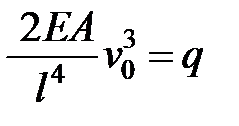
P

b

h

2см

l

l=l0/2

P

l=l0∙1,5

P

l=2l0

P

l=l0

F

P

q2

q1

σ

εb1

εb2

εb0

Rb1

Rb2

Rb0

Найти допустимую нагрузку 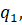(или или 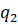, или Р согласно своего варианта) из условия жесткости по прогибам < [

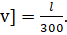
Исходные данные:

Класс тяжелого бетона – брать из таблицы.

Класс арматуры – А500.

Сила 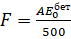приложена центрально.

Остальные данные взять из СП 63.13330.2012.

Использовать диаграмму деформирования бетона, арматуру считать упругой, учесть изменение геометрии колонны.

Номер схемы	l0 (м)	μ %	b (м)	h (м)	q1	q2	P	l1/l	Класс бетона
А	Б	В	Г	Г	А	А	А	B	Б
	4.8	1.1	0,41	0,21			Р	0,61	В 3,5
	4.9	1.2	0,42	0,22	q			0,62	В 5
	5.0	1.3	0,43	0,23		q		0,63	В 7,5
	5.1	1.4	0,44	0,24			P	0,64	В 10
	5.2	1.5	0,45	0,25		q		0,65	В 12,5
	5.3	1.6	0,46	0,26	q			0,66	В 3,5
	5.4	1.7	0,47	0,27		q		0,67	В 5
	5.5	1.8	0,48	0,28			P	0,68	В 7,5
	5.6	1.9	0,49	0,29		q		0,69	В 10
	5.7	1.0	0,50	0,30			Р	0,70	В 12,5

P

b

h

2см

l

l=l0/2

P

l=l0∙1,5

P

l=2l0

P

l=l0

F

P

q2

q1

σ

εb1

εb2

εb0

Rb1

Rb2

Rb0

Найти допустимую нагрузку 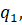(или или 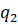, или Р согласно своего варианта) из условия жесткости по прогибам < [

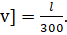
Исходные данные:

Класс тяжелого бетона – брать из таблицы.

Класс арматуры – А500.

Сила 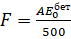приложена центрально.

Остальные данные взять из СП 63.13330.2012.

Использовать диаграмму деформирования бетона, арматуру считать упругой, учесть изменение геометрии колонны.

Номер схемы	l0 (м)	μ %	b (м)	h (м)	q1	q2	P	l1/l	Класс бетона
А	Б	В	Г	Г	А	А	А	B	Б
	4.8	1.1	0,41	0,21			Р	0,61	В 3,5
	4.9	1.2	0,42	0,22	q			0,62	В 5
	5.0	1.3	0,43	0,23		q		0,63	В 7,5
	5.1	1.4	0,44	0,24			P	0,64	В 10
	5.2	1.5	0,45	0,25		q		0,65	В 12,5
	5.3	1.6	0,46	0,26	q			0,66	В 3,5
	5.4	1.7	0,47	0,27		q		0,67	В 5
	5.5	1.8	0,48	0,28			P	0,68	В 7,5
	5.6	1.9	0,49	0,29		q		0,69	В 10
	5.7	1.0	0,50	0,30			Р	0,70	В 12,5

Задача №1

Р

Р

Дано: А_б=120см², А_а=10см², Р=13т, Е_б=100 т/см²,

А Е_а=1000 т/см², η_б=100 тгод/см², с=300, Δt=0,5 год

Закон ползучести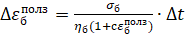

2А Найти: 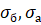в третьей нижней части через 1 год

А

Решение: Уравнение равновесия нижней части:

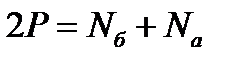
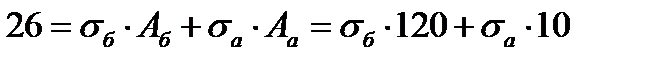
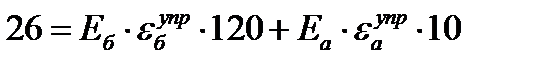
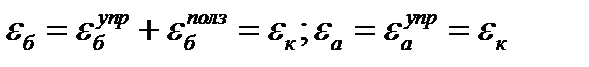
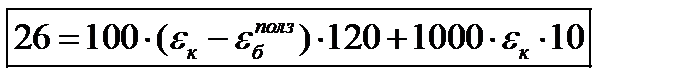
1 шаг: t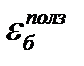=0: =0

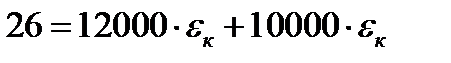
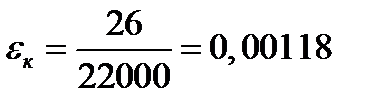
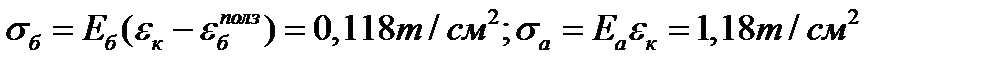
2 шаг: t=0,5 год, Δt=0,5 год

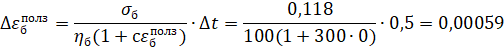
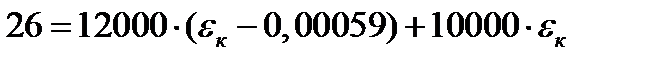
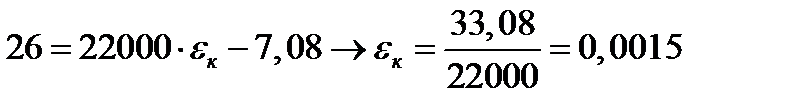
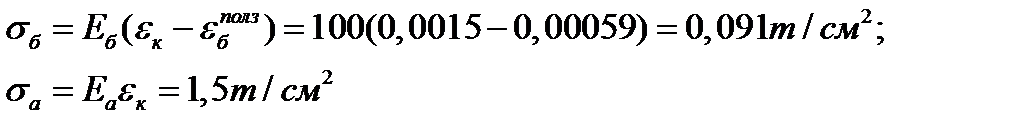
3 шаг: t=1 год, Δt=0,5 год

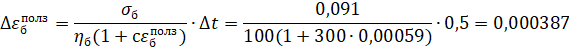
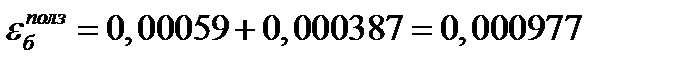
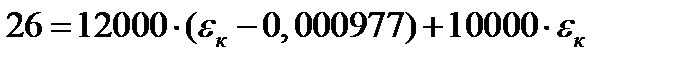
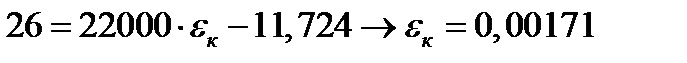
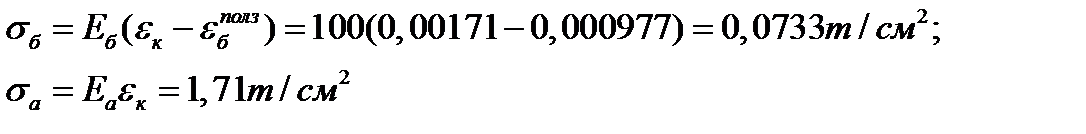
Ответ: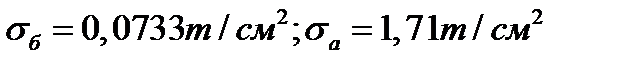

Задача №2

Р

Р

Дано: А_б=0,12м², А_а=0,01м², Р=0,13МН, Е_б=1000 МН/м²,

А Е_а=10000 МН/м², η_б=10³ МНгод/м², В=0,05 1/(МНгод/ м²),

Δt=0,5 год

2А Закон ползучести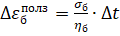

Закон накопления повреждений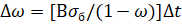

Найти: потерю ресурса в третьей

А нижней части через 1 год

Решение: Уравнение равновесия нижней части:

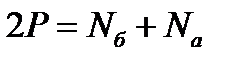
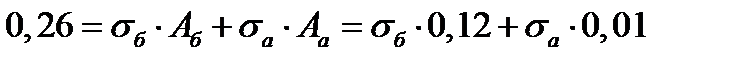
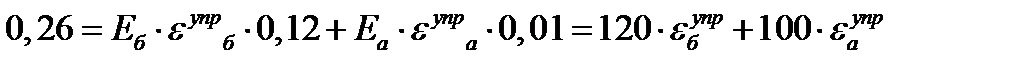
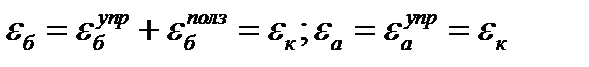
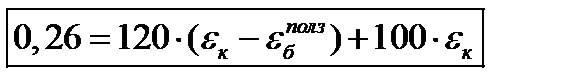
1 шаг: t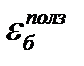=0: =0,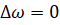

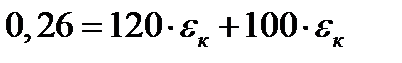
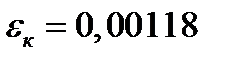
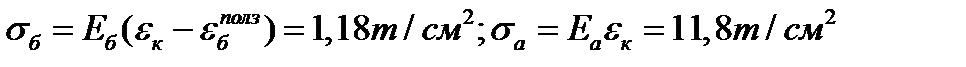
2 шаг: t=0,5 год, Δt=0,5 год

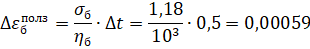
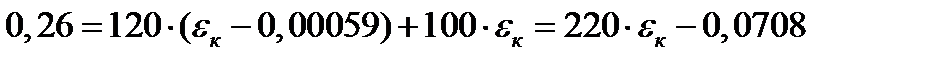
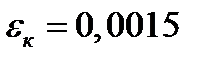
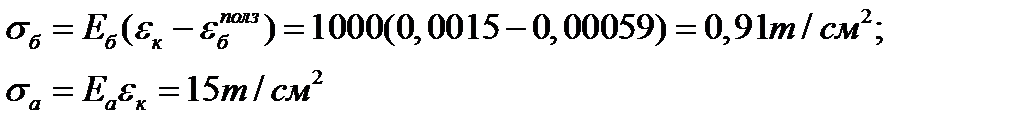
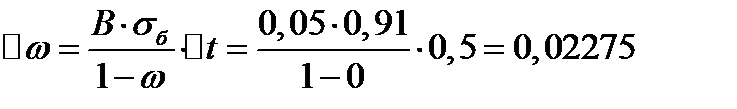
3 шаг: t=1 год, Δt=0,5 год

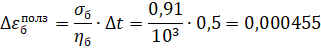
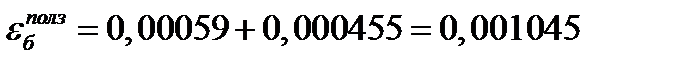
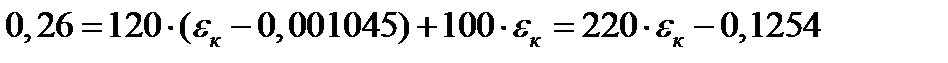
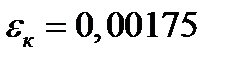
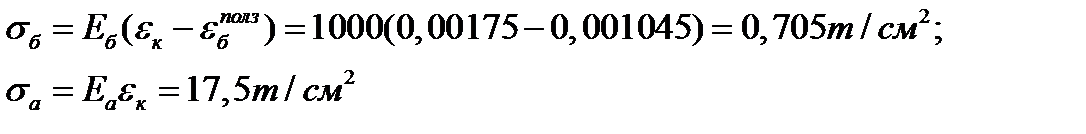
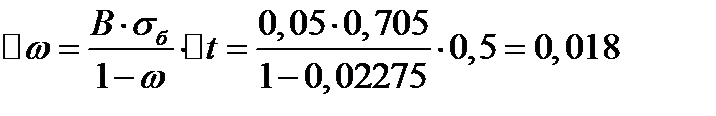
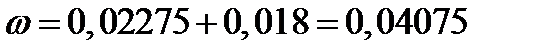
Ответ: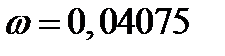

Задача №3

Для заданной схемы балки (а = 1 м, Р = 10 МН, М = 10 МНм):

1. Определить реакции опор.

2. По участкам построить эпюры Q_y и М_х и проверить прочность стеклопластикового двутавра

3. Найти критическое время c учетом перепадов температуры по временам года (ΔТ₁=262К⁰, ΔТ₂=282К⁰, ΔТ₃=308К⁰, ΔТ₄=254К⁰)

по линейной теории накопления повреждений. Критическое время определять с помощью формулы Журкова .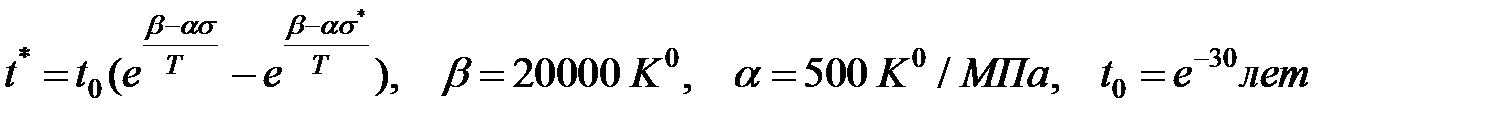

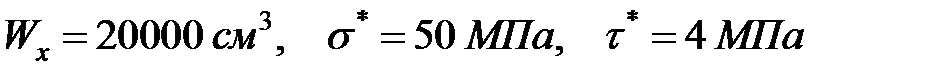
4. Найти критическое время по среднегодовой температуре

а

2а

2а

Р

М

Решение:

1. Определяем реакции опор:

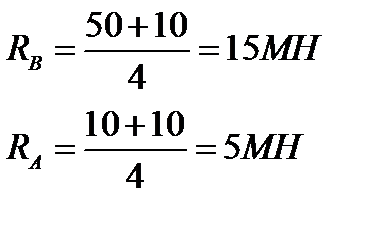
2. Эпюры Q_y и M_x

+

Q_y

-

M_x

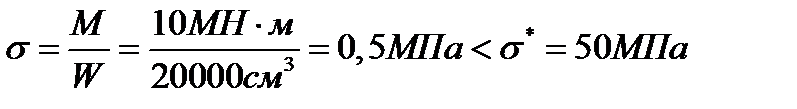
3. Критическое время по временам года:

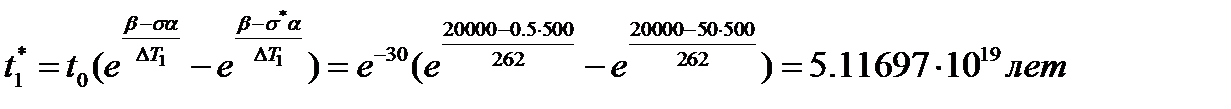
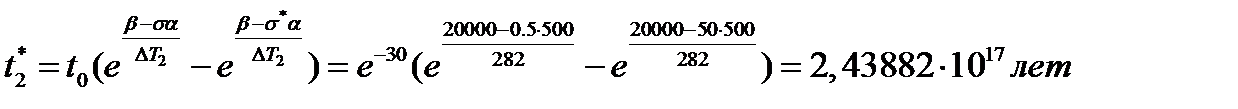
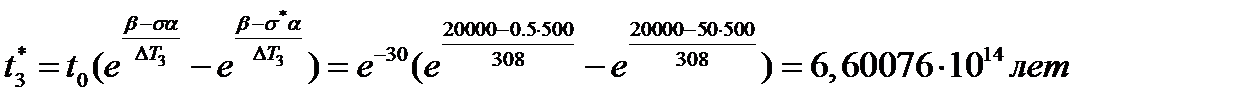
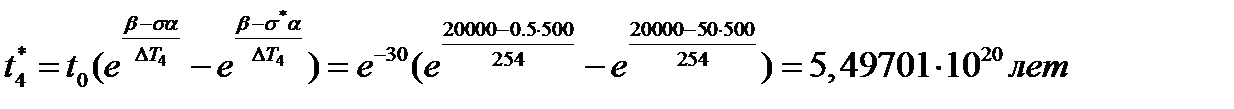
4. Накопление повреждений

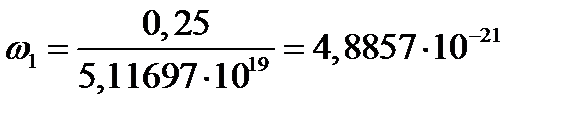
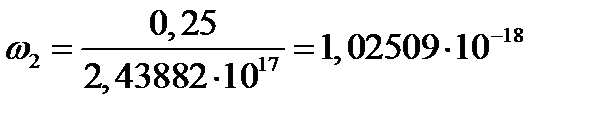
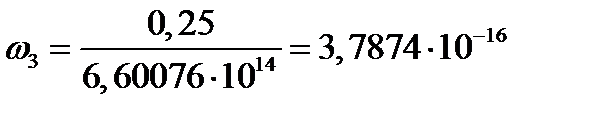
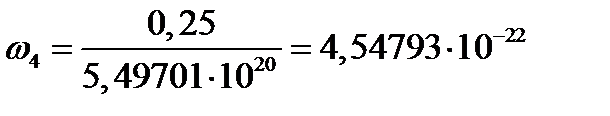
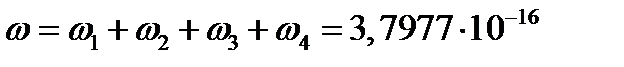
5. Критическое время

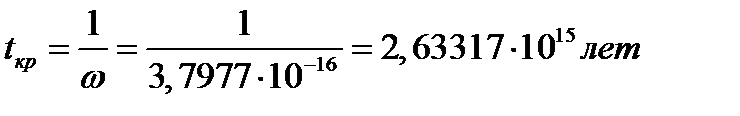
Ответ: