Реономное поведение материалов
Особенности ползучести
Моделирование ползучести играет важную роль в расчетах на прочность, особенно при повышенных температурах. Например, к некоторым элементам конструкции ядерного реактора прикладывают нагрузки, чтобы предотвратить движение соседних элементов. Однако после некоторого времени, проведенного под нагрузкой при повышенной температуре, напряжения в этих элементах конструкции релаксируют и возникает потенциальная возможность того, что эти элементы конструкции прекратят выполнять свою функцию, и соседние элементы конструкции начнут движение, что представляет потенциальную угрозу безопасности.
Исторически под явлением ползучести понимают процесснарастания во времени деформаций тела, нагруженного постоянными нагрузками. С математической точки зрения это означает,что определяющие соотношения материала содержат время явно или посредством некоторых операторов. Полная деформация 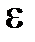 при ползучести складывается из упругой
при ползучести складывается из упругой 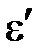 и неупругой
и неупругой 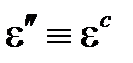 составляющей, где последняя представляет деформацию ползучести
составляющей, где последняя представляет деформацию ползучести
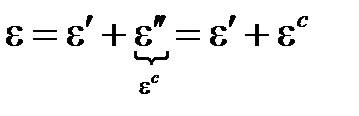 .
.
Свойство ползучести обнаруживают материалы различной природы: металлы, пластмассы,бетон, горные породы, армированные пластики, дерево, лед, органические биоматериалы и др. Однако физические механизмы ползучести у перечисленных материалов совершенно различны. Более глубокое изучение показывает, что и внешние формыпротекания ползучести сходны лишь на первый взгляд, различные материалы требуют различных средств феноменологического описания.
 |
| Рис.1.1.1 |
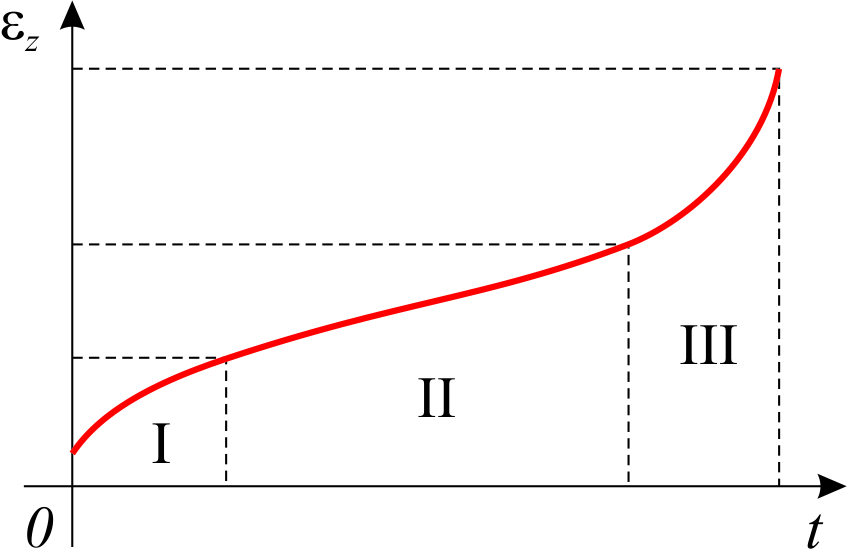
Процесс ползучести условно делят на три стадии:
1 – неустановившаяся ползучесть;
2 – установившаяся ползучесть;
3 – ускоренная (прогрессирующая) ползучесть.
В первой стадии скорость ползучести постепенно уменьшается, что связано с преобладанием механического упрочнения над термическим разупрочнением (Бейли).
Во второй стадии между механическим упрочнением и термическим разупрочнением устанавливается равновесие и процесс ползучести протекает с минимальной, постоянной во времени скоростью, которая зависит от напряжения и температуры. Наиболее популярной зависимостью скорости ползучести от напряжения при заданной температуре является степенной закон Нортона-Бейли
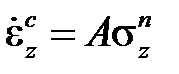 ,
,
где Aи n – это константы материала. Он хорошо согласуется с экспериментами и удобен в расчетах. Кроме тогоего легко использовать при обработке экспериментальных данных,поскольку в логарифмических координатах он представляет собой прямую линейную функцию констант материала lgAи n.
Располагая серией кривых ползучести при заданной температуре и различных напряжениях, константы материала Aи nопределяют следующим образом. Сначала определяют скорости установившейся ползучести при различных напряжениях. Затем результаты изображают в виде точек в логарифмических координатахи аппроксимируют их линейной функцией
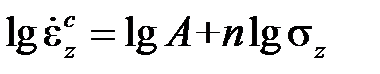 ,
,
как показано на рис.1.2.После этого на полученной прямой выбирают произвольно две точки с координатами 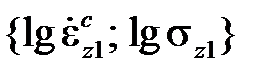 и
и 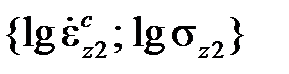 соответственно. В результате имеем
соответственно. В результате имеем
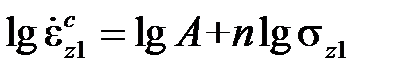 ,
, 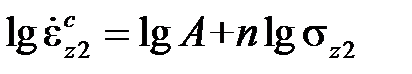 ,
,
откуда следует
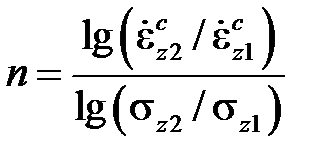 ,
, 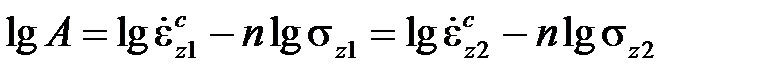 .
.
| а) Семейство кривых ползучести при фиксированной температуре | б) График зависимости логарифма напряжения от логарифма скорости установившейся ползучести |
| Рис.1.1.1.Определение констант материала для закона Нортона-Бейли |
В третьей стадии скорость ползучести возрастает до разрушения образца. Ранее предполагалось, что увеличение скорости деформацииползучести в этой стадии вызвано повышением напряжения, которое, в свою очередь, обусловлено уменьшением площади поперечного сечения образца из-за образования шейки (опыты Эндрейда). Однако позже было показано, что третья стадия не всегда соответствует образованию и развитию шейки. В случае отсутствия шейки увеличение скорости ползучести объясняется образованием местных трещин внутри образца, которые развиваются в материале в течение времени под влиянием напряжений и температуры, ослабляя образец.
 |
| Рис.1.1.2 |
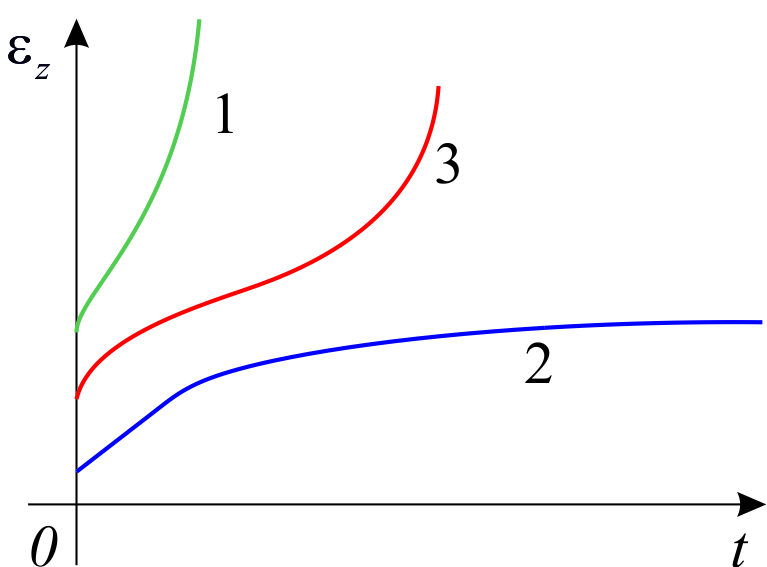
В результате экспериментов выявлены следующие особенности реологического поведения материалов.
1. При высоких температурах и напряжениях реализуется кратковременная (минутная или секундная) ползучесть(линия 1 на рис.1.1). Стадия I, характеризующая убывание скорости пластической деформации,при этом может отсутствовать. В некоторых случаях отсутствует и стадия II: скорость деформации сразу же после нагружения возрастает до разрушения.
2. При низком уровне напряжений стадия установившейся ползучести может распространяться на очень большую длительность – более 30–80 тыс. часов.
3. При низких температурах ползучесть часто ограничена I стадией, после которой скорость ползучести практически становится равна нулю (ограниченная ползучесть). Такой характер ползучести обнаруживается, например, при испытании жаропрочных сплавов при 20ᵒC, α – титановых сплавов при 350ᵒC и никелевых сплавов при 20ᵒC –400ᵒC(линия 2 на рис.1.1).
4. При высоких напряжениях стадия неустановившейся ползучести Iиногда переходит сразу в стадию ускоренной ползучести III(линия 3 на рис.1.1).
Основная задача теорий ползучести состоит в том, чтобысвязать измеряемые величины (напряжения, деформации, температуру и время) с помощью некоторого уравнения или системы уравнений, носящих универсальный характер, то есть справедливых как при постоянных, так и переменных напряжениях. Приэтом в уравнениях, вообще говоря, могут фигурировать скрытые параметры, характеризующие состояние материала. Но припостроении математических теорий ползучести мы должны постулировать принципиальную возможность существования такихуравнений, из которых внутренние параметры должны быть исключены, а все характеристики ползучести могут быть найденыв результатеэксперимента, то есть путем измерения сил и перемещений.Под простейшими теориями ползучести будем понимать такиетеории, которые черпают все необходимые данные из опытов наползучесть при постоянном напряжении.
При построении теорий ползучести исходят из следующих предположений:
1) температура в процессе ползучести не изменяется;
2) отсутствует третья стадия ползучести;
3) отсутствует мгновенная пластическая деформация, еслиэто не оговорено дополнительно.
Пример. На примере системы трех стержней одинаковой длины l, одинаковой площадью поперечного сеченияSи из одинакового материала, нагруженных силой P (рис.1.3) проиллюстрируем разницу между упругостью, пластичностью и чистой ползучестью.
| Рис.1.1.3 |
Уравнение равновесия (статика) для рассматриваемой конструкции имеет вид
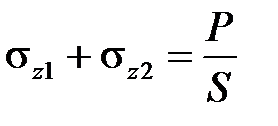 ,
,
где σz1и σz2 – напряжения соответственно в первом (или третьем) и втором стержне, а условие совместности деформаций (геометрия)
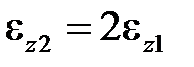 ,
,
где ez1и ez2 – продольные деформации соответственно в первом (или третьем) и втором стержне. Физические законы зависят от модели материала.
а) Рассмотрим идеально упругое поведение материала (физика):
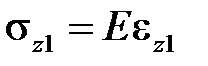 ,
, 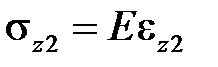 .
.
Подставим последние выражения в уравнение равновесия и с учетом условия совместности деформаций получим:
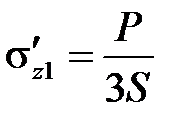 ,
, 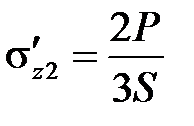 .
.
б) При использовании модели идеальной пластичности напряжения в чисто пластическом состоянии конструкции напряжения в стержнях одинаковы (равны пределу текучести) и, согласно уравнению равновесия, равны следующему
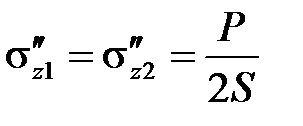 .
.
в) При чистой установившейся ползучести реономного материала примем зависимость скорости ползучести от напряжения в форме закона Нортона-Бейли. Подставляя в условие совместности деформаций, продифференцированное по времени, скорости ползучести получим
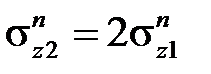 .
.
Подставим этот результат в уравнения равновесия
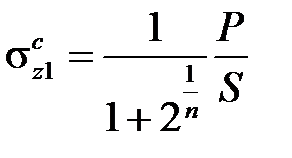 ,
, 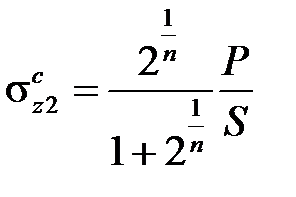 .
.
Заметим, что при n = 1 получаем величины напряжений в пределах упругости, а при n = ∞ значения напряжений в чисто пластическом состоянии.
При нестационарной ползучести, когда в процессе нагружения меняются и деформации и напряжения, обычно напряжения с течением времени изменяются от начального упругого состояния до состояния установившейся ползучести, которое достигается весьма быстро. Таким образом, поскольку расчеты с допущением установившейся ползучести значительно проще, чем без него, можно, если срок службы детали достаточно велик, использовать предположение установившейся ползучести. Однако в тех случаях, когда необходимо исследовать изменение и перераспределение напряжений во времени, как, например, в задаче о релаксации контактного давления в диске, посаженного на вал с натягом, предположение установившейся ползучести не может быть принято.
Кратковременная ползучесть
При решении практических задач приходится иметь дело с изделиями, предназначенными для самых разнообразных длительностей службы. Узлы паровых турбин проектируются в расчете на длительность службы, измеряемую годами и даже десятками лет, а для элементов ракетных двигателей требуется гарантировать прочность при действии нагрузок и температур в течение нескольких минут или даже секунд. В первом случае нагрузки и температуры должны быть относительно невысоки, во втором можно допустить значительные нагрузки при высоких температурах. Поведение материала в этих случаях существенно отличается.
Области ползучести условно делят на три диапазона:
o Длительная ползучесть (месяцы, годы);
o Ползучесть средней длительности (часы, дни);
o Кратковременная ползучесть (секунды, минуты).
Часто длительную ползучесть и ползучесть средней длительности не различают, а кратковременной называют ползучесть, происходящую в таких условиях, когда за время, не превышающее 20-30 мин, накапливается деформация ползучести либо сравнимая по величине с мгновенной деформацией, либо превышающая ее. Приведенное определение по существу характеризует не столько длительность процесса, сколько рабочие диапазоны напряжений и температур, поскольку фиксация точных границ для деформации и времени службы затруднительна.
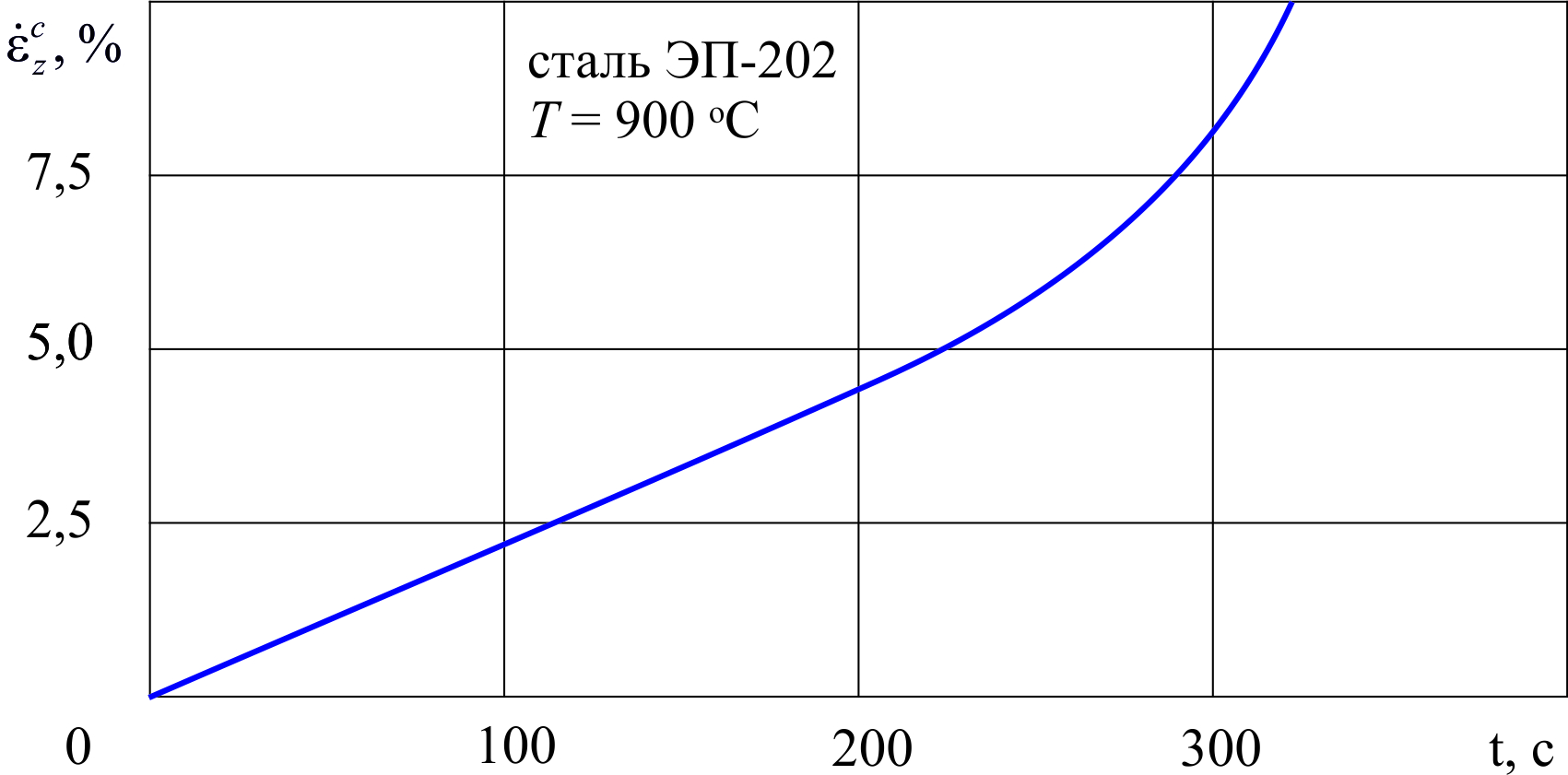 |
| Рис.1.2.1 |
Отметим некоторые особенности кратковременной ползучести на примере на примере стали ЭП-22 при температуре 900 ᵒС при напряжении 30-40 кг/мм2 (рис.1.2.1):
o Первый участок на кривой отсутствует и с самого начала ползучесть протекает с постоянной скоростью;
o При малых деформациях (порядка 1-2%) скорость ползучести зависит только от текущих значений напряжения и температуры и не зависит от предыстории;
o Анизотропия материала не играет существенно роли (при умеренных температурах и напряжениях скорость ползучести существенно зависит от текстуры материала);
o Разрушение образцов при кратковременной ползучести, как правило, происходит при постоянной величине равномерного удлинения, то есть не зависит от температуры и напряжения. Разрушению предшествует появление третьих участков на кривых ползучести. Разрушение не связано с изменением площади поперечного сечения и происходит вследствие развития трещин по границам зерен.
Отмеченные особенности протекания процесса кратковременной ползучести позволяют описывать ее следующим уравнением
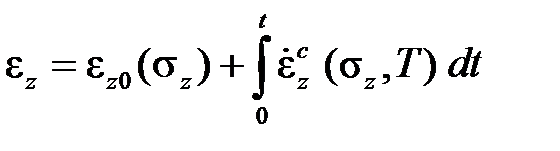 ,
, 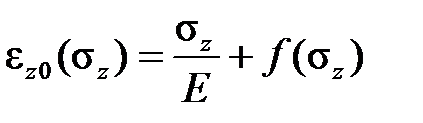 ,
,
где 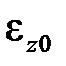 – это мгновенная упругопластическая деформация, определяемая диаграммой мгновенного растяжения. То же самое можно записать в скоростях, подставив в предыдущее выражение зависимости скоростей деформаций от напряжений
– это мгновенная упругопластическая деформация, определяемая диаграммой мгновенного растяжения. То же самое можно записать в скоростях, подставив в предыдущее выражение зависимости скоростей деформаций от напряжений
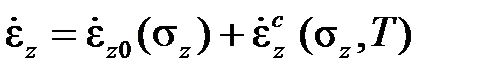 ,
, 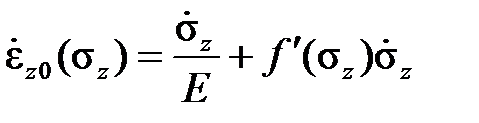 .
.
Здесь 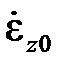 – этоскорость мгновенной упругопластической деформации, а
– этоскорость мгновенной упругопластической деформации, а 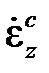 – скорость деформации ползучести. Приведенные выше особенности кратковременной ползучести наблюдаются не у всех материалов. Медь и некоторые медные сплавы, например, при любых напряжениях и температурах обнаруживают участок неустановившейся ползучести.
– скорость деформации ползучести. Приведенные выше особенности кратковременной ползучести наблюдаются не у всех материалов. Медь и некоторые медные сплавы, например, при любых напряжениях и температурах обнаруживают участок неустановившейся ползучести.
Для практических расчетов скорость деформации ползучести скорость деформации ползучести нужно представить в некоторой аналитической форме. Неизбежный разброс экспериментальных данных делает приемлемыми различные аналитические аппроксимации закона ползучести, и при выборе той или иной аппроксимации можно руководствоваться соображениями удобства ее применения в расчетах.
Для описания кратковременной ползучести в большинстве случаев используют две зависимости: экспоненциальную и степенную (Нортон-Бейли).Экспоненциальная зависимость
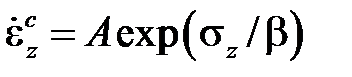 ,
,
где Aи β – это константы материала при данной температуре, непригодна для малых напряжений, так как при напряжении 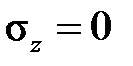 скорость ползучести отлична от нуля. Правда, поскольку при расчетах на прочность область малых напряжений не представляет интереса, формулой можно пользоваться, принимая соответствующие меры к тому, чтобы избежать формальных противоречий в точках, где напряжение равно нулю. Степенная зависимость
скорость ползучести отлична от нуля. Правда, поскольку при расчетах на прочность область малых напряжений не представляет интереса, формулой можно пользоваться, принимая соответствующие меры к тому, чтобы избежать формальных противоречий в точках, где напряжение равно нулю. Степенная зависимость
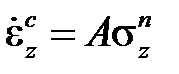 ,
,
где Aи n – это константы материала при данной температуре,более популярна. Зависимость констант ползучести от температуры обычно задается графически или в виде таблиц.
Для кратковременной ползучести имеет большое значение точность определения мгновенных характеристик материала. Мгновенной кривой деформирования материалабудем называть диаграмму, снятую с такой скорость, при которой влияние сопутствующей деформированию ползучести несущественно (не следует путать эту кривую с динамической кривой, получаемой при больших скоростях деформирования. Для построения мгновенной кривой деформирования рекомендуется следующая методика. Проводится серия испытаний на одноосное растяжениес постоянной скоростью изменения напряжения
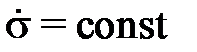 .
.
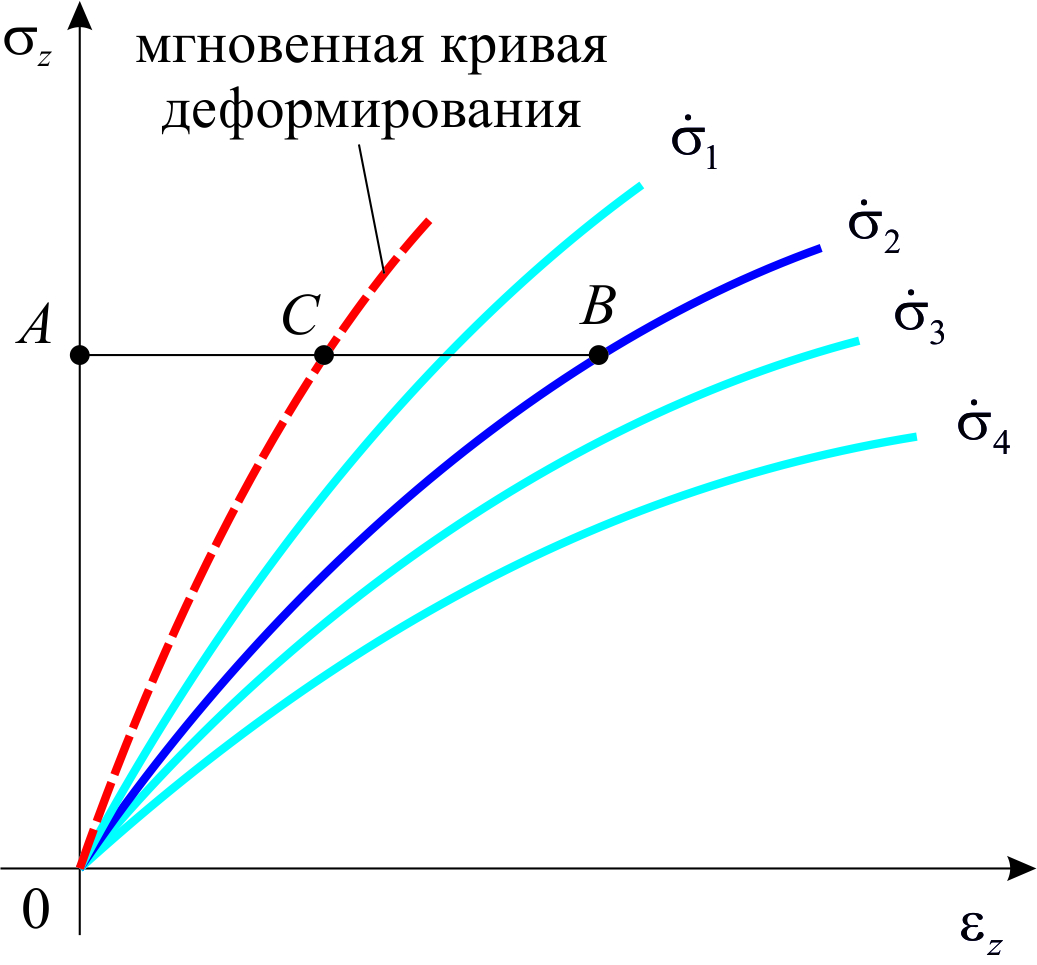 |
| Рис.1.2.2 |
На рис. 1.2.2 схематично показаны такие кривые для разных значений 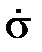 , причем
, причем 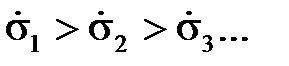 . Рассмотрим одну из этих кривых, например, кривую, соответствующую скорости нагружения
. Рассмотрим одну из этих кривых, например, кривую, соответствующую скорости нагружения 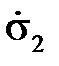 . Абсцисса ABнекоторой точки Bэтой кривой к моменту, когда напряжение достигло величины σ, представляет собой полную деформацию e, состоящую из мгновенной упругопластической деформации ACи деформации ползучести CB.Заметим, что эта ползучесть имеет место не при постоянном, а при переменном напряжении
. Абсцисса ABнекоторой точки Bэтой кривой к моменту, когда напряжение достигло величины σ, представляет собой полную деформацию e, состоящую из мгновенной упругопластической деформации ACи деформации ползучести CB.Заметим, что эта ползучесть имеет место не при постоянном, а при переменном напряжении 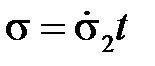 . Предположим теперь, что из независимых опытов на чистую ползучесть (то есть ползучесть при постоянном напряжении) найдено соотношение, определяющее скорость деформации ползучести. Проинтегрировав его при напряжении
. Предположим теперь, что из независимых опытов на чистую ползучесть (то есть ползучесть при постоянном напряжении) найдено соотношение, определяющее скорость деформации ползучести. Проинтегрировав его при напряжении 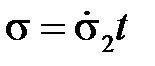 , получаем величину CBи, тем самым, находим положение точки C, принадлежащей мгновенной диаграмме деформирования. Например, при выборе закона Нортона-Бейли получим
, получаем величину CBи, тем самым, находим положение точки C, принадлежащей мгновенной диаграмме деформирования. Например, при выборе закона Нортона-Бейли получим
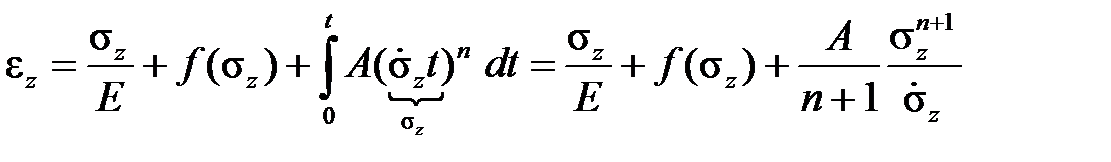 .
.
Оказывается, что обрабатывая подобным образом кривые растяжения, снятые даже с сильно разнящимися скоростями нагружения (на 3–4 порядка), получим одну и ту же кривую мгновенного деформирования с точностью до разброса свойств материала образцов.
Очевидно, что чем больше скорость нагружения, тем меньше сказывается ползучесть и тем ближе опытная кривая к полученной путем пересчета кривой мгновенного деформирования. Если температура испытания не слишком высока, то кривая растяжения, снятая за 1-2 секунды ( 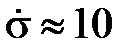 кг/мм2·с), для многих материалов может быть принята за мгновенную кривую.
кг/мм2·с), для многих материалов может быть принята за мгновенную кривую.
Пределы ползучести
Кривые ползучести являются основой расчета на ползучесть. Для сопоставления сопротивления различных материалов ползучести вводится условная характеристика – условный предел ползучести[σпл]. Будем различать условный предел ползучести по допускаемой деформации и условный предел ползучести по допускаемой скорости установившейся ползучести. Вторая формулировка используется, как правило, для деталей, работающих длительный срок.
Под условным пределом ползучестипо допускаемой деформации будем понимать напряжение[σпл], при котором деформация ползучести за заданный промежуток времени tслдостигает величины допускаемой деформации [e], установленной техническими условиями. Из приведенного определения следует, что для данного материала предел ползучести зависит от температуры и времени испытания, а также и от принятой величины допускаемой деформации. Заданный промежуток времени 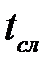 обычно принимается равным сроку службы детали. Допускаемая деформация[e] выбирается обычно, исходя из условий нормальной эксплуатации детали за срок ее службыtсл. Ориентировочные данные о величинах суммарной допускаемой деформации ползучести[e]для некоторых элементов конструкций приведены в таблице 1.3.1.
обычно принимается равным сроку службы детали. Допускаемая деформация[e] выбирается обычно, исходя из условий нормальной эксплуатации детали за срок ее службыtсл. Ориентировочные данные о величинах суммарной допускаемой деформации ползучести[e]для некоторых элементов конструкций приведены в таблице 1.3.1.
Таблица 1.3.1
| Элемент конструкции | Срок службы, ч | [e] |
| Турбинные диски | 105 | 0,0001 |
| Паропроводы | 105 | 0,003 |
| Цилиндры паровых турбин | 105 | 0,001 |
Условный предел ползучести [σпл]по допускаемой деформации определяют следующим методом. На графиках семейства кривых ползучести при различных напряжениях проводят вертикаль на расстоянии tсл от начала координат, и установив зависимость напряжения от деформации ползучести для выбранного значения времени строят соответствующий график. По этому графику и находят величину предела ползучести как ординату точки, абсцисса которой равна[e].Расчетное условие в рассматриваемом случае имеет вид
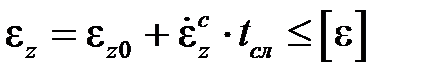 .
.
Пренебрегая стадией неустановившейся ползучести и вводя степенной закон для скорости установившейсяползучести, для определения условного предела ползучести по допускаемой деформации получим
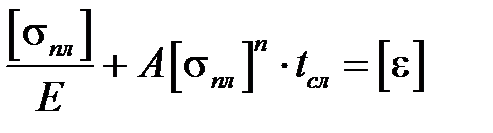 .
.
| Семейство кривых ползучести | Мгновенная кривая деформирования для значения времени t= tсл |
В случае, когда и начальная деформация, и деформация в стадии неустановившейся ползучести малы сравнительно с деформацией ползучести в установившейся стадии, при определении предела ползучести исходят из наибольшей допускаемой скорости деформации установившейся ползучести. Под условным пределом ползучести по допускаемой скорости деформации установившейся ползучести 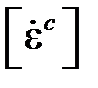 будем понимать напряжение, при котором скорость деформации ползучести равна определенной величине, установленной техническими условиями. Величина предела ползучести в таком определении зависит от от температуры и принятой величины скорости деформации. Ориентировочные данные о значениях
будем понимать напряжение, при котором скорость деформации ползучести равна определенной величине, установленной техническими условиями. Величина предела ползучести в таком определении зависит от от температуры и принятой величины скорости деформации. Ориентировочные данные о значениях 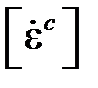 для некоторых элементов конструкций приведены в таблице 1.3.2.
для некоторых элементов конструкций приведены в таблице 1.3.2.
| Семейство кривых ползучести | График зависимости логарифма напряжения от логарифма скорости установившейся ползучести |
Таблица 1.3.2
| Элемент конструкции | 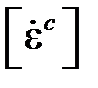 , 1/ч , 1/ч |
| Турбинные диски | 10–9 |
| Паропроводы | 10–8 |
| Цилиндры паровых турбин | 10–6 – 10–5 |
Для определения предела ползучести по допускаемой скорости ползучести вначале при помощи кривых ползучести устанавливают значения скорости установившейся ползучести при различных напряжениях. Затем в логарифмических координатах строят график зависимости логарифма напряжения от логарифма скорости установившейся ползучести, который представляет прямую линию. По этому графику и находят величину предела ползучести.
При степенном законе для скорости установившейся ползучести расчетное условие имеет вид
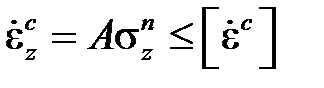 .
.
Для определения условного предела ползучести по допускаемой скорости деформации установившейся ползучести получаем
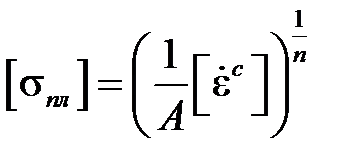 .
.
Длительная прочность
В теории ползучести дополнительно вводится понятие о длительной прочности, как о напряжении, вызывающем разрушение за заданный срок службы. Пределом длительной прочностиσдл называют отношение нагрузки, при которой происходит разрушение растянутого образца через определенный промежуток времени, к первоначальной площади его поперечного сечения. Таким образом, предел длительной прочности зависит от температуры испытания и отрезка времени до момента разрушения, который обычно выбирают, равным сроку службы детали tсл.
При исследовании длительной прочности материала испытывают несколько одинаковых образцов при различных напряжениях и устанавливают время, необходимое для разрушения каждого образца. По результатам испытаний строят соответствующий график (предел длительной прочности – время до разрушения) и по нему определяют предел длительной прочности для заданного времени.
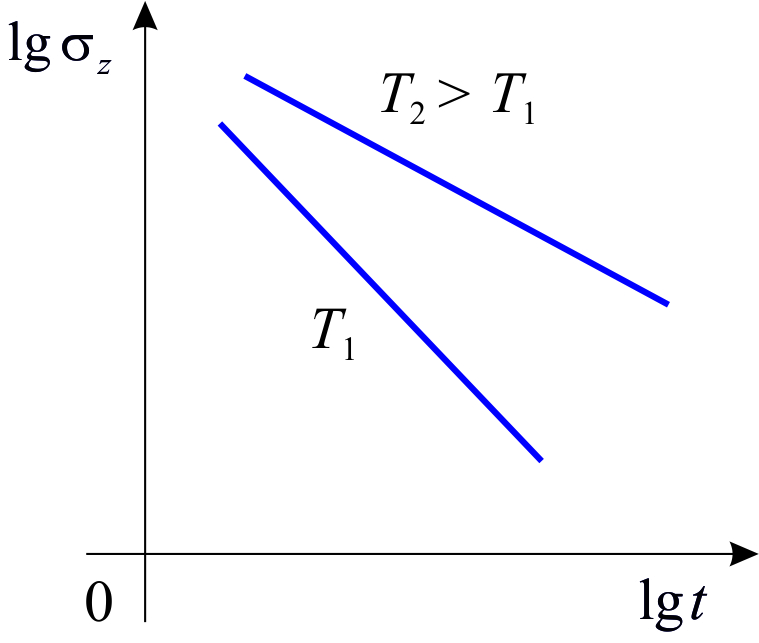
Обычно зависимость предела длительной прочности от времени до разрушения при данной температуре представляется графически в логарифмических координатах 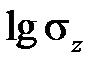 –
– 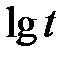 (рис.1.3.1). С увеличением температуры (рис.1.3.1а) и заданного промежутка времени до разрушения, величина предела длительной прочности снижается. Перелом на кривой длительной прочности (рис.1.3.1б) обычно наблюдается при достаточно длительных испытаниях и соответствует переходу от вязкого разрушения с образованием шейки к хрупкому без образования шейки.
(рис.1.3.1). С увеличением температуры (рис.1.3.1а) и заданного промежутка времени до разрушения, величина предела длительной прочности снижается. Перелом на кривой длительной прочности (рис.1.3.1б) обычно наблюдается при достаточно длительных испытаниях и соответствует переходу от вязкого разрушения с образованием шейки к хрупкому без образования шейки.
 | |
| а) | б) |
| Рис.1.3.1 |
Поскольку в логарифмических координатах график зависимости длительной прочности от времени является линейным, то зависимость времени до разрушения от предела длительной прочности является степенной
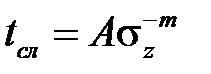 ,
,
где Aи m – это константы материала, зависящие от температуры и характера разрушения. Для того, чтобы отразить влияние на длительную прочность температуры (то есть установить так называемые температурно-временные зависимости длительной прочности), предложены различные температурно-временные параметры, являющиеся функциями предела длительной прочности. К ним относят параметр Ларсона-Миллера, Мэнсона-Хаферда и др.
Модели Максвелла и Фойгта
Первые наблюдения над ползучестью носили качественный характер. Исследователи еще тогда отметили аналогию ползучести с вязким течением жидкости и при попытке описать деформацию твердого тела во времени объединили свойства вязкости и упругости. Как известно, напряжение и скорость деформации в вязкой жидкости связаны законом вязкости Ньютона 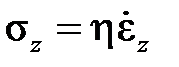 (h – коэффициент вязкости), а в упругом теле справедлив закон упругости Гука
(h – коэффициент вязкости), а в упругом теле справедлив закон упругости Гука 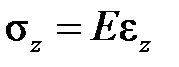 .
.
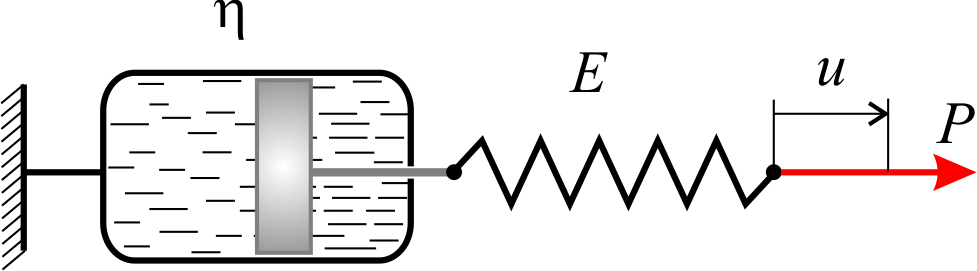
Соответствующие механические модели можно представить в виде вязкого и упругого элементов, комбинируя которые можно получить модель Максвелла (рис.2.1.1а)
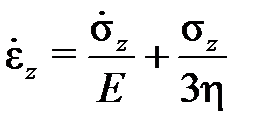
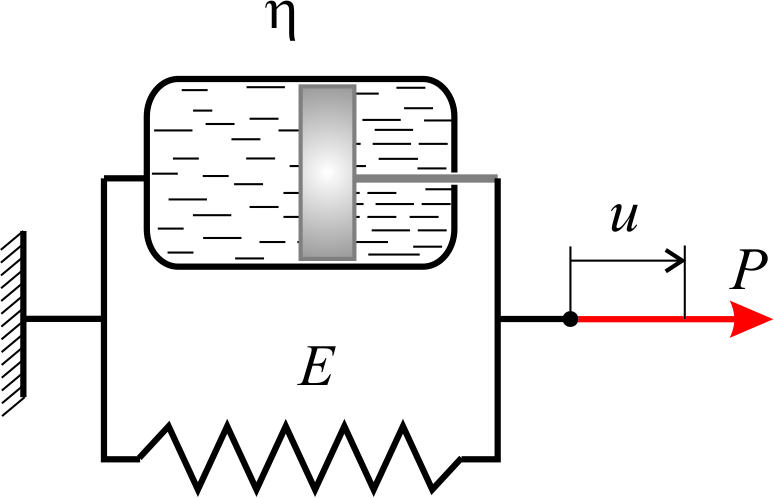
или модель Фойгта (рис.2.1.1б)
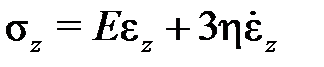 .
.
В модели Максвелла можно заметить, что если напряжение постоянно (простое последействие), то деформация возрастает неограниченно с постоянной скоростью. Если же считать постоянной деформацию, то для описания релаксации с некоторого начального напряжения 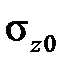 получаем уравнение
получаем уравнение
 |  |
| а) | б) |
| Рис.2.1.1 |
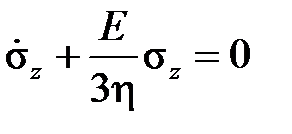 ,
,
решение которого имеет вид
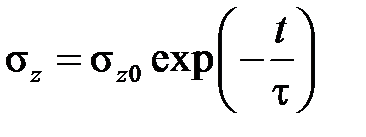 ,
, 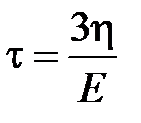 ,
,
где 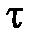 – это время релаксации.Модель Фойгта позволяет получить закон изменения деформации во времени при постоянном напряжении в виде
– это время релаксации.Модель Фойгта позволяет получить закон изменения деформации во времени при постоянном напряжении в виде
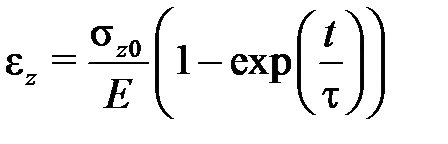 .
.
При постоянной деформации материал Фойгта не релаксирует – напряжение остается постоянным. Время 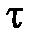 при этом называют временем запаздывания.
при этом называют временем запаздывания.
Реальные материалы, как правило, не подчиняются моделям Максвелла и Фойгта. Эти модели только качественно отражают некоторые стороны сложных процессов деформирования материалов во времени. Стремясь лучше описать эти процессы, модели иногда усложняют, соединяя три элемента (модель Кельвина), четыре и т.д. Однако это приводит к громоздким математическим решениям и все-таки не позволяет удовлетворительно описать поведение реальных материалов во времени. Поэтому в расчетах деталей машин и элементов конструкции в основном распространение получили технические теории ползучести.
