Vi. «методы решения линейных неоднородных алгебраических уравнений »
1.«Метод Крамера».
Теорема Крамера: Пусть определитель матрицы 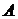 системы D, а
системы D, а 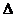 j– определители матриц, получаемых из данных заменой j-го столбца на столбец свободных членов. Тогда, если
j– определители матриц, получаемых из данных заменой j-го столбца на столбец свободных членов. Тогда, если 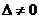 , то система имеет единственное решение, которое вычисляется по формулам КРАМЕРА:
, то система имеет единственное решение, которое вычисляется по формулам КРАМЕРА: 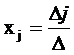 , где j=1; …;
, где j=1; …; 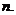
| Алгоритм метода Крамера | Пример. Решить систему уравнений методом Крамера: 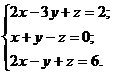 | |
1. Записать матрицу  системы и найти ее определитель D, если D = 0 , то система решений не имеет. системы и найти ее определитель D, если D = 0 , то система решений не имеет. | 1. 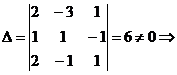 система имеет единственное решение. система имеет единственное решение. | |
2. Если 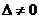 , то находим , то находим 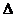 j, заменяя j-й столбец столбцом свободных членов. j, заменяя j-й столбец столбцом свободных членов. | 2. 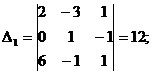 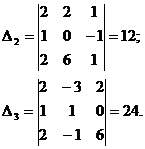 | |
3. По формулам Крамера находим х 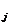 : : 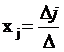 | 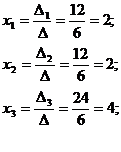 Ответ: Ответ: 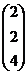 | |
2.«Матричный метод».
Если определитель матрицы  системы
системы 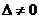 , то матрица системы невырожденная, а значит, имеет обратную матрицу
, то матрица системы невырожденная, а значит, имеет обратную матрицу 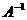 . Умножим обе части матричного равенства
. Умножим обе части матричного равенства 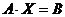 на обратную матрицу
на обратную матрицу 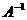 слева, получим равенство:
слева, получим равенство: 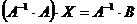 , или
, или 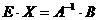 , откуда
, откуда 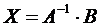 - равенство, выражающее суть матричного метода.
- равенство, выражающее суть матричного метода.
| Алгоритм матричного метода | Пример: Решить систему матричным методом. 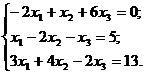 |
| 1. Записать матрицу системы и найти ее определитель. Если определитель равен нулю, то система не имеет решений. | 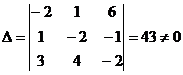 -система имеет решение, матрица системы имеет обратную. -система имеет решение, матрица системы имеет обратную. |
2. Ищем матрицу 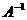 , обратную матрице , обратную матрице  системы по формуле системы по формуле 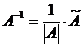 , где , где 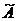 связана с связана с 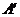 (нужно транспонировать матрицу (нужно транспонировать матрицу  ). ). | 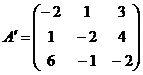 ; ; 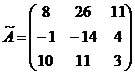 Заменяем элементы транспонированной матрицы Заменяем элементы транспонированной матрицы 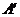 их алгебраическими дополнениями: их алгебраическими дополнениями: 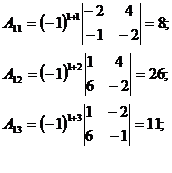 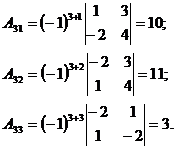 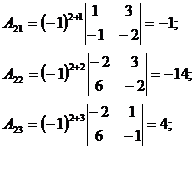 Теперь запишем Теперь запишем 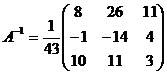 , и так и оставляем (для удобства последующих вычислений). , и так и оставляем (для удобства последующих вычислений). |
3. Ищем матрицу – столбец 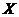 значений переменных системы по формуле значений переменных системы по формуле 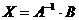 | 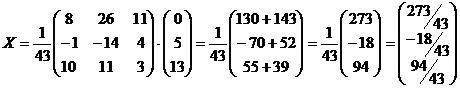 Ответ: Ответ: 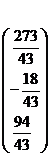 . . |
3.«Метод Гаусса».
Или метод последовательного исключения переменных - заключается в том, что с помощью элементарных преобразований данная система уравнений приводится к равносильной системе уравнений ступенчатого (треугольного) вида, из которой, последовательно, начиная с последней переменной, находятся все остальные переменные.
Системой треугольного (ступенчатого) вида называется система вида
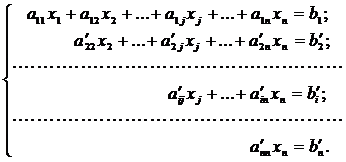
Получают такую систему с помощью следующих элементарных преобразований систем линейных неоднородных алгебраических уравнений:
1. изменение порядка уравнений системы,
2. умножение или деление обеих частей любого уравнения системы на одно и то же не равное нулю число,
3. почленное сложение уравнений системы.
Пример. Решить данную систему методом Гаусса. 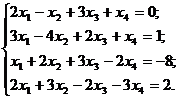 | Пояснения по ходу решения. |
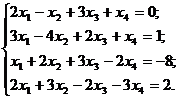 | Сделаем III-е уравнение системы I-м. |
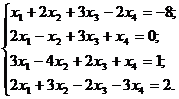 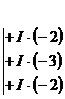 | Сделаем коэффициенты при х1 равными нулю с помощью элементарных преобразований 2. и 3. |
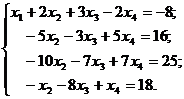 | Сделаем IV-е уравнение системы II -м. |
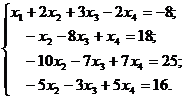 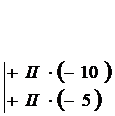 | Сделаем коэффициенты при х 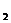 равными нулю с помощью элементарных преобразований 2. и 3. равными нулю с помощью элементарных преобразований 2. и 3. |
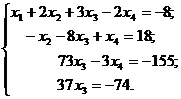 | Получили IV-е уравнение как уравнение с одной переменной, решая его, найдем значение переменной х 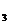 |
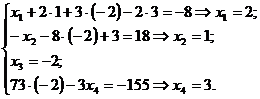 Ответ: Ответ: 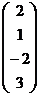 . . | Из последнего уравнения, подставляя найденное значение переменной х 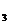 , находим значение переменной х4 , подставляем его во II уравнение и находим из этого уравнения значение переменной х , находим значение переменной х4 , подставляем его во II уравнение и находим из этого уравнения значение переменной х 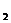 , затем с помощью подстановки в уравнение I находим значение переменной х1.Записываем ответ. , затем с помощью подстановки в уравнение I находим значение переменной х1.Записываем ответ. |
ПРИМЕР РЕШЕНИЯ СИСТЕМЫ ВСЕМИ ТРЕМЯ МЕТОДАМИ
Решить систему линейных алгебраических уравнений методами Крамера, Гаусса и матричным методом.
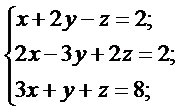
I. Метод Крамера.
Количество уравнений (3) равно количеству переменных (3), значит, матрица системы квадратная и имеет определитель.
Вычислим определитель матрицы системы:
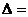
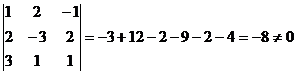 - значит, система уравнений имеет единственное решение, которое находят по формулам Крамера:
- значит, система уравнений имеет единственное решение, которое находят по формулам Крамера: 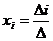 ,
, 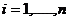 .
.
Заменяем 1–й столбец столбцом свободных членов
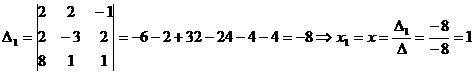
Заменяем 2-й столбец столбцом свободных членов
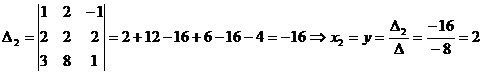
Заменяем 3-й столбец столбцом свободных членов
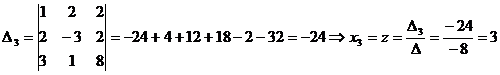
Ответ: 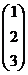 .
.
II. Матричный метод.
Данную систему уравнений можно записать в матричной форме 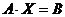 :
:
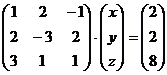 , откуда
, откуда 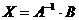 .
.
Найдем матрицу, обратную матрицу  . Так как
. Так как 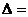
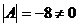 , такая матрица существует. Найдем алгебраические дополнения к элементам матрицы
, такая матрица существует. Найдем алгебраические дополнения к элементам матрицы  по формуле
по формуле 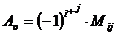 :
:
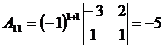 ;
; 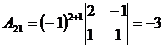 ;
; 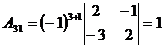 ;
;
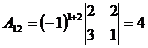 ;
; 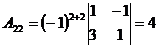 ;
; 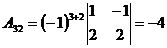 ;
;
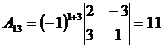 ;
; 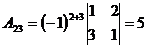 ;
; 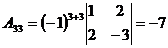 .
.
Тогда
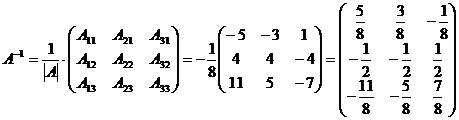 .
.
А теперь найдем решение системы:
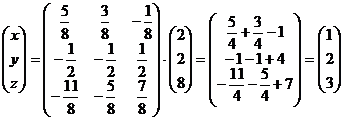 .
.
Ответ: 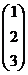 .
.
III. Метод Гаусса.
Выполним преобразования:
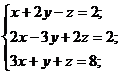
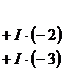 Сделаем коэффициенты при х равными нулю.
Сделаем коэффициенты при х равными нулю.
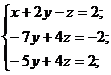
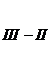 Т.к. коэффициенты при z во II и III уравнениях системы равны, то можно из III уравнения вычесть II уравнение.
Т.к. коэффициенты при z во II и III уравнениях системы равны, то можно из III уравнения вычесть II уравнение.
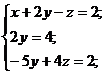 Таким образом, получили, что II уравнение системы есть уравнение с одной переменной, значит, можно вычислить значение переменной у.
Таким образом, получили, что II уравнение системы есть уравнение с одной переменной, значит, можно вычислить значение переменной у.
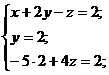 Теперь последовательно, с помощью подстановки, вычисляем значения
Теперь последовательно, с помощью подстановки, вычисляем значения
переменных z и х.
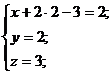
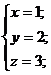
Ответ: 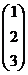 .
.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
v Необходимые условия применения метода Крамера:
a. Количество уравнений системы должно равняться количеству неизвестных.
b. Определитель основной матрицы системы не должен равняться нулю: 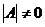 .
.
Решение по правилу Крамера находят по формулам:
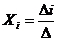 , где
, где 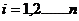 , где
, где 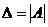 ,
,
а 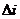 - определитель, который получается из основного определителя матрицы
- определитель, который получается из основного определителя матрицы  заменой
заменой 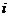 - го столбца столбцом свободных членов системы.
- го столбца столбцом свободных членов системы.
v При решении системы матричным способом сначала надо найти 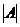 . Система имеет решение при условии
. Система имеет решение при условии 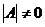 . Затем ищут обратную матрицу к матрицу
. Затем ищут обратную матрицу к матрицу  :
: 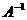 . После этого умножают
. После этого умножают 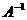 на матрицу – столбец свободных членов системы:
на матрицу – столбец свободных членов системы: 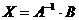
Полученная при этом матрица-столбец и является решением системы.
v Метод Гаусса состоит в приведении системы к треугольному виду. Для системы, состоящей из 3-х уравнений с 3-мя неизвестными метод Гаусса выглядит так: исключаем 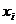 из 2-го и 3-го уравнений системы: затем исключаем
из 2-го и 3-го уравнений системы: затем исключаем 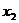 из 3-го уравнения и решаем полученную систему.
из 3-го уравнения и решаем полученную систему.
Решить каждую систему линейных алгебраических уравнений всеми тремя
способами:
1) 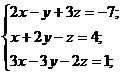 2)
2) 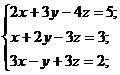 3)
3) 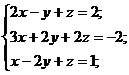
4) 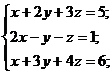 5)
5) 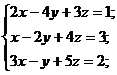 6)
6) 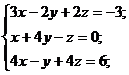
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Операции над матрицами.
1.1. Что такое матрица?
1.2. Какие виды матриц Вы знаете?
1.3. Что означает размер матрицы m?n?
1.4. Какую матрицу называют квадратной?
1.5. Какие две матрицы можно сложить?
1.6. Когда две матрицы можно перемножить?
1.7. Матрицу какого вида можно возвести в степень?
1.8. В чем суть транспонирования матрицы?
1.9. При транспонировании размер матрицы не изменился. Матрицу какого вида транспонировали?
2. Свойства определителей.
2.1. Что можно сказать об определителе матрицы, у которой:
2.1.1 одна строка содержит только нулевые элементы;
2.1.2 элементы двух столбцов равны;
2.1.3 элементы двух строк пропорциональны;
2.1.4 две строки матрицы поменяли местами;
2.1.5 к элементам одного столба прибавили соответствующие элементы другого столбца, умноженные на одно и то же число.
2.2. Сравните определители матрицы  и матрицы
и матрицы 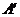 , транспонированной по отношению к матрице
, транспонированной по отношению к матрице  .
.
2.3. Как вычисляют определители квадратных матриц:
2.3.1 второго порядка;
2.3.2 третьего порядка;
2.3.3 четвертого порядка
2.4. Чем матрица отличается от определителя матрицы?
3. Ранг матрицы.
3.1. Что такое ранг матрицы?
3.2. Как проще вычислить ранг матрицы? Какие элементарные преобразования матриц при этом применяются?
4. Обратная матрица.
4.1. Какую матрицу называют обратной?
4.2. Для какой матрицы существует обратная?
4.3. Какой вид имеет обратная матрица?
4.4. Сформулируйте теорему об обратной матрице.
4.5. Перечислите этапы нахождения элементов обратной матрицы.
5. Метод Крамера.
5.1. Сформулируйте теорему Крамера и запишите формулы Крамера.
5.2. Перечислите этапы решения системы неоднородных линейных уравнений методом Крамера.
5.3. Для каких систем уравнений (количество уравнений и переменных в них) применим метод Крамера?
6. Метод Гаусса.
6.1. В чем суть метода Гаусса?
6.2. Что применяют для получения треугольной (ступенчатой) системы уравнений?
6.3. Для каких систем уравнений (количество уравнений и переменных в них) применим метод Гаусса?
7. Матричный метод.
7.1. В чем суть матричного метода?
7.2. Для каких систем уравнений (количество уравнений и переменных в них) применим матричный метод?
7.3. Матрицу какого вида используют для решения системы матричным методом?
7.4. Какое равенство используют для решения системы матричным методом?
ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ
Вариант I
1. Данная запись есть
а) Матрица размера mxn;
б) Определитель 3го порядка;
в) Матрица 4го порядка.
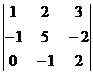
2. Если элементы двух строк матрицы пропорциональны, то ее определитель равен:
а) 1;
б) 0;
в) -1
3. Данная матрица есть
а) Диагональная;
б) Матрица-строка;
в) Нулевая.
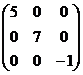
4. Данные формулы есть формулы для решения систем уравнения по:
а) Методу Крамера;
б) Методу Гаусса;
в) Матричному методу.
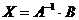
5. Обратная матрица 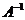 не существует, если:
не существует, если:
а) 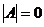 ;
;
б) 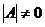 ;
;
в) 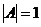 .
.
6. Матрица  и
и 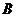 можно сложить, если
можно сложить, если
а)  - матрица строка,
- матрица строка, 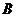 - матрица столбец;
- матрица столбец;
б)  и
и 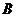 одинокого размера;
одинокого размера;
в)  - нулевая матрица размера
- нулевая матрица размера 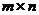 ,
, 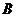 - диагональная
- диагональная 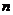 - порядка.
- порядка.
7. Возвести матрицу в степень
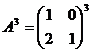
Ответ: а) 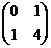 ; б)
; б) 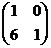 ; в)
; в) 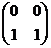 .
.
8. Посчитать определитель по теореме Лапласа:
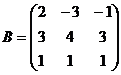
Ответ: а) 1; б) 0; в) 3.
9. Решить систему методом Гаусса:
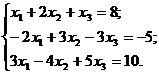
а) 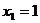 ;
; 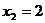 ;
; 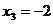 ;
;
б) 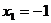 ;
; 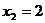 ;
; 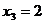 ;
;
в) 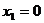 ;
; 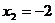 ;
; 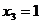 .
.
10. Сформулировать теорему Лапласа и записать формулы разложения по элементам строки 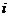 и столбца
и столбца 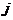
Вариант II
1. Данная запись есть
а) Определитель 3го порядка;
б) Матрица размера 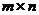 ;
;
в) Единичная матрица.

2. Если 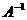 - матрица, транспонированная по отношению к матрице
- матрица, транспонированная по отношению к матрице  , то ее определитель
, то ее определитель
а) Равен 0;
б) Равен 1;
в) Равен 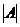 .
.
3. Данная матрица есть
а) Матрица – столбец;
б) Нулевая;
в) Диагональная.
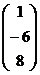
4. Данные формулы позволяют вычислить определитель:
а) 2го порядка;
б) по правилу Сарруса;
в) по теореме Лапласа.
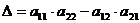
5. Матрицу  можно возвести в степень, если матрица
можно возвести в степень, если матрица 
а) квадратная;
б) размера 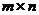 ,
, 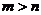 ;
;
в) размера 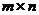 ,
, 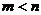 .
.
6. Матрицу  можно умножать на матрицу
можно умножать на матрицу 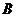 , если:
, если:
г) число столбцов матрицы  больше числа строк матрицы
больше числа строк матрицы 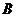 ;
;
д) число столбцов матрицы А меньше числа строк матрицы В;
е) число столбцов матрицы А равно числу строк матрицы В.
7. Перемножить матрицы
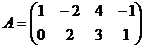 и
и 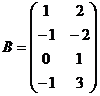
Ответ: а) 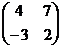 ; б)
; б) 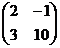 ; в)
; в) 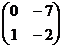 .
.
8. Посчитать определитель по правилу Сарруса:
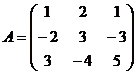
Ответ: а)0; б) 4; в) 12.
9. Решить систему методом Крамера:
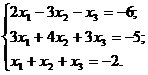
ж) 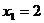 ;
; 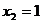 ;
; 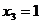 ;
;
з) 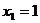 ;
; 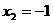 ;
; 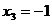 ;
;
и) 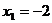 ;
; 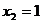 ;
; 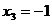 .
.
10. Дать определение матрицы размера 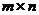 и записать ее в общем виде.
и записать ее в общем виде.
ЛИТЕРАТУРА
1.Высшая математика для экономистов - Учебник для вузов под ред. Н.Ш. Кремер и др., - Москва, ЮНИТИ, 2003.
2.Барковський В.В., Барковська Н.В. - Вища математика для економістів – Київ, ЦУЛ, 2002.
