Общий вид систем линейных неоднородных алгебраических уравнений понятия решения. фундаментальной системы решений. условия совместимости.

Рассмотрим произвольную совместную неоднородную систему линейных алгебраических уравнений:

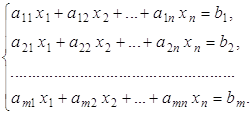
Пусть у нее в общем случае 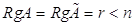, то есть имеется бесконечное множество решений.

Теорема 4.1. Сумма любого решения неоднородной системы линейных алгебраических уравнений с любым решением соответствующей ей однородной системы является решением неоднородной системы.

Доказательство. Возьмем произвольное решение неоднородной системы

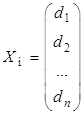и произвольное решение соответствующей ей однородной системы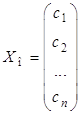

Рассмотрим их сумму .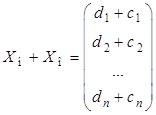

Если данная сумма является решением неоднородной системы, то она должна превратить в тождество любое ее уравнение:

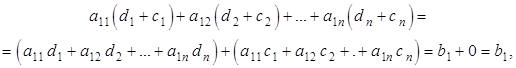
что и требовалось доказать.

Теорема 4.2. Разность любых двух решений неоднородной системы линейных алгебраических уравнений является решением соответствующей однородной системы.

Доказательство. Возьмем два произвольных решения неоднородной системы линейных алгебраических уравнений:

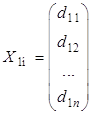и .

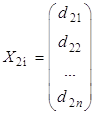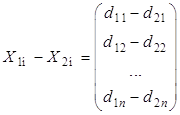
Составим их разность .

Подставим полученную разность в любое уравнение неоднородной системы:

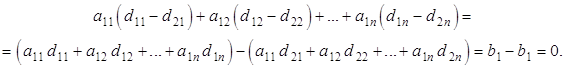
Так как левая часть уравнения обратилась в ноль, значит, 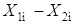является решением однородной системы, что и требовалось доказать.

Из теоремы 4.2 следует, что если 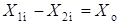, то 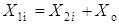. Иначе говоря, взяв какое-то одно решение неоднородной системы линейных алгебраических уравнений 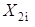и прибавляя к нему разные решения соответствующей однородной системы 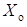, получим разные решения неоднородной системы, что подтверждается теоремой 4.1. Следствие. Общее решение неоднородной системы линейных алгебраических уравнений равно сумме какого-то частного ее решения и общего решения соответствующей однородной системы.

Теорема Кронекера – Капелли.

Пусть дана произвольная система m линейных уравнений с n неизвестными

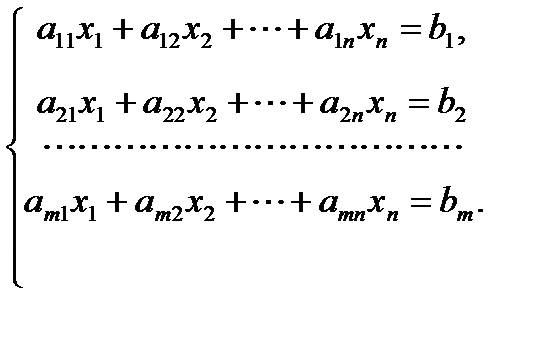
Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера-Капелли.

Примем ее без доказательства.

Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.

11. Система трех линейных неоднородных алгебраических уравнений: определение и метод Крамера решения. Примеры.Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в котором является линейным — алгебраическим уравнением первой степени.
Общий вид системы линейных алгебраических уравнений:

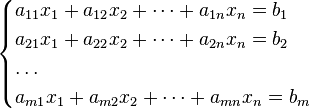Здесь 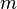— количество уравнений, а 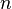— количество переменных, 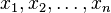— неизвестные, которые надо определить, к оэффициенты 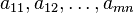и свободные члены 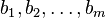предполагаются известными. Индексы коэффициентов в системах линейных уравнений ( 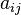) формируются по следующему соглашению: первый индекс ( 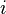) обозначает номер уравнения, второй ( 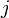) — номер переменной, при которой стоит этот коэффициент[1]. Система называется однородной, если все её свободные члены равны нулю ( 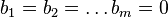), иначе —неоднородной. Ме́тод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы(причём для таких уравнений решение существует и единственно)

Пример.Система линейных уравнений с вещественными коэффициентами: 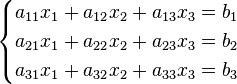Определители: