Знакопеременные ряды. Абсолютная и условная сходимость

В этом параграфе рассматриваются ряды с членами произвольных знаков. Такие ряды называются знакопеременными. Пусть дан знакопеременный ряд:

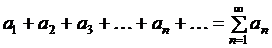. (2.1)

Рассмотрим, наряду с этим, ряд из абсолютных величин членов ряда (2.1):

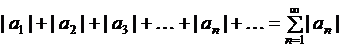. (2.2)

Определение 2.1. Ряд (2.1) с членами произвольных знаков называется абсолютно сходящимся, если сходится ряд (2.2) из модулей членов ряда (2.1).

Теорема 2.1. Абсолютно сходящийся ряд есть ряд сходящийся.

►По условию, ряд (2.1) абсолютно сходящийся. Это означает, что сходится ряд (2.2). Рассмотрим два вспомогательных ряда:

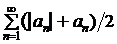, (2.3)

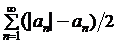.(2.4)

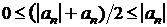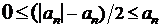Ряды (2.3) и (2.4) – ряды с неотрицательными членами, так как в силу свойств абсолютных величин имеем |a_n| ³ a_nи |a_n| ³ -a_n. С другой стороны, и . Но тогда по признаку сравнения ряды (2.3) и (2.4) сходятся, ибо сходится ряд 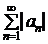, и, следовательно, по свойству 2 рядов (гл. 1, § 3) сходится и ряд . ◄

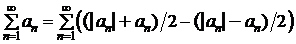Замечание 2.1. Доказанная теорема необратима. Может оказаться, что ряд знакопеременный ряд (2.1) сходится, а ряд (2.2), составленный из модулей членов ряда (2.1), расходится.

Определение 2.2. Если знакопеременный ряд (2.1) сходится, а ряд (2.2), составленный из модулей членов ряда (2.1), расходится, то данный знакопеременный ряд (2.2) называется условно сходящимся.

Определение 2.3.Ряд

u₁ + u₂ + ¼ + u_n + ¼ (2.4)

называется знакочередующимся, если неравенство u_n×u_n+1 < 0 верно для любого n Î N, т. е. если соседние члены ряда имеют различные знаки.

Пусть для определённости u₁>0. Станем обозначать через a_nмодуль n-го члена ряда. Тогда знакочередующийся ряд (2.4) запишется в виде

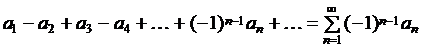. (2.5)

Для знакочередующихся рядов имеется достаточно общий и практически удобный признак сходимости, принадлежащий Лейбницу.

Теорема 2.2(признак Лейбница). Если модули членов знакочередующегося ряда (2.5) монотонно убывают, т.е. a₁ ³ a₂ ³ a₃ ³ ¼ ³ a_n ³ ¼ , а 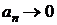при 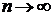, то ряд (2.5) сходится.

Замечание 2.2.Обращаемвнимание читателя на то, что для применения признака Лейбница ряд должен удовлетворять трём условиям:

1) ряд должен быть знакочередующимся;

2) модуль общего член ряда должен стремиться к нулю при n ® ¥.

3) модуль члена ряда должен монотонно убывать с ростом его номера;

Каждое из этих условий необходимо проверить. Нарушение хотя бы одного из них может привести к неверному выводу о сходимости ряда.

Пример 2.1.Доказать что сходится знакочередующийся ряд

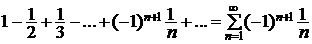. (2.6)

► Поскольку 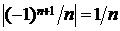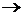0 при 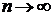, монотонно убывая, то данный ряд сходится по признаку Лейбница. ◄

Так, знакочередующийся ряд 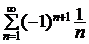сходится (пример 1.1), а ряд 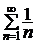, составленный из модулей его членов, расходится. Следовательно, ряд 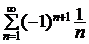сходится условно.

Все сходящиеся ряды можно разделить на два класса: абсолютно сходящиеся ряды и условно сходящиеся ряды. Отметим, что все сходящиеся ряды с неотрицательными членами входят в класс абсолютно сходящихся рядов.

Для установления абсолютной сходимости знакопеременного ряда к ряду из модулей членов этого ряда можно применить признаки сходимости, установленные для рядов с неотрицательными членами. Но нужно помнить, что из расходимости ряда 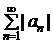не всегда следует расходимость ряда 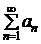. Ряд 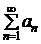может сходиться условно.

Замечание 2.3. Пусть с помощью признака Даламбера установлено, что знакопеременный ряд абсолютно не сходится, тогда модули его членов монотонно возрастают (замечание 4.2, гл. 2). Итак, в этом случае общий член знакопеременного ряда не может стремиться к нулю с возрастанием номера.

Абсолютно сходящиеся ряды обладают целым рядом свойств, присущих конечным суммам.