Абсолютная и условная сходимость рядов

Рассмотрим произвольный знакопеременный числовой ряд (1) 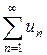. Составим из абсолютных величин его членов ряд

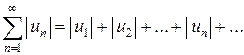. (4)

Теорема 10. Если ряд (4) сходится, то ряд (1) также сходится.

Определение. Числовой ряд (1) называется абсолютно сходящимся, если сходится ряд (4), составленный из модулей его членов.

Определение. Числовой ряд (1) называется условно сходящимся, если сам он сходится, а ряд (4), составленный из модулей его членов, расходится.

Пример 11. Ряд 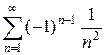сходится абсолютно, так как ряд 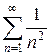, составленный из модулей его членов, сходится (будучи обобщённым гармоническим рядом с показателем ).

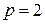Пример 12. В примере 9 показано, что ряд 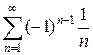сходится согласно признаку Лейбница. Однако ряд из абсолютных величин его членов есть расходящийся гармонический ряд 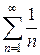, поэтому ряд 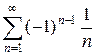сходится лишь условно.

Для произвольного ряда задача «исследовать сходимость» означает установление факта сходимости или расходимости этого ряда и, в случае сходимости, проверку того, как сходится этот ряд: абсолютно или условно.

Во многих случаях об абсолютной сходимости того или иного ряда можно судить на основании уже известных признаков (теоремы 5 – 7), соответствующим образом переформулированных.

Признак сравнения: если члены ряда (u) 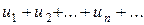, взятые по модулю, не превосходят соответствующих членов сходящегося ряда (v) 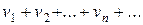с положительными членами: 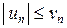, , 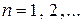то ряд (u) сходится, притом абсолютно.

Замечание. Если 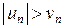и ряд (v) расходится, то ряд (u) не обязательно расходится! Он может и сходиться условно! Таким образом, часть б) теоремы 5, касающаяся расходимости ряда с бóльшими членами, здесь не работает.

Признак Даламбера: если для ряда 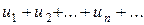существует конечный предел 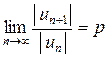, то при 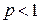данный ряд сходится, притом абсолютно, при 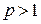– расходится.

Радикальный признак Коши:если для ряда 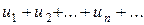существует конечный предел 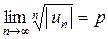, то при 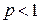данный ряд сходится, притом абсолютно, при 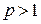– расходится.

Замечание. Расходимость при 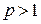следует из того, что тогда .

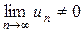Необходимость различать абсолютно и условно сходящиеся ряды объясняется их существенно различными свойствами и, прежде всего, следующим:

Теорема 11 (переместительное свойство абсолютно сходящегося ряда). Если в абсолютно сходящемся ряде переставить как угодно члены, то получится абсолютно сходящийся ряд, сумма которого равна сумме исходного.

Условно сходящиеся ряды переместительным свойством «от перемены мест слагаемых сумма не меняется» не обладают. В любом условно сходящемся ряде можно так переставить члены, чтобы вновь полученный ряд имел наперёд заданную сумму. Более того, можно так переставить члены условно сходящегося ряда, что он станет расходящимся.

Функциональные ряды

Определение. Ряд называется функциональным, если его члены являются функциями одной действительной переменной :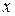

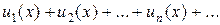. (1)

Если подставить в (1) вместо 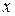числовое значение 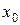из области определения функций 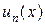, то получится числовой ряд

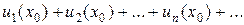, (2)

который может оказаться сходящимся или расходящимся.

Определение. Если числовой ряд (2) сходится, то значение 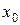называется точкой сходимости функционального ряда (1).

Определение. Множество всех точек сходимости функционального ряда (1) называется его областью сходимости.

Определение. Функциональный ряд (1) называется абсолютно сходящимся в точке 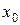, если соответствующий числовой ряд (2) абсолютно сходится. Если ряд (1) сходится абсолютно в каждой точке некоторого множества 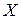, то его называют абсолютно сходящимся на множестве .

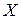Пример 1. Функциональный ряд 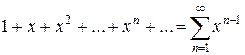является геометрическим рядом со знаменателем 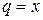, поэтому сходится при 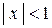, т.е. имеет областью сходимости интервал 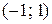. При этом ряд абсолютно сходится на всей области сходимости, так как ряд из модулей 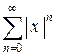сходится при .

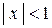Обозначим через 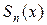сумму первых n членов функционального ряда (1). Из определения точки сходимости следует, что для каждой точки сходимости 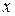существует предел 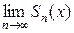, равный некоторому числу 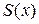. Тем самым на области сходимости определена однозначная функция 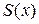, называемая суммой функционального ряда (1). Как и для числовых рядов, пишут тогда

.

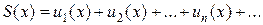Так, ряд из примера 1 при 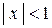имеет сумму .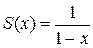