Глава 2. Cходимость числовых рядов

С неотрицательными членами

Признаки сравнения для рядов с неотрицательными членами

Признаки сравнения позволяют свести решение вопроса о сходимости данного ряда к вопросу о сходимости другого более простого ряда или ряда, поведение которого уже выяснено.

Теорема 2.1 (признак сравнения в форме неравенства). Пусть имеются два ряда с неотрицательными членами

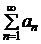, (2.1) 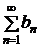, (2.2)

причём члены ряда (2.1) не превосходят соответствующих членов ряда (2.2):

0 £ a_n £ b_n, 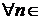N. (2.3)

Тогда из сходимости ряда (2.2) следует сходимость ряда (2.1), а из расходимости (2.1) ряда следует расходимость ряда (2.2).

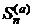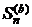►Обозначим через и частичные суммы этих рядов. Из неравенства (2.3) следует, что

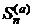
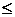
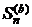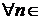, N. (2.4)

Пусть ряд (2.2) сходится. Тогда последовательность 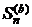ограничена, поэтому в силу (2.4) ограничена и последовательность 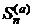. Отсюда заключаем, в силу упомянутой теоремы, что сходится и ряд (2.1).

Пусть ряд (2.1) расходится. Надо доказать, что ряд (2.2) также расходится. Предположим противное: этот ряд сходится. Тогда из вышепоказанного следует, что ряд (2.1) сходится. Полученное противоречие с условием расходимости этого ряда доказывает вторую часть теоремы. ◄

Пример 2.1.Доказать, что 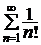сходится.

►Имеем: 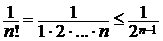, 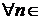N. Ряд 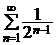сходится, ибо это геометрический ряд 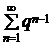при 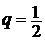(пример 1.1, гл. 1). Тогда в силу теоремы 2.1 сходится и данный ряд.

Замечание 2.1. Теорема 2.1 остаётся справедливой, если неравенство (2.1) выполняется не для любого натурального n, а начиная с некоторого m >1 (следствие 1 из теоремы 3.1 гл. 1).

Теорема 2.2 (признак сравнения в предельной форме). Пусть члены рядов

(2.1) и (2.2) строго положительны, т.е. a_n > 0, b_n > 0 для всех n Î N. Если

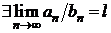, l ¹ 0, l ¹ +¥,

то данные ряды сходятся или расходятся одновременно.

Замечание 2.1. Если 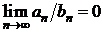, то можно лишь утверждать, что из сходимости ряда 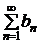следует сходимость ряда .

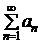Замечание 2.2. Для применения признаков сравнения надо иметь арсенал «эталонных рядов», как сходящихся, так и расходящихся, с которыми сравниваются исследуемые ряды. Одним из них является так называемый обобщённый гармонический ряд 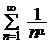. В § 3 будет показано, что он сходится при a > 1 и расходится при a £ 1. Другим «эталонным» рядом является геометрический ряд 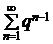, сходящийся при |q| < 1 и расходящийся при |q| ³ 1 (пример 1.1).

Следствие 2.1 из теоремы 2.2.Пусть дан ряд 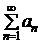с положительными членами, причём 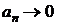при 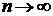. Если 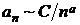при n ® ¥, где С – постоянное число, тогда рассматриваемый ряд сходится при a > 1 и расходится при 0 ≤ a £ 1 (здесь ~ является знаком эквивалентности).

Пример 2.3.Исследовать на сходимость ряд .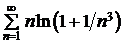

►Имеем: 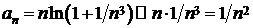при n ® ¥. В этом случае a = 2 > 1, следовательно, данный ряд сходится (следствие 2.1).◄

Интегральный признак Коши

Теорема 3.1 (интегральный признак Коши). Пусть функция f(x) непрерывна, положительна и убывает при x ³ 1. Тогда ряд 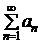, где a_n = f(n) для nÎN, и несобственный интеграл 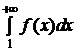либо оба сходятся, либо оба расходятся.

Пример 3.1.Исследовать на сходимость обобщённый гармонический ряд 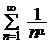в зависимости от значения параметра a.

► Заметим, что при a £ 0 общий член ряда не стремится к нулю с увеличением номера, следовательно, не выполняется необходимое условие сходимости ряда, поэтому в этом случае обобщённый гармонический ряд расходится.

При a = 1 получаем гармонический ряд, он расходится.

В случае a > 0, a ≠ 1 рассмотрим функцию 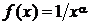. Легко проверить, что она удовлетворяет при x ³ 1 всем условиям теоремы 3.1. Исследуем на сходимость несобственный интеграл 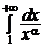при данных значениях a .

1. 0 < a < 1Þ 1 - a > 0 Þ 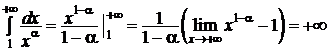– несобственный интеграл расходится и, следовательно, рассматриваемый ряд расходится при 0 < a < 1.

2. a > 1 Þ 1 - a < 0 Þ 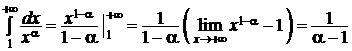, поэтому несобственный интеграл сходится, а вместе с ним сходится и обобщённый гармонический ряд при указанных значениях a.

Итак, ряд 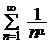расходится при a £ 1 и сходится при a > 1. ◄

Пример 3.2.Исследовать сходимость ряда .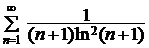

►Пусть 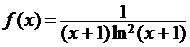. Легко проверить, что функция f(x) удовлетворяет всем условиям теоремы 3.1. Но интеграл

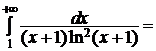
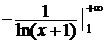
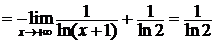сходится.

Следовательно, сходится и данный ряд.◄