Основные свойства сходящихся рядов

Основные свойства сходящихся рядов

Свойство 1.Пусть ряд

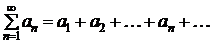(3.1)

сходится, S − его сумма, а c – некоторое вещественное число. Тогда ряд

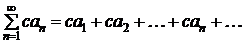(3.2)

тоже сходится, и его сумма равна cS.

Свойство 2. Если ряды 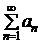и 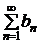сходятся, а A и B – их суммы, то ряд 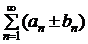, называемый суммой (разностью) данных рядов, тоже сходится, и его сумма равна A ± B.

Замечание 3.1. Раскрывать скобки в сходящемся ряде, вообще говоря, нельзя. Например, ряд (1 - 1) + (1 - 1) + ¼ + (1 - 1) + ¼ сходится, и его сумма S = 0; если же раскрыть скобки, то получится расходящийся ряд: 1 - 1 + 1 - 1 + ¼ .

Докажем, например, свойство 1.

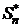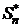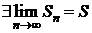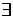
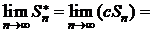
►Пусть S_nи − n-е частичные суммы рядов (3.1) и (3.2) соответственно. Имеем: = ca₁ + ¼ + ca_n = c(a₁ + ¼ + a_n) = cS_n. По условию ряд (3.1) сходится к сумме S, поэтому . Но тогда 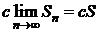Þ Þ ряд (3.2) сходится, его сумма равна cS.◄

Замечание 3.2. Если ряд 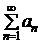сходится, а ряд 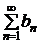расходится, то сумма этих рядов есть ряд расходящийся. Действительно, если предположить сходимость ряда 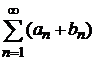, то по свойству 2 сходящихся рядов будет сходиться ряд 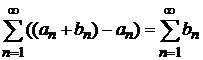, а по условию он расходится;

Замечание 3.3. Из расходимости рядов 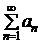и 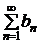расходимость ряда 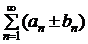не следует. Так, если 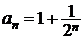, , 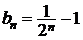ряды 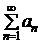и 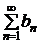расходятся, а ряд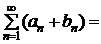 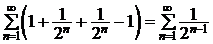сходится. Однако, если 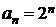, , 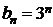то ряд 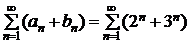будет расходиться.

Определение 3.1. Пусть дан ряд (3.1) и любое натуральное число m. Ряд

a_m+1 + a_m+2 + ¼ + a_m+k ¼= 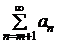(3.3)

называется остатком ряда (3.1) после m-го члена.

Теорема 3.1. Ряд (3.1) и его остаток (3.3) после m-го члена сходятся или расходятся одновременно.

►Обозначим n-ю частичную сумму ряда (3.1) через 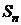, а k-ю частичную сумму ряда (3.3) – через 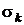. При 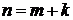имеем:

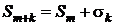. (3.4)

Здесь S_m − некоторое число, так как m фиксировано.

Пусть ряд (3.1) сходится, и его сумма равна S. Из этого следует, что существует конечный 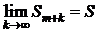. Но тогда из (3.4) следует, что существует конечный 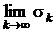, причём 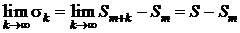. Последнее означает, что ряд (3.3) сходится и его сумма s равна S − S_m. Итак, из сходимости ряда (3.1) следует сходимость ряда (3.3).

Пусть теперь ряд (3.3) сходится и его сумма равна s. Это означает, что существует конечный 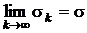. Переходя в (3.4) к пределу при k ® ¥ получаем

,

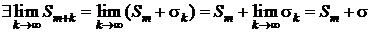следовательно, ряд (3.1) сходится, и его сумма S равна 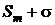. Итак, из сходимости ряда (3.3) следует сходимость ряда (3.1).

Вторая часть теоремы доказывается от противного. Пусть один из рядов (3.1), (3.3) расходится. Требуется доказать, что тогда расходится и другой ряд. Допустим, что он сходится. Но тогда, по доказанному выше должен сходиться и первый ряд, что противоречит условию. Значит, ряды (3.1) и (3.3) расходятся одновременно.◄

Следствие 1 из теоремы 3.1.Отбрасывание любого числа первых членов ряда не влияет на его сходимость.

Следствие 2 из теоремы 3.1.Для того, чтобы сходился ряд (3.1) необходимо и достаточно чтобы его остаток после n-го члена стремился к нулю при .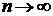

Глава 2. Cходимость числовых рядов

С неотрицательными членами

Интегральный признак Коши

Теорема 3.1 (интегральный признак Коши). Пусть функция f(x) непрерывна, положительна и убывает при x ³ 1. Тогда ряд 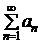, где a_n = f(n) для nÎN, и несобственный интеграл 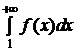либо оба сходятся, либо оба расходятся.

Пример 3.1.Исследовать на сходимость обобщённый гармонический ряд 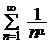в зависимости от значения параметра a.

► Заметим, что при a £ 0 общий член ряда не стремится к нулю с увеличением номера, следовательно, не выполняется необходимое условие сходимости ряда, поэтому в этом случае обобщённый гармонический ряд расходится.

При a = 1 получаем гармонический ряд, он расходится.

В случае a > 0, a ≠ 1 рассмотрим функцию 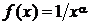. Легко проверить, что она удовлетворяет при x ³ 1 всем условиям теоремы 3.1. Исследуем на сходимость несобственный интеграл 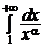при данных значениях a .

1. 0 < a < 1Þ 1 - a > 0 Þ 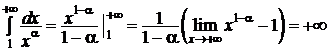– несобственный интеграл расходится и, следовательно, рассматриваемый ряд расходится при 0 < a < 1.

2. a > 1 Þ 1 - a < 0 Þ 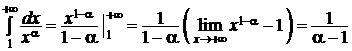, поэтому несобственный интеграл сходится, а вместе с ним сходится и обобщённый гармонический ряд при указанных значениях a.

Итак, ряд 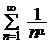расходится при a £ 1 и сходится при a > 1. ◄

Пример 3.2.Исследовать сходимость ряда .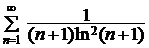

►Пусть 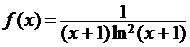. Легко проверить, что функция f(x) удовлетворяет всем условиям теоремы 3.1. Но интеграл

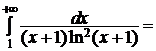
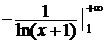
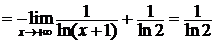сходится.

Следовательно, сходится и данный ряд.◄

В ряды Маклорена

Пусть функция f(x) имеет производные любого порядка в некоторой окрестности точки 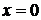. В равенстве (3.3) положим a = 0, ряд (3.3) принимает вид:

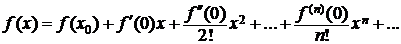
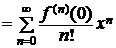. (4.1)

Ряд (4.1) называют рядом Маклорена. Ряд Маклорена − это ряд по степеням х.

Напишем для f(x) формулу Маклорена с остаточным членом в форме Лагранжа:

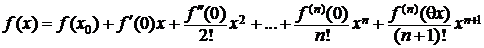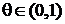, . (4.2)

Используя равенство (4.2) и теорему 3.2, разложим в ряд Маклорена функции: e^x , sin x, cos x, ln(1 + x), acrtg x, (1+ x)^α. Предварительно докажем лемму.

Лемма. 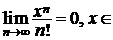R.

►Рассмотрим ряд 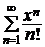и исследуем его на абсолютную сходимость по признаку Даламбера. Имеем:

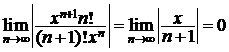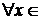при R.

Данный ряд сходится абсолютно на всей вещественной оси, поэтому его общий член стремится к нулю 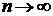при при 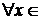R, т.е. .◄

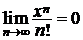1. 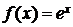, 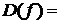R. Имеем f ⁽ⁿ⁾(x) = e^x, f ⁽ⁿ⁾(0) = 1, f⁽ⁿ⁺¹⁾(θх) = e^θх для 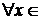R и 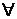nÎN. Напишем для f(x) = e^xформулу Маклорена вида (4.2):

, .

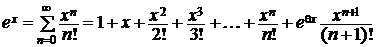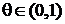Для остаточного члена R_n(x) 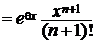справедливо неравенство:

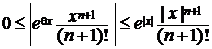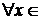для R.

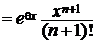
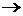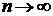Отсюда следует с учётом леммы, что R_n(x) 0 при для 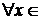R. Но тогда ряд Маклорена

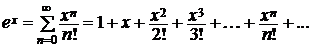(4.3)

в силу теоремы 4.2 сходится к функции e^xвсей вещественной оси.

2. f(x) = sinx, 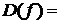R. Имеем f ⁽ⁿ⁾(x) = ,

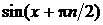f ⁽ⁿ⁾(0) =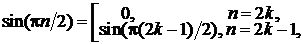

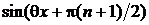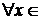f ⁽ⁿ⁺¹⁾(θх) = для R и 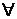n Î N,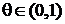

Имеем 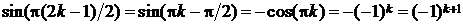, 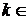Z. Отсюда для производных от функции f(x) = sinx в точке х = 0 имеем равенство:

f ^(2k)(0)=0, f ^(2k−1)(0)=(−1)^k+1.

Напишем для f(x) = sinx формулу Маклорена вида (6.2):

, .

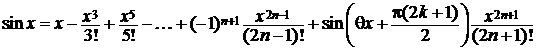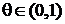Для остаточного члена R_n(x) 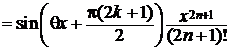верно неравенство:

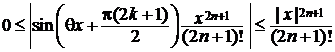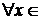для R.

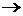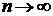Отсюда, с учётом леммы, следует, что R_n(x) 0 при для 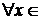R. Но тогда ряд Маклорена

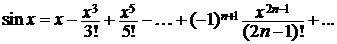(4.4)

в силу теоремы 4.2 сходится к функции sinx на всей вещественной оси.

3.f(x) = cosx, 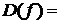R. Ряд Маклорена можно получить, рассуждая так же, как в случае функции sinx. Однако рациональнее применить теорему о почленном дифференцировании степенного ряда. Запишем ряд (6.4) в несколько ином виде:

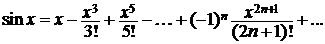
и продифференцируем обе части полученного равенства:

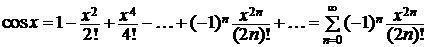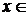, R. (4.5)

Основные свойства сходящихся рядов

Свойство 1.Пусть ряд

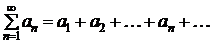(3.1)

сходится, S − его сумма, а c – некоторое вещественное число. Тогда ряд

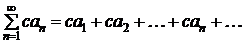(3.2)

тоже сходится, и его сумма равна cS.

Свойство 2. Если ряды 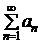и 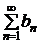сходятся, а A и B – их суммы, то ряд 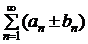, называемый суммой (разностью) данных рядов, тоже сходится, и его сумма равна A ± B.

Замечание 3.1. Раскрывать скобки в сходящемся ряде, вообще говоря, нельзя. Например, ряд (1 - 1) + (1 - 1) + ¼ + (1 - 1) + ¼ сходится, и его сумма S = 0; если же раскрыть скобки, то получится расходящийся ряд: 1 - 1 + 1 - 1 + ¼ .

Докажем, например, свойство 1.

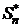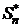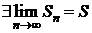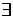
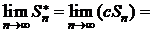
►Пусть S_nи − n-е частичные суммы рядов (3.1) и (3.2) соответственно. Имеем: = ca₁ + ¼ + ca_n = c(a₁ + ¼ + a_n) = cS_n. По условию ряд (3.1) сходится к сумме S, поэтому . Но тогда 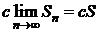Þ Þ ряд (3.2) сходится, его сумма равна cS.◄

Замечание 3.2. Если ряд 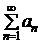сходится, а ряд 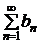расходится, то сумма этих рядов есть ряд расходящийся. Действительно, если предположить сходимость ряда 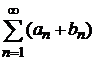, то по свойству 2 сходящихся рядов будет сходиться ряд 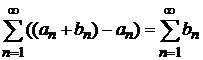, а по условию он расходится;

Замечание 3.3. Из расходимости рядов 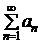и 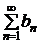расходимость ряда 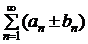не следует. Так, если 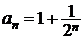, , 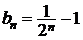ряды 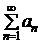и 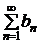расходятся, а ряд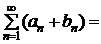 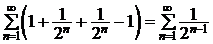сходится. Однако, если 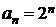, , 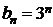то ряд 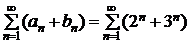будет расходиться.

Определение 3.1. Пусть дан ряд (3.1) и любое натуральное число m. Ряд

a_m+1 + a_m+2 + ¼ + a_m+k ¼= 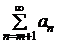(3.3)

называется остатком ряда (3.1) после m-го члена.

Теорема 3.1. Ряд (3.1) и его остаток (3.3) после m-го члена сходятся или расходятся одновременно.

►Обозначим n-ю частичную сумму ряда (3.1) через 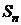, а k-ю частичную сумму ряда (3.3) – через 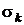. При 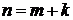имеем:

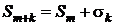. (3.4)

Здесь S_m − некоторое число, так как m фиксировано.

Пусть ряд (3.1) сходится, и его сумма равна S. Из этого следует, что существует конечный 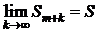. Но тогда из (3.4) следует, что существует конечный 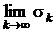, причём 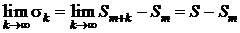. Последнее означает, что ряд (3.3) сходится и его сумма s равна S − S_m. Итак, из сходимости ряда (3.1) следует сходимость ряда (3.3).

Пусть теперь ряд (3.3) сходится и его сумма равна s. Это означает, что существует конечный 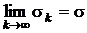. Переходя в (3.4) к пределу при k ® ¥ получаем

,

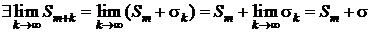следовательно, ряд (3.1) сходится, и его сумма S равна 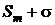. Итак, из сходимости ряда (3.3) следует сходимость ряда (3.1).

Вторая часть теоремы доказывается от противного. Пусть один из рядов (3.1), (3.3) расходится. Требуется доказать, что тогда расходится и другой ряд. Допустим, что он сходится. Но тогда, по доказанному выше должен сходиться и первый ряд, что противоречит условию. Значит, ряды (3.1) и (3.3) расходятся одновременно.◄

Следствие 1 из теоремы 3.1.Отбрасывание любого числа первых членов ряда не влияет на его сходимость.

Следствие 2 из теоремы 3.1.Для того, чтобы сходился ряд (3.1) необходимо и достаточно чтобы его остаток после n-го члена стремился к нулю при 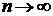.