Если ряд, составленный из абсолютных членов данного ряда, сходится, то сходится и данный ряд.

S_n – частичная сумма ряда (*). σ _n - частичная сумма ряда (**).

S_n′ − сумма всех положительных членов ряда (*), входящих в S_n; S_n′′ − сумма абсолютных величин всех отрицательных членов, входящих в S_n.

S_n = S_n′ − S_n ′′; σ_n = S_n′ + S_n′′, S _n′ ≤ σ _n < σ, где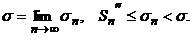

S _n′ и S_n′′ монотонно возрастают с возрастанием n и остаются ограниченными сверху. Следовательно,

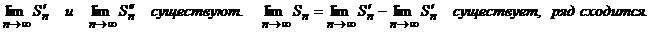
Этот признак является достаточным, но не является необходимым. Существуют такие ряды, которые сами сходятся, но ряды, составленные из абсолютных величин, расходятся.

Например, 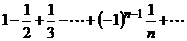сходится,

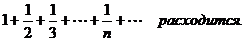
Если ряд (**) сходится, то ряд (*) называетсяабсолютно сходящимся.

Если ряд (*) сходится, а ряд (**) расходится, то ряд (*) называется условно сходящимся.

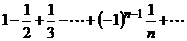− условно сходится.

П р и м е р .

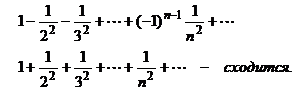
Исходный ряд сходится абсолютно.

Функциональные ряды.

Рассмотрим ряд

u₁(x) + u₂(x) + … + u_n(x) + … (1)

Ряд (1) – функциональный ряд.

Введем понятие сходимости ряда (1). Зафиксируем значение x. Тогда

u₁(x) + u₂(x) + … + u_n(x) = S_n(x) – частичная сумма ряда. 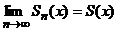- сумма ряда.

Таким образом, суммой S(x) функционального ряда является функция от x.

Если числовой ряд (2) сходится, то ряд (1) называется сходящимся в точке x .

Множество точек числовой оси, в которых ряд (1) сходится, называется областью сходимости функционального ряда.

Суммой S(x) функционального ряда является функция от x.

П р и м е р . 1 + x + x² + … + xⁿ + … − геометрическая прогрессия со знаменателем q = x. Ряд сходится, если |x| < 1, сумма ряда S(x) = ¹/ _{(1 – x)}.

Сходимость ряда к функции S(x) означает следующее. При фиксированном x каково бы ни было ε > 0 найдется такой номер N, что для всех n > N выполняется неравенство

|S_n(x) – S(x)| < ε. (*)

Номер N, начиная с которого выполняется неравенство (*), зависит от выбора ε и , вообще говоря, зависит от x. т.е. N может разным при различных x.

Ряд (1) называется равномерно сходящимся к функции S(x)) каково бы ни было ε, найдется такой независящий от x номер N, что для любого n ≥ N выполняется неравенство (*)

|S_n(x) – S(x)| < ε.

Замечание.

y ε

y = S(x)

ε

x

A b

Полученный результат можно геометрически интерпретировать следующим образом. Рассмотрим график функции y = S(x). Построим около этой кривой полосу шириной 2ε, т.е. построим кривые y = S(x) + ε иy = S(x) – ε. Тогда при любом ε график функции s_n(x), будет лежать целиком в рассматриваемой полосе. В этой же полосе и будут лежать графики всех последующих частичных сумм.

Определение.

Функциональный ряд (1) называетсямажорируемымв некоторой области изменения х, если существует такой сходящийся числовой ряд

α₁ + α₂ + …+ α_n + … (2)

с положительными членами, что для всех х из данной области выполняются соотношения

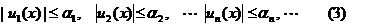
Пример.

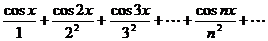
Ряд является мажорируемым на всей числовой оси. Действительно, для всех х выполняется условие

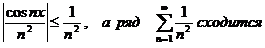
Всякий мажорируемый ряд является абсолютно сходящимся

Можно показать, что всякий мажорироемый ряд является равномерно сходящимся

Свойства равномерно сходящихся рядов.

Непрерывность суммы ряда.

Сумма равномерно сходящегося ряда непрерывных функций есть функция непрерывная.

2. Равномерно сходящиеся ряды можно почленно интегрировать т.е.

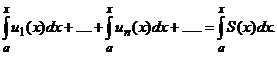
3. Равномерно сходящиеся ряды можно почленно дифференцировать т.е.

u₁′(x) + u₂′(x) + ....+ u_n′(x) +.... =S ′(x)

Степенные ряды.