Знакочередующиеся ряды. Признак Лейбница.

Определение. Ряд называется знакочередующимся, если каждые два соседние его слагаемые имеют разный знак: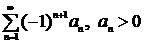

Сформируем достаточный признак сходимости такого ряда.

ТЕОРЕМА 1 (признак Лейбница). Пусть ряд 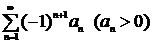знакочередующийся, последовательность 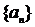монотонно убывает и 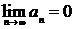. Тогда ряд (1) сходится, его сумма .

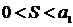Следствие. 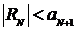, то есть погрешность приближённого вычисления знакочередующегося ряда по частичной сумме не превосходит абсолютной величины первого отброшенного члена.

Пример 1. Сколько слагаемых нужно взять, чтобы вычислить 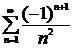с точностью до 0,001?

Решение. Можно записать два неравенства:

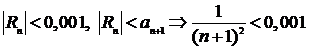
Найдём 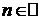: 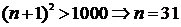. Ответ: 31 слагаемое.

Ряды с произвольным членами, абсолютная и условная сходимости.

Определение. Ряд называется знакопеременным, если его общий член может быть как положительным, так и отрицательным.

Определение. Ряд 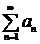сходится абсолютно, если сходится ряд .

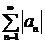Определение. Сходящийся ряд, который не сходится абсолютно, называется условно сходящимся.

ТЕОРЕМА 2. Из сходимости ряда 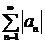следует сходимость ряда .

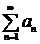Абсолютная сходимость 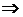сходимость, сходимость 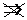абсолютная сходимость.

Замечание. Каждый из рассмотренных нами признаков сходимости знакоположительных рядов может рассматриваться как достоверный признак абсолютной сходимости.

Члены абсолютно сходящегося ряда можно менять местами произвольным образом. Для условно сходящегося — это неверно.

ТЕОРЕМА 3 (Дирихле). Пусть ряд 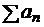сходится абсолютно и его сумма равна 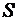. Тогда ряд 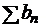, полученный из 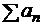произвольной перестановкой его членов также сходится абсолютно, причём к той же сумме 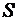(без доказательства).

ТЕОРЕМА 4 (Римана). Пусть ряд 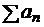сходится условно, 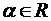. Тогда члены ряда можно переставить так, что его сумма будет равна .

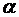Функциональные ряды.

Определение. Пусть 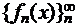— функции, заданные на 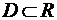. Тогда ряд . 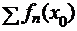называется функциональным рядом.

Определение.Ряд называется 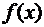сходящимся на множестве 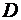, если в каждой точке 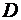ряд сходится как числовой.

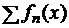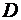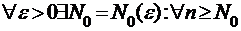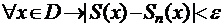Определение. Функциональный ряд равномерно сходится на множестве , если и . Здесь , .

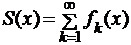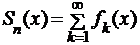Пример 1. Геометрический ряд 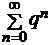— сходится, если 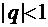, расходится при 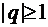. Рассмотрим функциональный ряд: 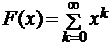. Этот ряд сходится, если 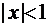(расходится при 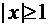) и его сумма 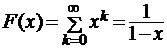при .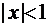

Определение: Функциональный ряд 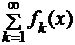мажорируется на множестве 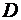сходящимся числовым рядом 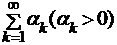, если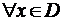

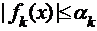
ТЕОРЕМА 1 ((Достаточный) признак Вейерштрасса равномерной сходимости функционального ряда). Пусть ряд 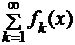(1) мажорируется на 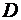сходящимся числовым рядом 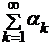(2). Тогда ряд равномерно сходится на .

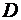Примеры 2-3: Функциональные ряды 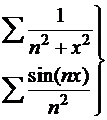равномерно сходятся на 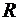, так как они мажорируются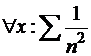

Степенные ряды.

Определение. Функциональный ряд вида 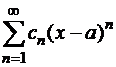(1) называется степенным. Здесь 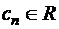— коэффициенты, 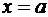— центр степенного ряда. Определение: множество 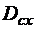точек числовой оси, где сходится ряд (1), называются его областью сходимости.

ТЕОРЕМА 1 (Абеля): 1) Если степенной ряд (1) сходится в точке 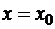, то он сходится, причём абсолютно, .

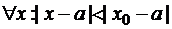2) Если ряд расходится в точке 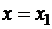, то он расходится, .

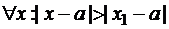Область сходимости степенного ряда всегда - промежуток с центром в точке , причём этот промежуток может являться интервалом или полуинтервалом или отрезком.

Определение: радиусом сходимости степенного ряда (1) называется число 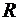: при 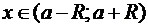ряд сходится, а вне этого интервала — расходится. Если 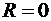, то интервал вырождается в точку 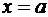(в своём центре сходится любой степенной ряд!); 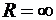— интервал сходимости представляет собой всю числовую ось. Сформулируем результаты, позволяющие вычислить радиус сходимости степенного ряда.

ТЕОРЕМА 2 (Коши-Адамар): Пусть существует .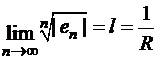

Тогда ряд сходится при 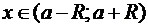и расходится вне этого интервала. Если 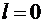, то 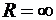, если 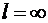, то .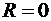

ТЕОРЕМА 3 (Даламбера). Пусть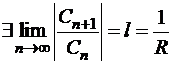

Тогда степенной ряд (1) сходится внутри интервала 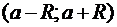и расходится вне его.

Замечания:

1)При 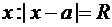, то есть на концах интервала, теоремы 2 и 3 ответа на вопрос о сходимости не дают. В этих точках требуется отдельное исследование.

2)В каждой из этих точек, как показывают примеры ниже, ряд может как сходиться, так и расходиться.

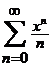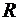Пример 1: степенной ряд: . Его сходимост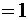и , при 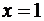ряд расходится как гармонический; 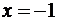, сходится как ряд Лейбница. Таким образом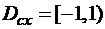

Определение: интервалом сходимости принято называть .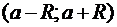

ТЕОРЕМА 4: Пусть степенной ряд (1) сходится на интервале 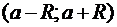. Тогда 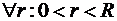ряд равномерно сходится на отрезке .

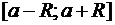СВОЙСТВА СТЕПЕННЫХ РЯДОВ.

Следствие 1: Сумма степенного ряда является непрерывной функцией на всём интервале его сходимости.

Замечание: на отрезке 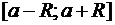сумма степенного ряда может быть разрывной.

Пример 3: геометрический ряд 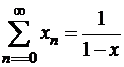сходится на интервале 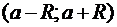и его сумма 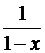непрерывна на этом интервал, но имеет разрыв на правом конце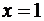

Следствие 2: степенной ряд (1) можно почленно дифференцировать в интервале сходимости; при этом ряд, составленный из производных:

1)также является степенным;

2)имеет тот же радиус сходимости;

3)имеет сумму равную производной суммы исходного ряда (в каждой точке интервала сходимости). (без доказательства)

Следствие 3: степенной ряд можно почленно интегрировать на отрезке 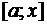с 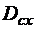; полученный ряд имеет вид 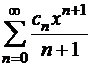и имеет тот же радиус сходимости.

1. Формула Тейлора.

Определение. Пусть 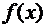дифференцируема до порядка 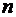включительно в некоторой окрестности точки 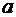. Тогдамногочлен Тейлора 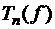или 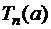определяется по формуле 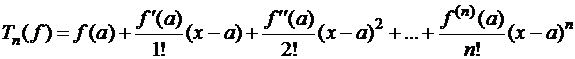(1)

изависит от функции 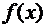, , 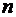точки .

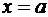Определение.Величину 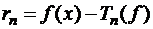(2) назовём остаточным членом формулы Тейлора (остатком).

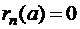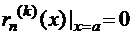Свойства остаточного члена: 1) . 2) , при .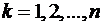

3)Пусть 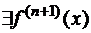в окрестности точки 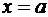. Тогда .

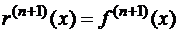ТЕОРЕМА 1 (Формула Тейлора с остаточным членом в форме Пеано).

Пусть функция 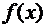имеет в точке 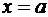все производные до порядка 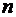включительно.

Тогда в некоторой окрестности точки 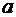имеет место представление:

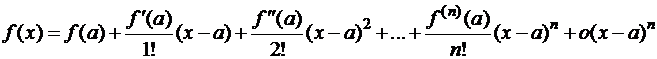Доказательство:Вычислим, последовательно применяя правило Лопиталя:

.

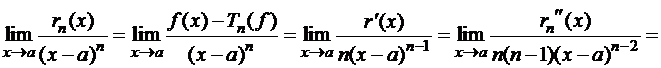
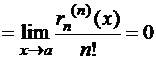ТЕОРЕМА 2 (Формула Тейлора с остаточным членом в форме Лагранжа):

Пусть функция 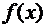имеет все производные до порядка 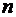включительно на конечном отрезке 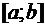. Тогда :

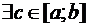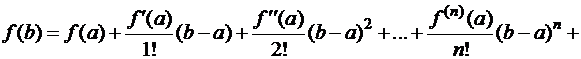
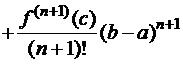. (3)

Ряды Тейлора и Маклорена.

Пусть степенной ряд 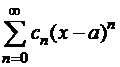(4)имеет радиус сходимости 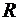. Тогда на 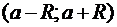ряд (4) сходится к 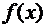(сумме ряда). 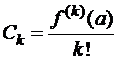(6)

Определение: Ряд (4), где коэффициенты определяются по формуле (6) называются рядом Тейлора функции 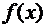в определённой точке .

.

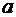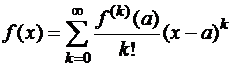Определение: При 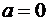ряд Тейлора называется рядом Маклорена.

Степенной ряд (4) является рядом Тейлора для своей суммы 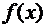на интервале сходимости.

Определение: функция 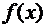называется разложимой в ряд Тейлора в окрестности точки 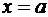, если её ряд Тейлора сходится к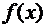 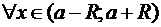, где 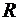— радиус сходимости ряда Тейлора.

ТЕОРЕМА 3: (Необходимое и достаточное условие). Функция 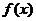разложима в ряд Тейлора на множестве 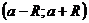если и только если 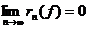для всех .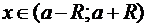