Теорема о равенстве смешанных производных

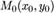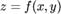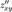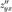Если в некоторой окрестности точки функция имеет смешанные частные производные и , причём эти смешанные частные производные непрерывны в точке м0 , то они равны в этой точке: .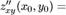

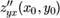Производная по направлению ФМГ

производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Рассмотрим функцию от n аргументов в окрестности точки 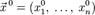. Для любого единичного вектора 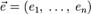определим производную функции f в точке 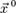по направлению 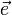следующим образом: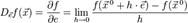

Геометрический смысл дифференциала функции двух переменных

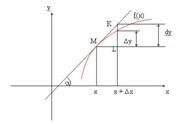
Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx

Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Частные производные высших порядков

Формула Тейлора

Пусть функция f(x,y) имеет полные производные вплоть до n-го порядка включительно в некоторой окрестности точки (x0,y0). Введём дифференциальный оператор

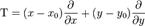
Тогда разложением в ряд Тейлора функции f(x,y) по степеням (x − x0)k и (y − y0)k в окрестности точки (x0,y0) будет

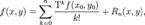
где Rn(x,y) — остаточный член в форме Лагранжа:

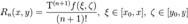
В случае функции одной переменной 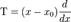, поскольку для функции одной переменной частная производная тождественно равна полной. Аналогично формула распространяется на функции от любого числа переменных, меняется только число слагаемых в операторе T.

Неявная ФМП

при выполнении соответствующих условий, уравнение 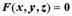задает неявно функцию 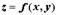. Это же уравнение может задавать неявно функцию 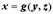или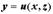

Экстремум ФМП

Пусть функция f (х, у) определена в точке M0 (x0, y0) и в некоторой её окрестности. Функция f (х, у) имеет максимум в точке(x0, y0), если f (x0, y0) > f (х, у) для всех точек (х, у). из некоторой окрестности точки(x0, y0). Если же f (x0, y0) < f (х, у)., то функция f (х, у) имеет минимум в точке M0 (x0, y0). Точки, в которых функция принимает максимальное и минимальное значения, называются экстремальными.

Метод наименьших квадратов

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.