Решить дифференциальное уравнение 2-го порядка с постоянными коэффициентами методом неопределенных коэффициентов.
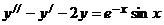 .
.
Составим характеристическое уравнение 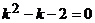 . Оно имеет два различных корня
. Оно имеет два различных корня 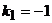 ,
, 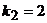 . Поэтому общее решение однородного уравнения
. Поэтому общее решение однородного уравнения 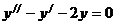 имеет вид
имеет вид 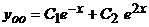 .
.
Правую часть уравнения 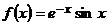 представим в виде
представим в виде 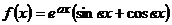 , где
, где 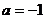 ,
, 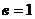 . Комплексное число
. Комплексное число 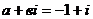 не является корнем характеристического уравнения, поэтому частное решение заданного уравнения запишется в виде
не является корнем характеристического уравнения, поэтому частное решение заданного уравнения запишется в виде 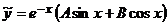 .
.
Для определения А и В найдем 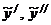 .
.
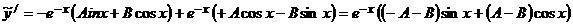
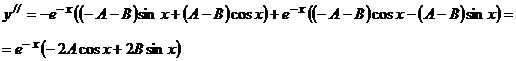
Дальнейшие вычисления оформим следующим образом. Расположим 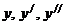 в столбик, слева от них расположим коэффициенты исходного уравнения, после чего составим систему уравнений относительно А и В, приравнивая коэффициенты при
в столбик, слева от них расположим коэффициенты исходного уравнения, после чего составим систему уравнений относительно А и В, приравнивая коэффициенты при 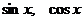 . (на
. (на 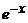 можно сократить). Левой и правой части исходного уравнения.
можно сократить). Левой и правой части исходного уравнения. 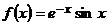 .
.
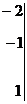
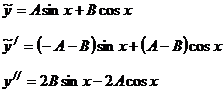
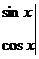
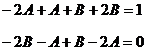
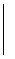
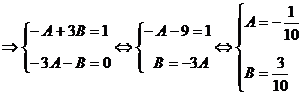
Частное решение запишем 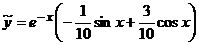 , или
, или 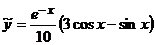 .
.
Общее решение неоднородного уравнения будет
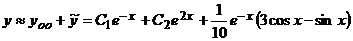
Решить однородное дифференциальное уравнение высшего порядка.
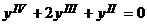
Характеристическое уравнение 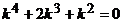 имеет корни
имеет корни 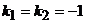 ,
,
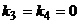 поэтому общее решение однородного дифференциального уравнения
поэтому общее решение однородного дифференциального уравнения 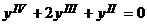 имеет вид
имеет вид 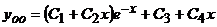
9). Решить дифференциальное уравнение методом вариации произвольных постоянных (методом Лагранжа), удовлетворяющее начальным условиям.
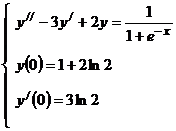
Характеристическое уравнение данного уравнения дифференциального уравнения 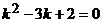 имеет корни
имеет корни 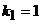 ,
, 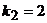 , поэтому общее решение однородного дифференциального уравнения
, поэтому общее решение однородного дифференциального уравнения 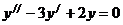 имеет вид
имеет вид 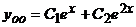
Общее решение заданного неоднородного дифференциального уравнения 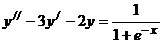 будем искать в виде,
будем искать в виде, 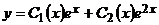 где постоянные
где постоянные 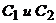 заменим неизвестными функциями
заменим неизвестными функциями 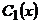 и
и 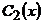 . Неизвестные функции
. Неизвестные функции 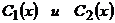 . Найдем из системы Лагранжа
. Найдем из системы Лагранжа
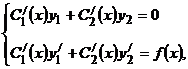 , где
, где 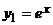 ,
, 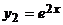 т.е
т.е
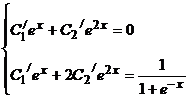
Систему решаем методом Гаусса. Вычтем из 2-го уравнения первое, получим
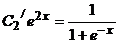 , откуда
, откуда 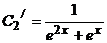 . Интегрируя, найдем
. Интегрируя, найдем 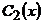
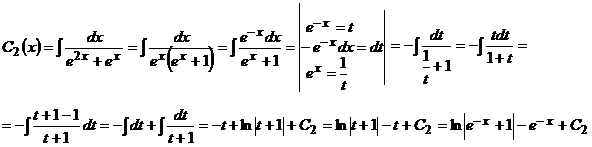
Итак, 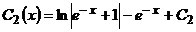
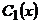 найдем из первого уравнения системы.
найдем из первого уравнения системы.
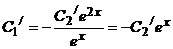 , или
, или 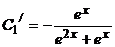 , т.е
, т.е 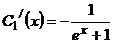 ;
;
Интегрируя, имеем:
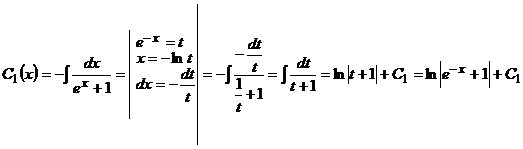 ;
;
или 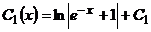 .
.
Общее решение исходного неоднородного уравнения будет 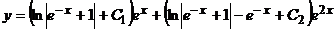 ;
;
или 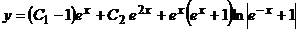 .
.
Решить систему дифференциальных уравнений при начальных условиях.
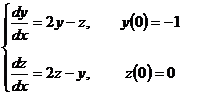
Решить эту систему, означает найти 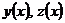 - неизвестные функции от
- неизвестные функции от 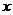 , удовлетворяющие системе дифференциальных уравнений и начальными условиям
, удовлетворяющие системе дифференциальных уравнений и начальными условиям 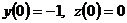 .
.
Нормальную систему можно привести к одному уравнению 2-го порядка относительно одной функции, скажем 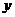 .
.
Дифференцируем первое уравнение системы по 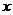 :
:
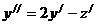 . Вместо
. Вместо 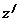 подставим выражение
подставим выражение 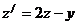 из 2-го уравнения системы
из 2-го уравнения системы 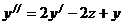 .
.
Вместо z подставим выражение 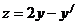 из первого уравнения системы, получим
из первого уравнения системы, получим 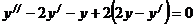 , откуда
, откуда 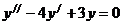 .
.
Характеристическое уравнение данного однородного дифференциального уравнения 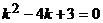 имеет корни
имеет корни 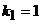 ,
, 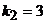 , поэтому общее решение уравнения
, поэтому общее решение уравнения 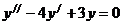 имеет вид
имеет вид 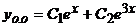 .
.
Чтобы найти функцию 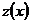 , подставим в 1-е уравнение системы
, подставим в 1-е уравнение системы 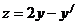
выражение 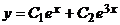 и
и 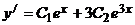 .
.
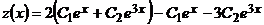 , или
, или 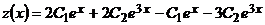 ,
,
откуда 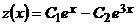 .
.
Таким образом, общее решение системы имеет вид
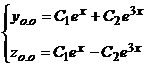 ;
;
Подставляя начальные условия, 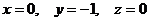 определим контакты
определим контакты
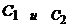 .
. 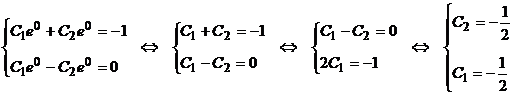
Итак, частные решения, удовлетворяющие начальным условиям, имеет вид
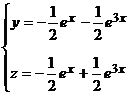
Контрольная работа №7
Ряды. Кратные интегралы.
Задание 1.Исследовать на сходимость, применяя признаки сравнения.
1. 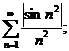
2. 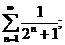
3. 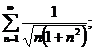
4. 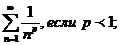
5. 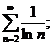
6. 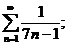
7. 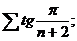
8. 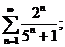
9. 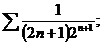
10. 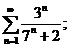
11. 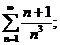
12. 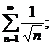
13. 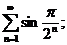
14. 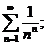
15. 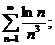
16. 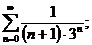
17. 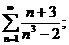
18. 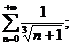
19. 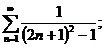
20. 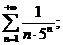
21. 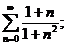
22. 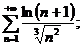
23. 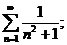
24. 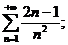
25. 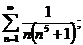
Задание 2.Исследовать на сходимость ряды, применяя признак Коши (радикальный).
1. 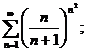
2. 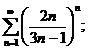
3. 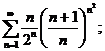
4. 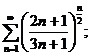
5. 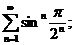
6. 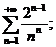
7. 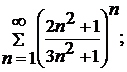
8. 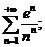
9. 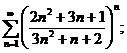
10. 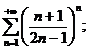
11. 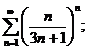
12. 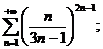
13. 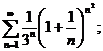
14. 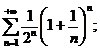
15. 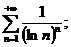
16. 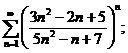
17. 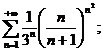
18. 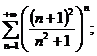
19. 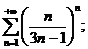
20. 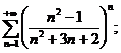
21. 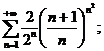
22. 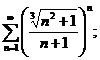
23. 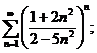
24. 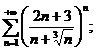
Задание 3.Исследовать на сходимость, применяя признак Даламбера.
1. 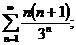
2. 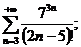
3. 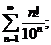
4. 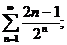
5. 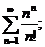
6. 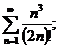
7. 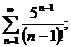
8. 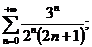
9. 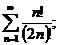
10. 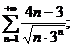
11. 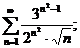
12. 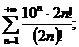
13. 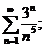
14. 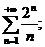
15. 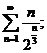
16. 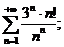
17. 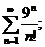
18. 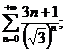
19. 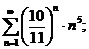
20. 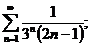
21. 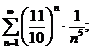
22. 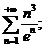
23. 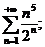
24. 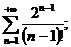
25. 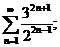
Задание 4.Исследовать на сходимость, применяя интегральный признак Коши.
1. 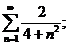
2. 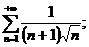
3. 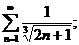
4. 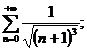
5. 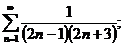
6. 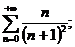
7. 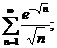
8. 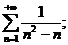
9. 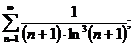
10. 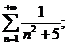
11. 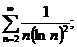
12. 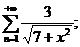
13. 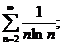
14. 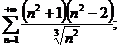
15. 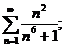
16. 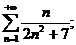
17. 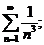
18. 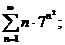
19. 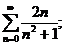
20. 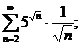
21. 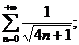
22. 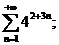
23. 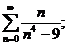
24. 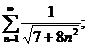
25. 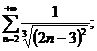
26. 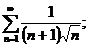
Задание 5.Исследовать на сходимость знакочередующиеся ряды.
1. 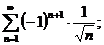
2. 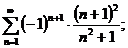
3. 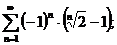
4. 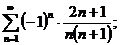
5. 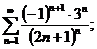
6. 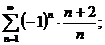
7. 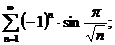
8. 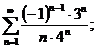
9. 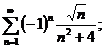
10. 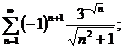
11. 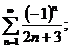
12. 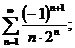
13. 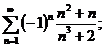
14. 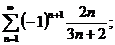
15. 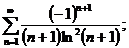
16. 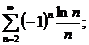
17. 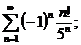
18. 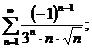
19. 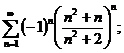
20. 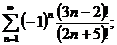
21. 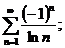
22. 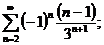
23. 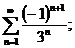
24. 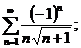
25. 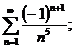
Задание 6.Определить радиус, интервал сходимости и выяснить поведение ряда на концах интервала сходимости.
1. 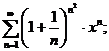
2. 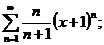
3. 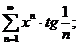
4. 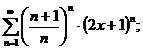
5. 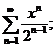
6. 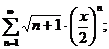
7. 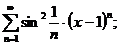
8. 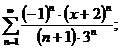
9. 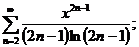
10. 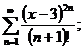
11. 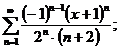
12. 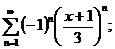
13. 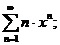
14. 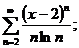
15. 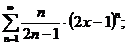
16. 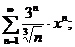
17. 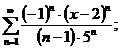
18. 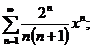
19. 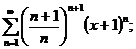
20. 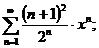
21. 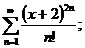
22. 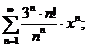
23. 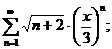
24. 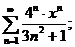
25. 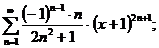
Задание 7.Разложить функции.
1. 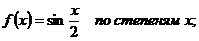
2. 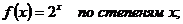
3. 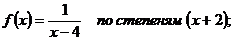
4. 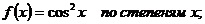
5. 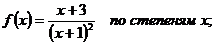
6. 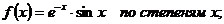
7. 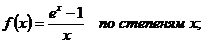
8. 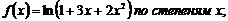
9. 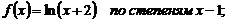
10. 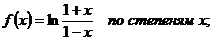
11. 
12. 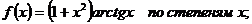
13. 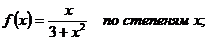
14. 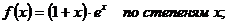
15. 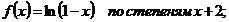
16. 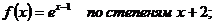
17. 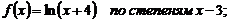
18. 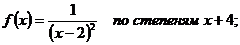
19. 
20. 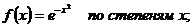
21. 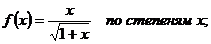
22. 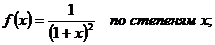
23. 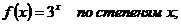
24. 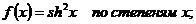
25. 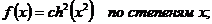
Задание 8.Проинтегрировать, применяя разложение в ряд.
1. 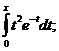
2. 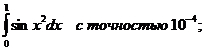
3. 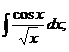
4. 
5. 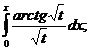
6. 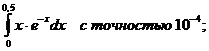
7. 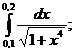
8. 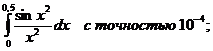
9. 
10. 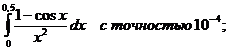
11. 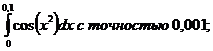
12. 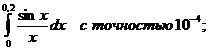
13. 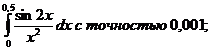
14. 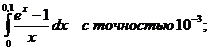
15. 
16. 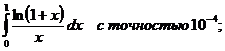
17. 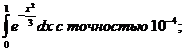
18. 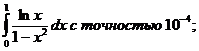
19. 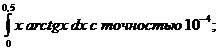
20. 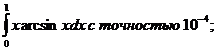
21. 
22. 
23. 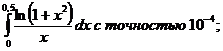
24. 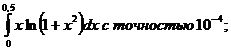
25. 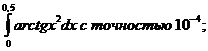
Задание 9.Решить уравнения с помощью степенного ряда.
1. 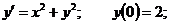
2. 
3. 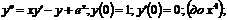
4. 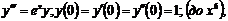
5. 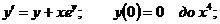
6. 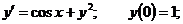
7. 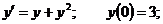
8. 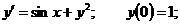
9. 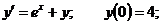
10. 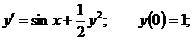
11. 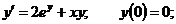
12. 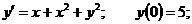
13. 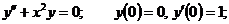
14. 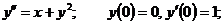
15. 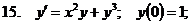
16. 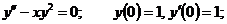
17. 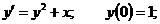
18. 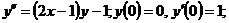
19. 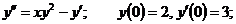
20. 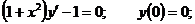
21. 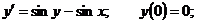
22. 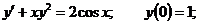
23. 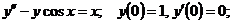
24. 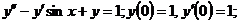
25. 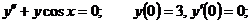
Задание 10.Вычислить с точностью до 0,0001.
1. 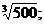
2. 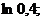
3. 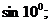
4. 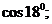
5. 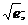
6. 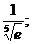
7. 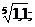
8. 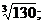
9. 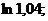
10. 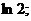
11. 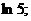
12. 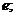
13. 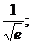
14. 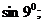
15. 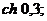
16. 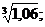
17. 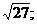
18. 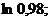
19. 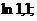
20. 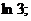
21. 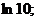
22. 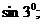
23. 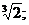
24. 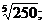
25. 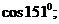
Задание 11. Вычислить двойной интеграл по области D, ограниченной линиями.
1. 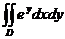 , D:
, D: 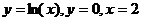 .
.
2. 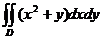 , D:
, D: 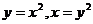 .
.
3. 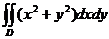 , D:
, D: 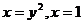 .
.
4. 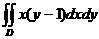 , D:
, D: 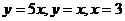 .
.
5. 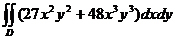 , D:
, D: 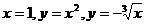 .
.
6. 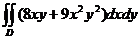 , D:
, D: 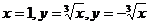 .
.
7. 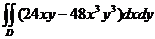 , D:
, D: 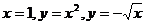 .
.
8. 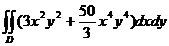 , D:
, D: 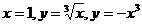 .
.
9. 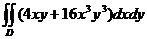 , D:
, D: 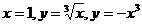 .
.
10. 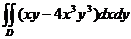 , D:
, D: 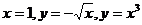 .
.
11. 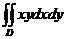 , D:
, D: 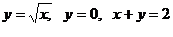 .
.
12. 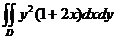 , D:
, D: 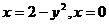 .
.
13. 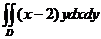 , D:
, D: 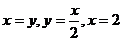 .
.
14. 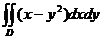 , D:
, D: 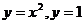 .
.
15. 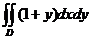 , D:
, D: 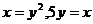 .
.
16. 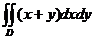 , D:
, D: 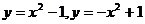 .
.
17. 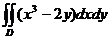 , D:
, D: 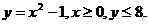
18. 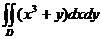 , D:
, D: 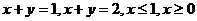 .
.
19. 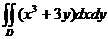 , D:
, D: 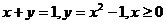 .
.
20. 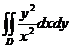 , D:
, D: 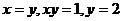 .
.
21. 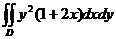 , D:
, D: 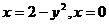 .
.
22. 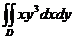 , D:
, D: 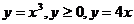 .
.
23. 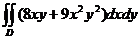 , D:
, D: 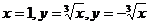 .
.
24. 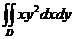 , D:
, D: 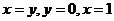 .
.
25. 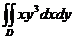 , D:
, D: 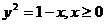 .
.
26. 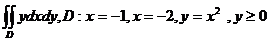 .]
.]
27. 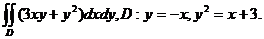
28. 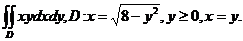
29. 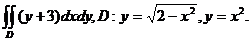
30. 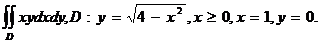
Задание 12. Вычислить двойной интеграл, используя переход к полярным координатам.
1. 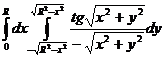 .
.
2. 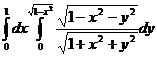 .
.
3. 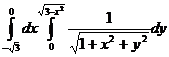 .
.
4. 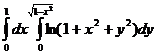 .
.
5. 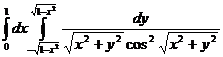 .
.
6. 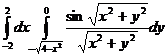 .
.
7. 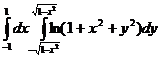 .
.
8. 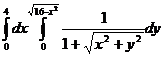 .
.
9. 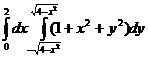 .
.
10. 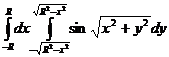 .
.
11. 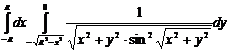 .
.
12. 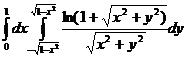 .
.
13. 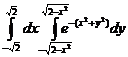 .
.
14. 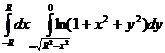 .
.
15. 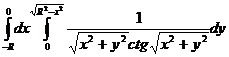 .
.
16. 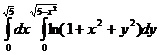 .
.
17. 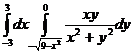 .
.
18. 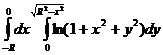 .
.
19. 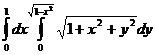 .
.
20. 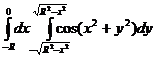 .
.
21. 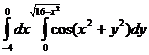 .
.
22. 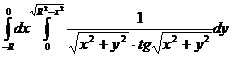 .
.
23. 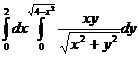 .
.
24. 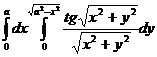 .
.
25. 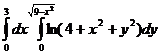 .
.
26. 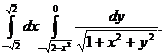
27. 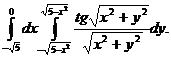
28. 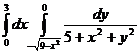 .
.
29. 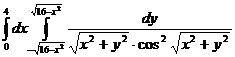 .
.
30. 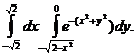
Задание 13. Вычислить площадь плоской области D, ограниченной указанными линиями.
1. 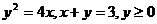 .
.
2. 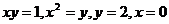 .
.
3. 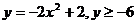 .
.
4. 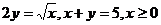 .
.
5. 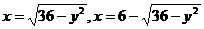 .
.
6. 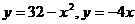 .
.
7. 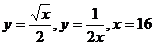 .
.
8. 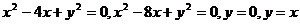
9. 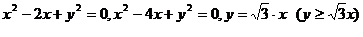
10. 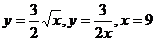 .
.
11. 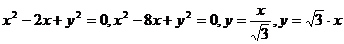 .
.
12. 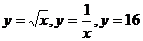 .
.
13. 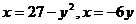 .
.
14. 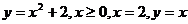 .
.
15. 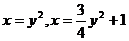 .
.
16. 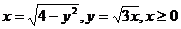 .
.
17. 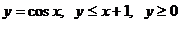 .
.
18. 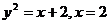 .
.
19. 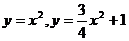 .
.
20. 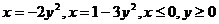 .
.
21. 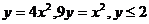 .
.
22. 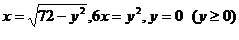 .
.
23. 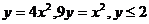 .
.
24. 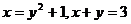 .
.
25. 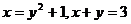 .
.
26. 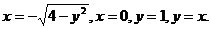
27. 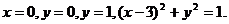
28. 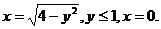
29. 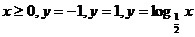 .
.
30. 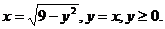
Задание 14. Вычислить объем тела, ограниченного заданными поверхностями.
1. 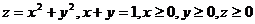 .
.
2. 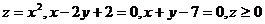 .
.
3. 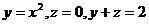 .
.
4. 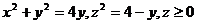 .
.
5. 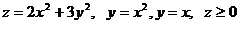 .
.
6. 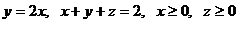 .
.
7. 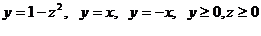 .
.
8. 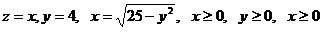 .
.
9. 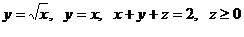 .
.
10. 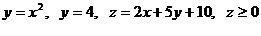 .
.
11. 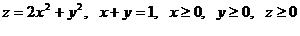 .
.
12. 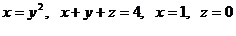 .
.
13. 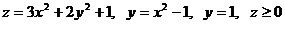 .
.
14. 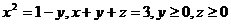 .
.
15. 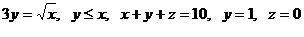 .
.
16. 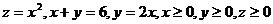 .
.
17. 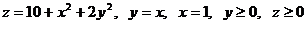 .
.
18. 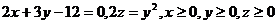 .
.
19. 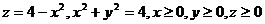 .
.
20. 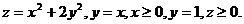
21. 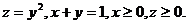
22. 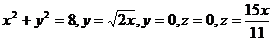 .
.
23. 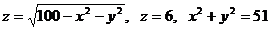 .
.
24. 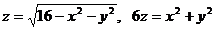 .
.
25. 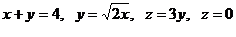 .
.
26. 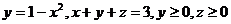 .
.
27. 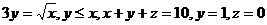 .
.
28. 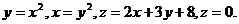
29. 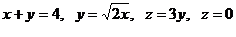 .
.
30. 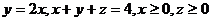 .
.
Задание 15. Вычислить массу неоднородной пластинки D, ограниченной указанными линиями, если поверхностная плотность в каждой её точке равна 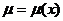
1. 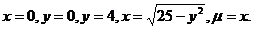
2. 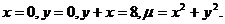
3. 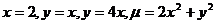 .
.
4. 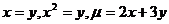 .
.
5. 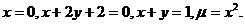
6. 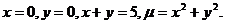
7. 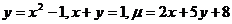 .
.
8. 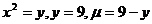 .
.
9. 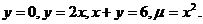
10. 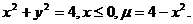
11. 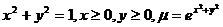 .
.
12. 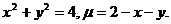
13. 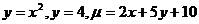 .
.
14. 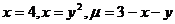 .
.
15. 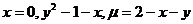 .
.
16. 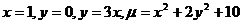 .
.
17. 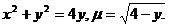
18. 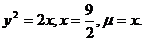
19. 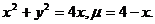
20. 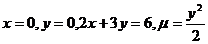 .
.
21. 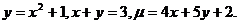
22. 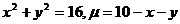 .
.
23. 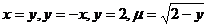 .
.
24. 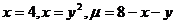 .
.
25. 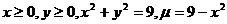 .
.
26. 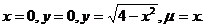
27. 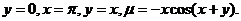
28. 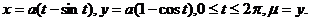
29. 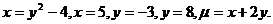
Задание 16. Расставить пределы интегрирования в тройном интеграле 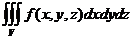 , если область интегрирования V ограничена заданными поверхностями. Начертите область V.
, если область интегрирования V ограничена заданными поверхностями. Начертите область V.
1. 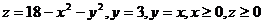 .
.
2. 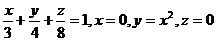 .
.
3. 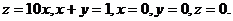
4. 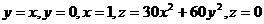 .
.
5. 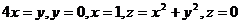 .
.
6. 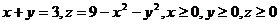 .
.
7. 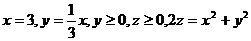 .
.
8. 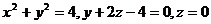 .
.
9. 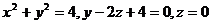 .
.
10. 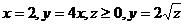 .
.
11. 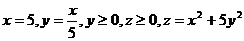 .
.
12. 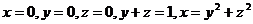 .
.
13. 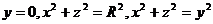 .
.
14. 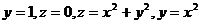 .
.
15. 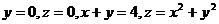 .
.
16. 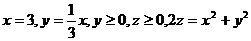 .
.
17. 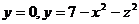 .
.
18. 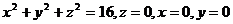 .
.
19. 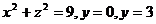 .
.
20. 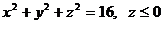 .
.
21. 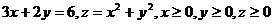 .
.
22. 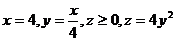 .
.
23. 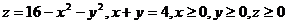 .
.
24. 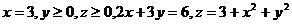 .
.
25. 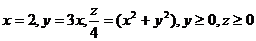 .
.
26. 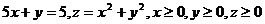 .
.
27. 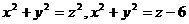 .
.
28. 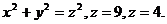
29. 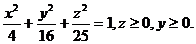
30. 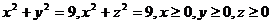 .
.
Задание 17. Вычислить координаты центра масс однородного тела, занимающего область V, ограниченную указанными поверхностями.
1. 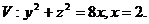
2. 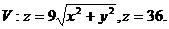
3. 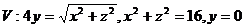 .
.
4. 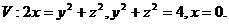
5. 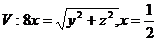 .
.
6. 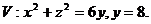
7. 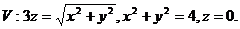
8. 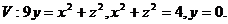
9. 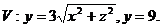
10. 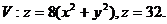
11. 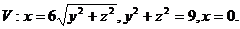
12. 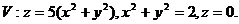
13. 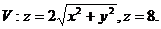
14. 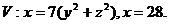
15. 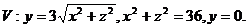
16. 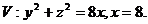
17. 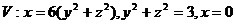 .
.
18. 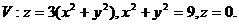
19. 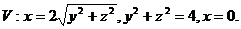
20. 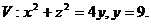
21. 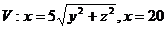 .
.
22. 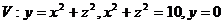 .
.
23. 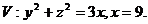
24. 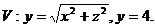
25. 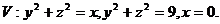
26. 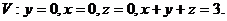
27. 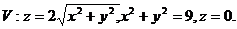
28. 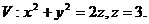
29. 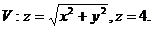
30.
