Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Это будет уравнение вида

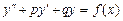. (8)

Теорема. Общее решение Y линейного неоднородного дифференциального уравнения с постоянными коэффициентами

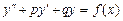
есть сумма его частного решения 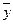и общего решения 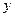соответствующего однородного уравнения (6), т. е. Y = y + .

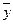В некоторых случаях частное решение 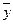уравнения (8) можно найти по виду правой части f(x).

1. f(x) = 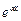· P_n(x),

где P_n(x) — многочлен n-й степени и число 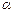не является корнем характеристического уравнения однородного уравнения (6). Тогда частное решение 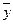следует искать в виде

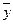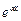= · Q_n(x),

где Q_n(x) — многочлен n-й степени, но с неопределенными коэффициентами.

Если же 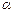— корень характеристического уравнения кратности r, то частное решение ищут в виде

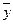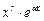= · Q_n(x).

2. f(x) = 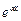(a · cos 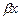+ b · sin 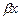), 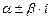не являются корнями характеристического уравнения. Тогда частное решение 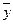ищут в виде

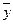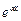= (A · cos 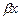+ B · sin ),

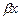где A, B — некоторые неопределенные коэффициенты.

Если же 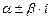— корни характеристического уравнения, то частное решение ищут в виде

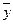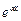= x · · (A · cos 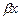+ B · sin ).

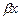Вопросы для самопроверки

1. Что называется обыкновенным дифференциальным уравнением? Приведите примеры.

2. Что называется общим решением дифференциального уравнения n-го порядка? Что такое частное решение этого уравнения?

3. Где применяются дифференциальные уравнения в области экономики? Приведите примеры.

4. В чем состоит задача Коши для дифференциального уравнения первого порядка, разрешенного относительно производной? Опишите геометрическую интерпретацию этой задачи.

5. Какое дифференциальное уравнение называется уравнением с разделяющимися переменными? Как оно решается?

6. Какое уравнение называется линейным неоднородным уравнением первого порядка и как оно решается?

7. Что называется линейным однородным дифференциальным уравнением второго порядка? Какими свойствами обладает общее решение этого уравнения?

8. Каким образом решается линейное однородное уравнение второго порядка с постоянными коэффициентами?

9. Что называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами? Какова структура его общего решения?

10. Какие вы знаете случаи нахождения частного решения 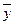неоднородного уравнения по виду его правой части?

Типовая задача 6

Найти общее решение дифференциального уравнения 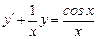и частное решение, удовлетворяющее начальному условию .

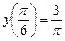Решение. Это линейное неоднородное дифференциальное уравнение первого порядка решаем методом Бернулли. Полагаем, что y = u · v, где u, v — некоторые неизвестные пока функции. Тогда y' = u' · v + u · v'. Подставляя в данное уравнение вместо y, y' их указанные значения, получим:

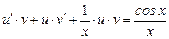
или

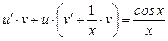. (9)

Выберем функцию 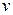таким образом, чтобы выполнялось равенство .

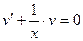Отсюда, учитывая, что 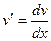, представим уравнение в виде

.

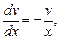
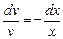Интегрируем: .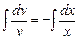

Отсюда

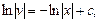
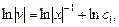где с = lnc₁ ,

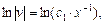
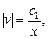
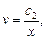где с₂ = 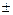c₁ .

Пусть с₂ = 1. Тогда .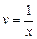

Подставляя полученное значение функции v в формулу (9),
получим:

= , ,

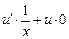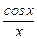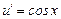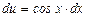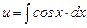, , u = sin x + C.

Таким образом, 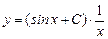— общее решение данного дифференциального уравнения.

Теперь решаем задачу Коши. Подставляем в формулу общего решения вместо х, у соответственно числа :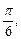

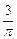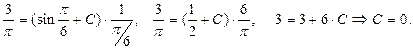
Итак, 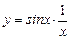— частное решение данного дифференциального уравнения, удовлетворяющее поставленному начальному условию.

Ответ: , .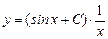

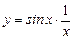Типовая задача 7

Найти общее решение дифференциального уравнения y'' – 5y' + 4y =
= x² – 1.

Решение. Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решаем однородное уравнение y'' – 5y' + 4y = 0. Для этого составляем характеристическое уравнение k² – 5k + 4 = 0, откуда k₁ = 1, k₂ = 4.

Тогда y = C₁ · e^x + C₂ · e^4x — общее решение однородного уравнения.

Находим частное решение 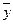неоднородного уравнения. Его будем искать в виде .

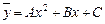Тогда 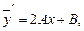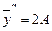. Подставляя полученные значения 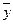, , 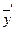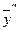в исходное уравнение, будем иметь:

2A – 10Ax – 5B + 4Ax² + 4Bx + 4C = x² – 1,

или

4Ax² + (4B – 10A) · x + 2A – 5B + 4C = x² – 1.

Два многочлена между собой равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях. Отсюда

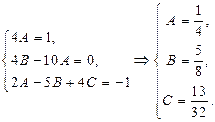
Таким образом,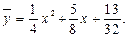

Итак, 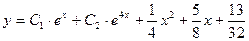— общее решение данного неоднородного уравнения.

Ответ: 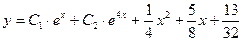.