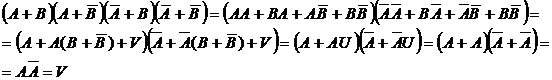Функции от случайных величин

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента: .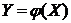

Если Х – дискретная случайная величина, а функция 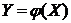- монотонна, то различным значениям Х соответствует различные значения Y, а вероятности соответствующих значений Х и Y равны:

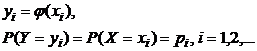
Если 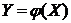- немонотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y, для которых вероятности находятся, как суммы вероятностей соответствующих значений Х:

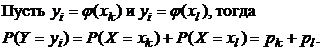
Если Х – непрерывная случайная величина с плотностью распределения f(x), а функция 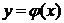- дифференцируемая монотонная функция, то для отыскания плотности распределения g(y) случайной величины Y находят:

1. функцию 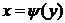, обратную функции ;

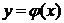2. функцию ;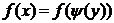

3. производную .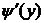

Тогда плотность распределения g(y) случайной величины Y будет равна:

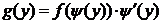. (37)

Если каждой паре возможных значений случайных величин Х и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов Х и Y: 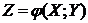, [4, c. 207].

Пусть Z = Х + Y. Тогда для отыскания значений Z находят всевозможные суммы значений Х и Y (в случае произведения Х и Y – всевозможные произведения значений, в случае разности – всевозможные разности). Если Х и Y независимы, то вероятности значений Z (в любом из указанных случаев) находят как произведения вероятностей соответствующих значений Х и Y. Таким образом, если z_i = x_j + y_k, то p(z_i) = p(x_j)∙p(y_k) (аналогично, если z_i = x_j ∙ y_k или z_i = x_j – y_k).

Закон распределения двумерной дискретной случайной величины можно так же, как и при распределении одномерной дискретной случайной величины, задать аналитически и с помощью таблицы.

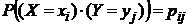(20)

Таблица 5 – Закон распределения двумерной дискретной случайной величины (Х,Y)

уj xi	у1	у2	…	уj	…	уm	Вероятности значений Х
x1	p11	p12	…	p1j	…	p1m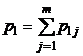
x2	p21	p22	…	p2j	…	p2m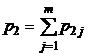
…	…	…	…	…	…	…
xi	pi1	pi2	…	pij	…	pim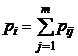
…	…	…	…	…	…	…
xn	pn1	pn2	…	pnj	…	pnm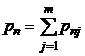
Вероятности значений Y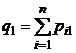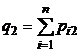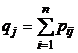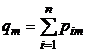

В последнем столбце таблицы 5 указаны вероятности значений случайной величины X, а в последней строке – вероятности значений случайной величины Y. Найденные значения вероятностей каждой из случайных величин позволят составить соответствующие этим величинам законы распределения, [5, c. 124].

В случае отыскания условных законов распределения можно воспользоваться формулой (39), подставляя в неё соответствующие определённым условиям значения вероятностей. В формуле (39) приведены вероятности событий 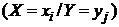. Каждое из них заключается в том, что величина X принимает некоторое конкретное значение 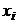при условии, что Y принимает заранее определённое значение .

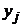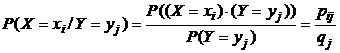. (21)

Используя формулу (21) получим условный закон распределения величины X при условии, что Y принимает значение 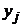(табл. 6). При этом .

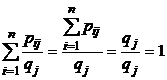Таблица 6 – Условный закон распределения случайной величины Х

Х	x1	x2	…	xi	…	xn
			…		…

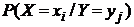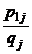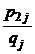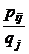Функция распределения двумерной дискретной случайной величины определяется по формуле: 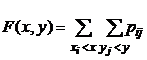. Её свойства аналогичны свойствам функции распределения одномерной случайной величины и вытекают из них.

Функция распределения двумерной непрерывной случайной величины может быть найдена через её плотность распределения по формуле (40).

Плотность распределения двумерной непрерывной случайной величины f(x,y) имеет свойства, вытекающие из свойств функции распределения одномерной случайной величины. Для f(x,y) выполняется:

1. .

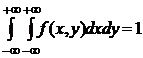2.

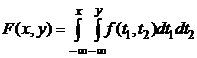
3. .

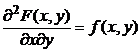4. Вероятность попадания случайной точки (x, y), каждая координата которой принадлежит множеству действительных чисел R, в область 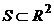равна .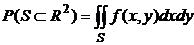

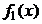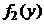5. Плотности распределения и случайных величин соответственно Х и Y двумерной случайной величины (Х , Y) можно получить, зная плотность распределения f(x,y):

;

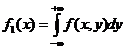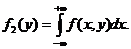
ПРИМЕРЫ ЗАДАЧ С РЕШЕНИЯМИ

2.1 Задачи на основные понятия и теоремы теории вероятностей

Задача 2.1.1

Покупатель приобрёл телевизор и магнитофон. Вероятность того, что в течение гарантийного срока не выйдет из строя телевизор, равна 0,85, а для магнитофона она равна 0,98. Найти вероятность того, что

а) оба они выдержат гарантийный срок службы;

б) хотя бы один из них не выдержит гарантийного срока службы.

Решение:

Рассмотрим события:

А - в течение гарантийного срока не выйдет из строя телевизор,

В - в течение гарантийного срока не выйдет из строя магнитофон.

По условию задачи

Р(А) = 0,85; Р(В) = 0,98.

а) Пусть событие С заключается в том, что оба они выдержат гарантийный срок службы, тогда С = А· В.

Так как события А и В независимы, то по теореме (13) умножения вероятностей Р(С) = Р(А)· Р(В). То есть Р(С) = 0,85· 0,98 = 0,833 ≈ 83 %.

б) Пусть событие D заключается в том, что хотя бы одно изделие не выдержит гарантийного срока службы. Тогда событие 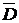означает, что оба изделия будут исправны:

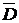= С = А· В, Р( 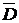) = 0,833. Найдём P(D):

P(D) = 1 – P( 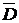) = 1 - 0,833 = 0,167 ≈ 17 %.

Ответ: а) вероятность того, что оба изделия выдержат гарантийный срок службы, равна 83 %; б) вероятность того, что хотя бы одно из них не выдержит гарантийного срока службы, равна 17%.

Задача 2.1.2

Предполагая, что для шахматиста в каждой партии равновероятны три исхода: выигрыш, ничья и проигрыш, найти вероятность того, что из четырёх партий шахматист

а) не проиграет ни одной партии;

б) проиграет хотя бы две партии.

Решение:

а) Рассмотрим события: Н₁ – выигрыш, Н₂ – ничья, Н₃ – проигрыш, В – шахматист не проиграет ни одной партии; В_i – шахматист не проиграет i - ую партию, i = 1, 2, 3, 4.

При этом, В_i = Н₂ + Н₃, а В = В₁ ·В₂ ·В₃ ·В₄. Так как события В_i независимы, то согласно формуле (13), Р(В) =Р(В₁)·Р(В₂)·Р(В₃)·Р(В₄).

Найдём вероятности событий В_i:

По условию задачи Р(Н₁)=Р(Н₂)=Р(Н₃), а так как эти события образуют полную группу в случае одной партии, то вероятность каждого из них р = 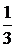. Тогда, согласно формуле (10), так как события Н₂ и Н₃ несовместны, Р(В_i)= 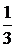+ 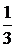= 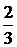. Следовательно,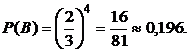

б) Пусть события С_i означают проигрыш i партий, i = 0, 1, 2, 3, 4. Тогда событие С – проиграть хотя бы две партии – можно выразить следующим образом:

.

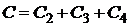Событием, противоположным С, будет событие 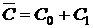, при этом 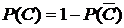. Найдём вероятность 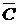. Так как события 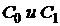несовместны, по теореме сложения вероятностей (10) получим:

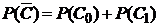. При этом

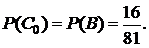
Так как 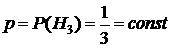для каждой парии, а все партии – независимые испытания, то для отыскания 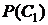можно использовать формулу Бернулли (16):

.

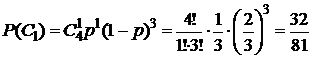Тогда

а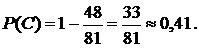

Ответ: а) вероятность того, что из четырёх партий шахматист не проиграет ни одной партии, равна 20%; б) вероятность того, что из четырёх партий шахматист проиграет хотя бы две партии, равна 41%.

Задача 2.1.3 (о встрече)

Двое приятелей договорились встретиться с 10 до 11 часов в определенном месте, причём пришедший первым ждет в течение 20 минут, после чего уходит. Найти вероятность встречи.

Решение:

Пусть событие А соответствует встрече. Если за х обозначить время прихода первого товарища, а за у – второго, то условие их встречи можно задать системой неравенств:

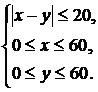
На плоскости хОу область 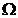, соответствующая общему числу исходов, будет определена системой 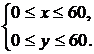, а область D, соответствующая числу исходов, благоприятствующих событию А, определяется неравенством 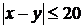(рисунок 1).

Из последнего неравенства получим:

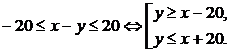
Тогда по определению геометрической вероятности (8), вероятность события А будет равна:

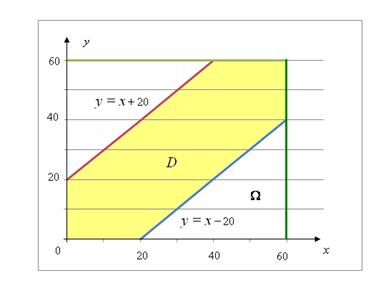
Рисунок 1 – Области для отыскания геометрической

вероятности в задаче 2.1.3

Ответ: вероятность встречи равна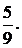

Задача 2.1.4

Доказать, что для событий А и В выполняется: 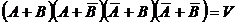, где 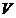- невозможное событие.

Решение:

По свойствам действий над событиями (стр. 9) получим: