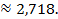Дифференциальные уравнения с разделяющимисяпеременными

Определение:Дифференциальное уравнение с разделяющи-мися переменными имеет вид

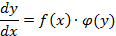
Алгоритм решения:

1) Разделим переменные: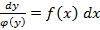

2) Интегрируем обе части равенства: ,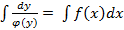

после чего находим общее решение данного дифференциального уравнения в виде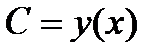

Пример 1: Найти общеерешение дифференциального уравнения: соs²y·ctgxdx + sin²x tgydy=0.

Решение:

Разделим на cos²y·sin²y

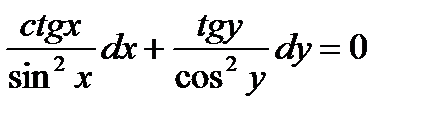, переменные разделены.

Проинтегрируем обе части полученного равенства.

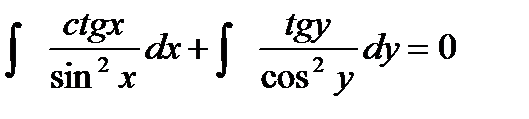
Интегралы находим методом подстановки.

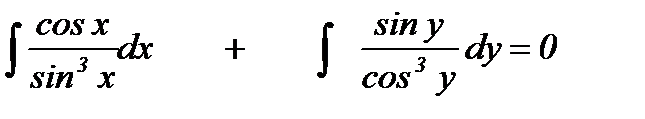
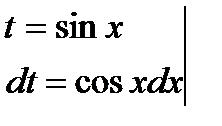
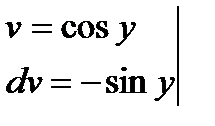
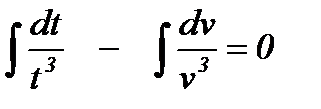
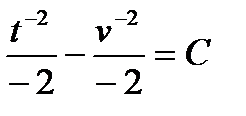или

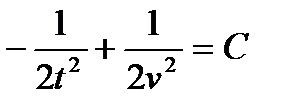
Произведя обратную подстановку, получим:

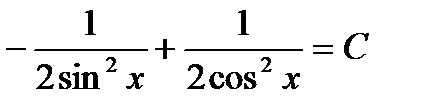или 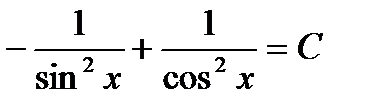Отсюда,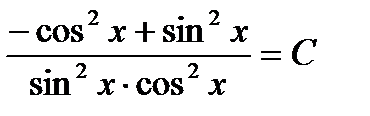

Ответ: 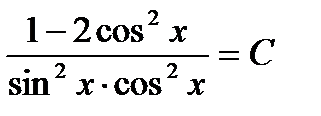- общее решение уравнения.

Пример 2:Найти частное решение дифференцированного уравнения первого порядка

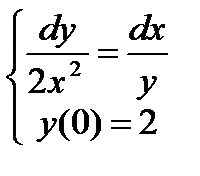
Решение:

Производим разделение переменных:

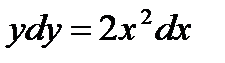
Интегрируя обе части равенства, получаем:

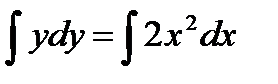
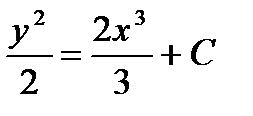
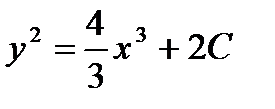
Используя начальное условие, вычислим, соответствующее ему значение постоянное С: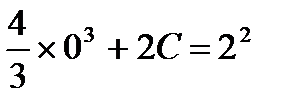

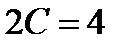
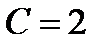
Поэтому частное решение исходного дифференцированного уравнения, удовлетворяющее заданному начальному условию, имеет вид:

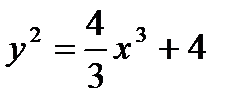
Ответ: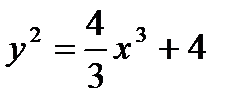

Однородные дифференциальные уравнения

Первого порядка

Определение:Однородной функцией переменных x и y называется функция, все члены которой имеют одинаковую степень.

Например, 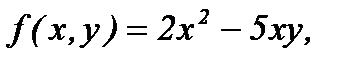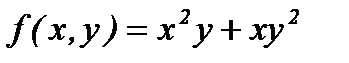- однородные функции второй и третьей степени соответственно.

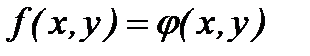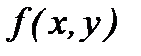Определение:Уравнение вида , где и 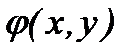- однородные функции одной и той же степени, называетсяоднородным дифференциальным уравнением первого порядка.

Однородное уравнение приводится к уравнению с разделяющими переменными подстановкой, где 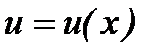– новая искомая функция.

Пример 1: Найти общее решение уравнения

.

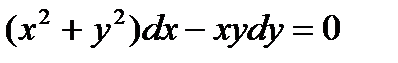Решение:Положим 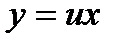. Дифференцируя равенство y = ux, получим 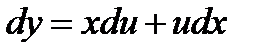. Подставляя выражения в уравнение, получим: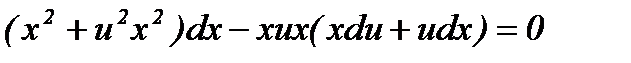

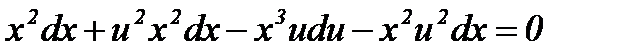
Разделим переменные в полученном уравнении.

;

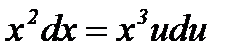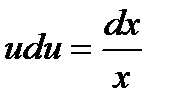
Интегрируем, 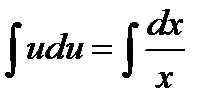. Отсюда, .

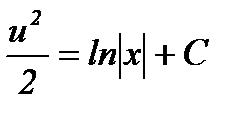Сделаем обратную замену: 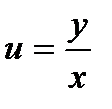, получим .

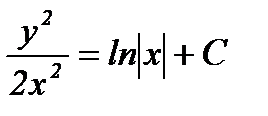Ответ: .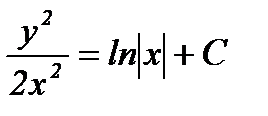

Линейные дифференциальные уравнения

Первого порядка

Определение:Уравнение вида 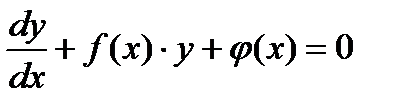называется линейным дифференциальным уравнением первого порядка.В частном случае f (x)и 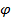(х) могут быть постоянными величинами.

Уравнения такого вида сводятся к двум уравнениям с разделяющимися переменными с помощью подстановки 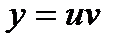, где 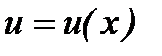, 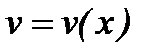- некоторые функции, зависящие от x.

Алгоритм решения:

1) Вводится подстановка 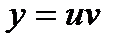, тогда .

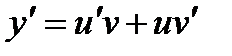2) Исходное уравнение принимает вид:

.

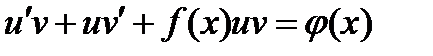3) Группируются слагаемые при u.

.

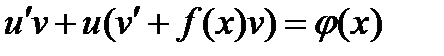4) Выражение в скобках приравнивается к нулю:

.

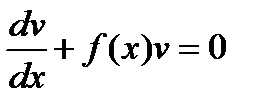Это уравнение с разделяющимися переменными, решая его, находим .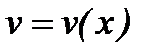

5) Полученное значение v подставляется в выражение:

.

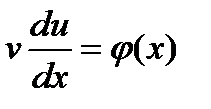Решив уравнение с разделяющимися переменными, получим функцию .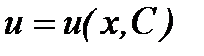

6) Общее решение уравнения запишется в виде:

.

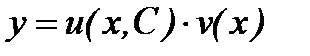Пример 1: Найти общее решение уравнения .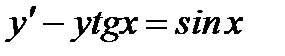

Решение:Обозначим 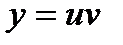, тогда .

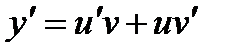Уравнение примет вид .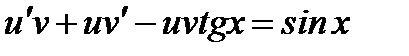

Вынесем во втором и третьем слагаемом общий множитель за скобки, получим .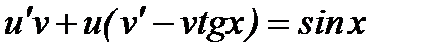

Выражение в скобках приравняем к нулюv′ - vtgx = 0

Перепишем в виде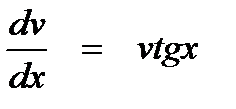

Умножая обе части уравнения на 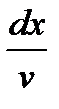, получим ,

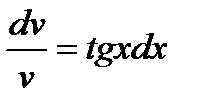интегрируем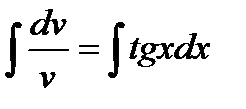

находим 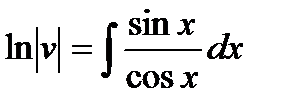, применим замену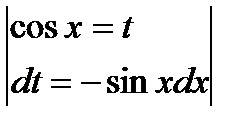

получим ,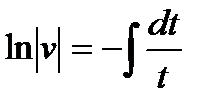

откуда 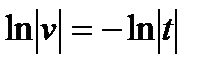или , .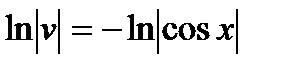

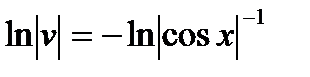Пропотенцируем обе части равенстваv = .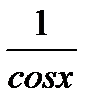

Найденную функцию 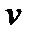подставим в выражение 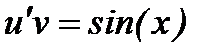и решим полученное уравнение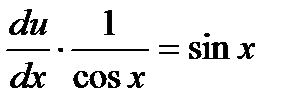

du = sinx∙cos∙xdxили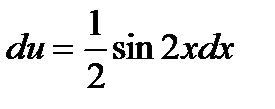

Интегрируем ,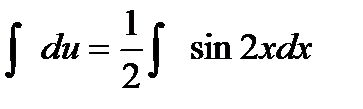

Получим .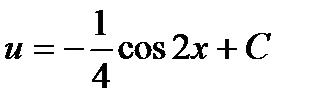

Ответ:Общее решение уравнения у = .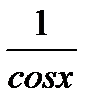

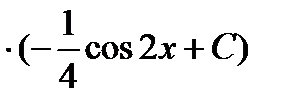Пример 2: Найти частное решение дифференциального уравнения 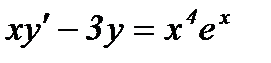, есл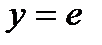и при .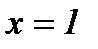

Решение: Пусть 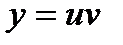, тогда .

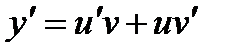Отсюда, .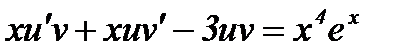

Вынесем u за скобки: .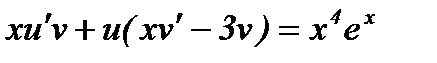

Приравняв скобку к 0 , получим: .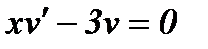

Отсюда, , .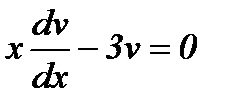

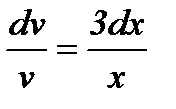Интегрируем ,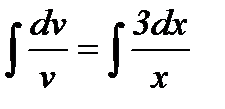

, , .

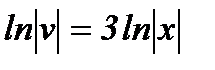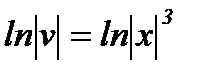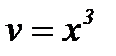Подставив 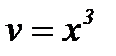в выражение 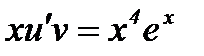, получим уравнение относительно функции u и решим его.

, , , .

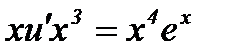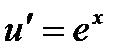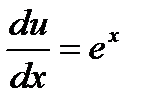Проинтегрируем 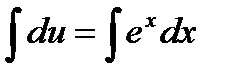. Функция .

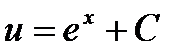Запишем общее решение уравнения : .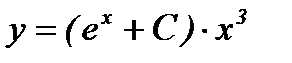

Частное решение найдем из условия 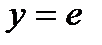при .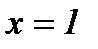

, , .

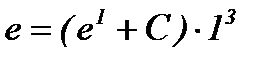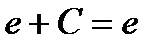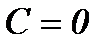Частное решение заданного уравнения имеет вид: .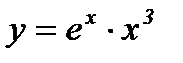

Ответ: 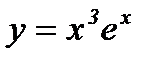- частное решение уравнения.

Понятие числового ряда.

Определение:Числовым рядом называется выражение вида ,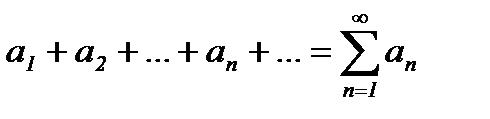

где числа 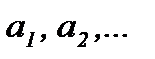– называются членами ряда, член 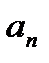– общим членом ряда.

Рядом Тейлора для функции f(x) в точке х₀ называется ряд вида

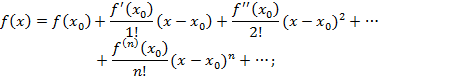
при х₀ = 0 ряд Тейлора называется рядом Маклорена

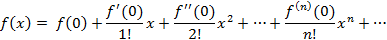
При выполнении приближённых вычислений с помощью рядов:

1) Разложить данную функцию в ряд Тейлора или в ряд Маклорена;

2) Определить, сколько членов ряда надо взять, чтобы получить значение с требуемой точностью;

3) Выполнить вычисления.

Пример 1: Вычислить число е, т.е. значение функции е^х при х = 1, с точностью 0,001 (если известно, что )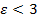

Решение:

Имеем ,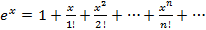

тогда ,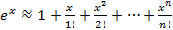

причём абсолютная погрешность этого приближения равна 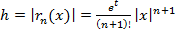, где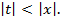

При х = 1 получаем .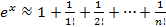

При этом 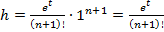, где .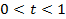

Но так как .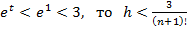

Число n определим из неравенства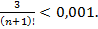

Имеем: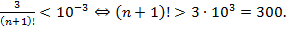

Достаточно взять n = 6, так как (6 + 1)! = 7! = 5040 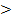3000. Следовательно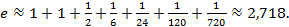

Ответ:e