Плотность распределения вероятностей и числовые характеристики непрерывных случайных величин. Числовые характеристики непрерывных случайных величин

Пример.Непрерывная случайная величина задана функцией распределения

.

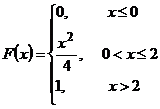Требуется:

а) найти функцию плотности распределения ;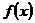

б) найти математическое ожидание 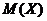, дисперсию 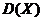и среднее квадратическое отклонение ;

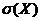в) построить графики функций 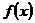и ;

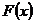г) найти .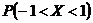

Решение:

а) по определению функции плотности вероятности ¢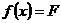

.

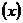
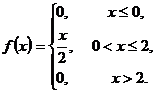б) Для непрерывной случайной величины

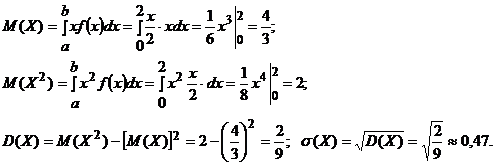
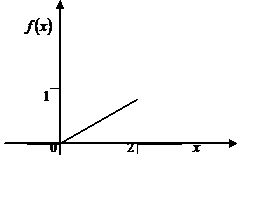в)

г) для вычисления вероятности попадания непрерывной случайной величины в интервал 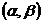можно применить одну из формул:

.

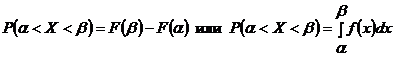Применим первую формулу

.

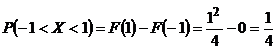Пример.Случайная величина задана плотностью распределения:

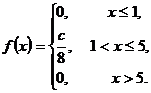
Требуется:

а) найти коэффициент C;

б) функцию распределения ;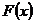

в) построить графики функци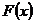й и .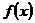

Решение:

а) Плотность распределения 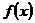должна удовлетворять условиям:

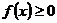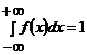; , тогда

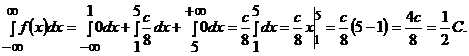
Так как 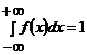, то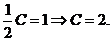

Таким образом,

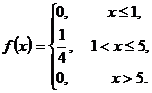
б) для нахождения функции распределения 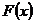воспользуемся формулой

.

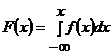При .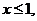

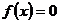
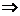
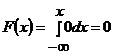При ,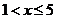

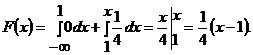
При ,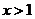

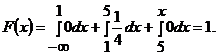
Итак,

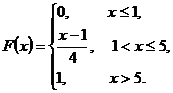
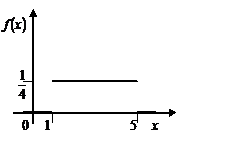Основные законы распределения непрерывных

Случайных величин

Пример. Поезда метро идут строго по расписанию. Интервал движения – 5 минут. Составить f(x) и F(x) случайной величины X – времени ожидания очередного поезда и построить их графики. Найти M(X), D(X).

Решение. Случайная величина X – время ожидания очередного поезда. Величина X распределена равномерно на отрезке [0,5], поэтому воспользуемся формулами

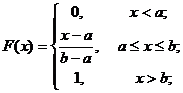
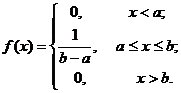
Тогда имеем

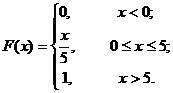
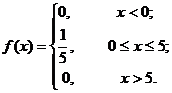
Математическое ожидание и дисперсия вычисляются по формулам:

.

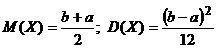Тогда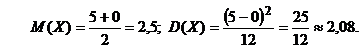

Пример. Непрерывная случайная величина распределена по показательному закону с параметром 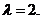Составить функцию распределения, функцию плотности этой случайной величины. Найти числовые характеристики и вероятность того, что случайная величина попадет в интервал (0,3;1).

Решение. Очевидно, искомая плотность распределения

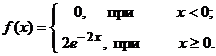
Искомая функция распределения

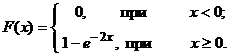
По условию 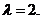Следовательно,

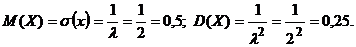
Для нахождения вероятности P(0,3<X<1) воспользуемся формулой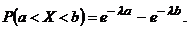

Тогда,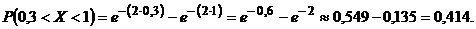

Пример. Детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали равна а=35, среднее квадратическое отклонение 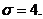Требуется:

а) составить функцию плотности вероятностей;

б) найти вероятность того, что диаметр наудачу взятой детали будет больше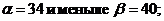

в) найти вероятность того, что диаметр детали отклонится от стандартной длины не больше чем на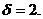

Решение. 1. Так как непрерывная случайная величина X распределена по нормальному закону, есть ее плотность распределения вероятностей выражается формулой

.

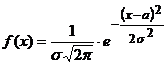Следовательно,

.

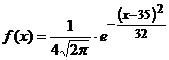2. Для нормально распределенной случайной величины

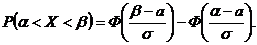
Тогда

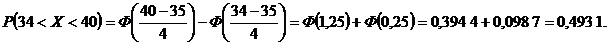3. Последнее задание решаем по формуле

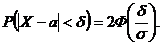
Таким образом,

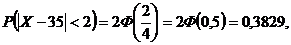
где Ф(x) – интегральная функция Лапласа (табличная).

Закон больших чисел

Пример. Вероятность того, что у отдельного вкладчика некоторого сберегательного банка сумма вклада не больше 3 млн. руб., превышает 0,8. Банк обслуживает 1 000 вкладчиков. Какова общая сумма вкладов этого сберегательного банка?

Решение. 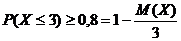. Тогда 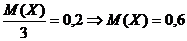. Общая сумма 600 000 000 руб.

Пример. Вероятность того, что студент учебного заведения в период работы читального зала посетит его, равна 0,3. Оценить вероятность того, что среди 900 студентов читального зала посетят от 240 до 300 человек.

Решение. M(X) = np = 900 · 0,3 = 270; D(X) = npq = 189.

Величина отклонения от M(X) равна .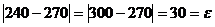

Тогда .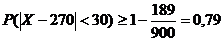

Математическая статистика

Пример. Из большой группы предприятий одной из отраслей промышленности случайным образом отобрано 30, по которым получены показатели основных фондов в млн. руб.: 2; 3; 2; 4; 5; 2; 3; 3; 6; 4; 5; 4; 6; 5; 3; 4; 2; 4; 3; 3; 5; 4; 6; 4; 5; 3; 4; 3; 2; 4.

1. Составить дискретное статистическое распределение выборки.
2. Найти объем выборки.
3. Составить распределение относительных частот.
4. Построить полигон частот.
5. Составить эмпирическую функцию распределения и построить ее график.
6. Найти несмещенные оценки числовых характеристик случайной величины.

Решение

1. Расположим различные значения признака в порядке их возрастания и под каж-

дым из них запишем их частоты. Получим дискретное статистическое распределение выборки:

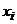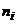где 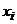- варианты, 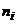- частоты вариант .

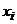2. Сумма частот всех вариант должна быть равной объему выборки.

В данном примере объем выборки равен: n=5 + 8 + 9 + 5 + 3=30.

3. Найдем относительные частоты:

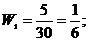
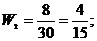
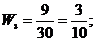
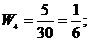
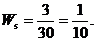
Запишем искомое распределение относительных частот

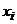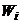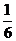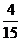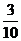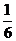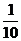Контроль: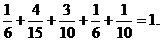

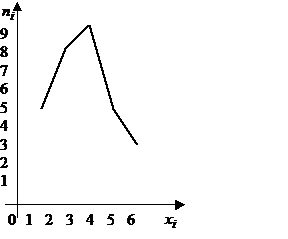
1. 
   Строим точки с координатами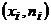 и соединяем их последовательно отрезка-

ми. Полученная ломаная линия называется полигоном частот:

1. Согласно определению эмпирической функцией распределения называется

функция вида

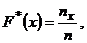
где n – объем выборки; 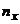- сумма частот вариант, меньших x.

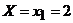Эмпирическая функция является оценкой функции распределения генеральной совокупности. Наименьшая варианта равна 2, поэтому при Значение X<3, а именно, наблюдалось 5 раз. Тогда для 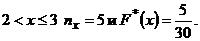Значение X<4, а именно, X=2, X=3, наблюдалось 5 + 8 =13 раз. Поэтому для 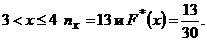Аналогично рассуждая, получаем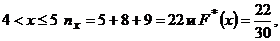: для для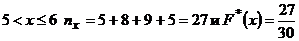

и при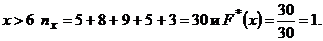

Таким образом,

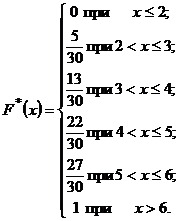
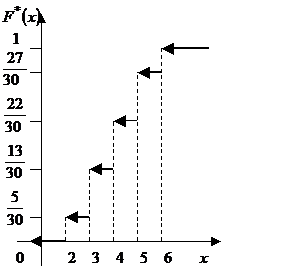График эмпирической функции имеет вид:

1. Несмещенной оценкой математического ожидания является средняя

выборочная:

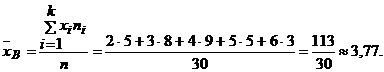
Несмещенная оценка дисперсии – исправления выборочная дисперсия:

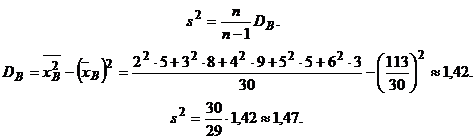
Пример. Выборочно обследование 30 предприятий машиностроительной промышленности по валовой продукции и получены следующие данные, в млн. руб.:

18,0; 12,0; 11,9; 1,9; 5,5; 14,6; 4,8; 5,6; 4,8; 10,9; 9,7; 7,2; 12,4; 7,6;

9,7; 11,2; 4,2; 4,9; 9,6; 3,2; 8,6; 4,6; 6,7; 8,4; 6,8; 6,9; 17,9; 9,6;

14,8; 15,8.

Составить интервальное распределение выборки с началом 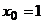и длиной частичного интервала 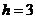. Построить гистограмму частот.

Решение. Для составления интервального распределения составим таблицу, в первой строке которой расположим в порядке возрастания интервалы, длина каждого из которых 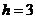. Во второй строке запишем количество значений признака в выборке, попавших в этот интервал (т.е. сумму частот вариант, попавших в соответствующий интервал):

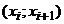	1-4	4-7	7-10	10-13	13-16	16-19

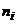Объем выборки n = 2 + 10 + 8 + 5 + 3 + 2 = 30.

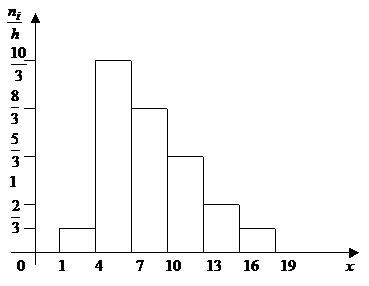Для построения гистограммы частот на оси абсцисс откладываем частичные интервалы, на каждом из них строим прямоугольники высотой 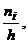где 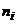- частота i-го частичного интервала, h – шаг (длина интервала), таким образом, гистограмма примет вид:

Указание. Для построения эмпирической функции распределения и нахождения точечных оценок ряда необходимо преобразовать его к дискретному виду по формуле

.

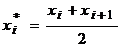Получим

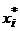	2,5	5,5	8,5	11,5	14,5	17,5

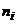Пример. Из большой партии электроламп случайным образом отобрано 100. Средняя продолжительность горения ламп в выборке оказалась равной 1000 ч. Найти с надежностью 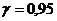доверительный интервал для средней продолжительности а горения ламп во всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы 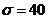ч и продолжительность горения ламп распределена по нормальному закону.

Решение. По условию 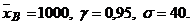Для решения воспользуемся формулой

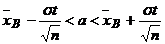
По приложению 3 находим t из условия:

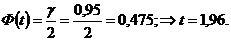
Тогда доверительный интервал:

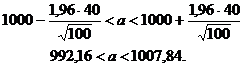
ПРИЛОЖЕНИЯ

Таблица значений функции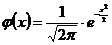

0,0	0,3989
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0	0,2420
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0	0,0450
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0	0,0044
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9

Таблица значений функций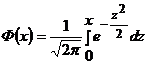

X	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0,00	0,0000	0,43	0,1664	0,86	0,3051	1,29	0,4015
0,01	0,0040	0,44	0,1700	0,87	0,3078	1,30	0,4032
0,02	0,0080	0,45	0,1736	0,88	0,3106	1,31	0,4049
0,03	0,0120	0,46	0,1772	0,89	0,3133	1,32	0,4066
0,04	0,0160	0,47	0,1808	0,90	0,3159	1,33	0,4082
0,05	0,0199	0,48	0,1844	0,91	0,3186	1,34	0,4099
0,06	0,0239	0,49	0,1879	0,92	0,3212	1,35	0,4115
0,07	0,0279	0,50	0,1915	0,93	0,3238	1,36	0,4131
0,08	0,0319	0,51	0,1950	0,94	0,3264	1,37	0,4147
0,09	0,0359	0,52	0,1985	0,95	0,3289	1,38	0,4162
0,10	0,0398	0,53	0,2019	0,96	0,3315	1,39	0,4177
0,11	0,0438	0,54	0,2054	0,97	0,3340	1,40	0,4192
0,12	0,0478	0,55	0,2088	0,98	0,3365	1,41	0,4207
0,13	0,0517	0,56	0,2123	0,99	0,3389	1,42	0,4222
0,14	0,0557	0,57	0,2157	1,00	0,3413	1,43	0,4236
0,15	0,0596	0,58	0,2190	1,01	0,3438	1,44	0,4251
0,16	0,0636	0,59	0,2224	1,02	0,3461	1,45	0,4265
0,17	0,0675	0,60	0,2257	1,03	0,3485	1,46	0,4279
0,18	0,0714	0,61	0,2291	1,04	0,3508	1,47	0,4292
0,19	0,0753	0,62	0,2324	1,05	0,3531	1,48	0,4306
0,20	0,0793	0,63	0,2357	1,06	0,3554	1,49	0,4319
0,21	0,0832	0,64	0,2389	1,07	0,3577	1,50	0,4332
0,22	0,0871	0,65	0,2422	1,08	0,3599	1,51	0,4345
0,23	0,0910	0,66	0,2454	1,09	0,3621	1,52	0,4357
0,24	0,0948	0,67	0,2486	1,10	0,3643	1,53	0,4370
0,25	0,0987	0,68	0,2517	1,11	0,365	1,54	0,4382
0,26	0,1026	0,69	0,2549	1,12	0,3686	1,55	0,4394
0,27	0,1064	0,70	0,2580	1,13	0,3708	1,56	0,4406
0,28	0,1103	0,71	0,2611	1,14	0,3729	1,57	0,4418
0,29	0,1141	0,72	0,2642	1,15	0,3749	1,58	0,4429
0,30	0,1179	0,73	0,2673	1,16	0,3770	1,59	0,4441
0,31	0,1217	0,74	0,2703	1,17	0,3790	1,60	0,4452
0,32	0,1255	0,75	0,2734	1,18	0,3810	1,61	0,4463
0,33	0,1293	0,76	0,2764	1,19	0,3830	1,62	0,4474
0,34	0,1331	0,77	0,2794	1,20	0,3849	1,63	0,4484
0,35	0,1368	0,78	0,2823	1,21	0,3869	1,64	0,4495
0,36	0,1406	0,79	0,2852	1,22	0,3883	1,65	0,4505
0,37	0,1443	0,80	0,2881	1,23	0,3907	1,66	0,4515
0,38	0,1480	0,81	0,2910	1,24	0,3925	1,67	0,4525
0,39	0,1517	0,82	0,2939	1,25	0,3944	1,68	0,4535
0,40	0,1554	0,83	0,2967	1,26	0,3962	1,69	0,4545
0,41	0,1591	0,84	0,2995	1,27	0,3980	1,70	0,4554
0,42	0,1628	0,85	0,3023	1,28	0,3997	1,71	0,4564

Продолжение приложения 3

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
1,72	0,4573	1,94	0,4738	2,32	0,4898	2,76	0,4971
1,73	0,4582	1,95	0,4744	2,34	0,4904	2,78	0,4973
1,74	0,4591	1,96	0,4750	2,36	0,4909	2,80	0,4974
1,75	0,4599	1,97	0,4756	2,38	0,4913	2,82	0,4976
1,76	0,4608	1,98	0,4761	2,40	0,4918	2,84	0,4977
1,77	0,4616	1,99	0,4767	2,42	0,4922	2,86	0,4979
1,78	0,4625	2,00	0,4772	2,44	0,4927	2,88	0,4980
1,79	0,4633	2,02	0,4783	2,46	0,4931	2,90	0,4981
1,80	0,4641	2,04	0,4793	2,48	0,4934	2,92	0,4982
1,81	0,4649	2,06	0,4803	2,50	0,4938	2,94	0,4984
1,82	0,4656	2,08	0,4812	2,52	0,4941	2,96	0,4985
1,83	0,4664	2,10	0,4821	2,54	0,4945	2,98	0,4986
1,84	0,4671	2,12	0,4830	2,56	0,4948	3,00	0,49865
1,85	0,4678	2,14	0,4838	2,58	0,4951	3,20	0,49931
1,86	0,4686	2,16	0,4846	2,60	0,4953	3,40	0,49966
1,87	0,4693	2,18	0,4854	2,62	0,4956	3,60	0,499841
1,88	0,4699	2,20	0,4861	2,64	0,4959	3,80	0,499928
1,89	0,4706	2,22	0,4868	2,66	0,4961	4,00	0,499968
1,90	0,4713	2,24	0,4875	2,68	0,4963	4,50	0,499997
1,91	0,4719	2,26	0,4881	2,70	0,4965	5,00	0,499997
1,92	0,4726	2,28	0,4887	2,72	0,4967
1,93	0,4732	2,30	0,4893	2,74	0,4969