Доверительный интервал для оценки дисперсии и среднего квадратического отклонения.

Требуется оценить неизвестную генеральную дисперсию и генеральное среднее квадратическое отклонение по исправленной дисперсии, т.е. найти доверительные интервалы, покрывающие параметры D и s с заданной надежностью g.

Потребуем выполнения соотношения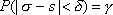

Раскроем модуль и получим двойное неравенство: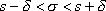

Преобразуем: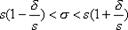

Обозначим d/s = q (величина q находится по "Таблице значений q"и зависит от надежности и объема выборки), тогда доверительный интервал для оценки генерального среднего квадратического отклонения имеет вид: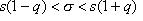

Замечание : Так как s >0, то если q >1 , левая граница интервала равна 0: 0< s < s ( 1 + q ).

Интервальная оценка вероятности биноминального распределения по относительной частоте

Найдем доверительный интервал для оценки вероятности по относительной частоте, используя формулу: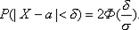

Если n достаточно велико и р не очень близка к нулю и единице, то можно считать, что относительная частота распределена приближенно по нормальному закону, причем М(W)= р. Заменив Х на относительную частоту , математическое ожидание - на вероятность, получим равенство: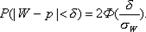

Приступим к построению доверительного интервала (р1, р2), который с надежностью g покрывает оцениваемый параметр р Потребуем, чтобы с надежностью g выполнялось соотношение указанное выше равенство: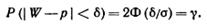

Заменив ,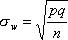

получим: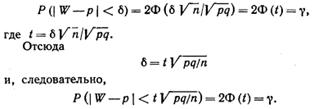

Таким образом, с надежностью g выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1- р вместо q):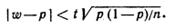

Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда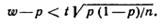

Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно р: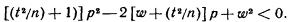

Интервальной оценкой (с надежностью у) неизвестной вероятности р биномиального распределения по относительной частоте w служит доверительный интервал (с приближенными концами p1и р2)

Где P1 < Р < Р2»

Дискриминант трехчлена положительный, поэтому корни действительные и различные:

меньший корень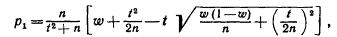

больший корень: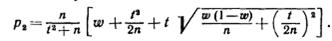

получим приближенные формулы для границ доверительного интервала :

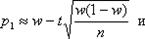
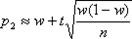
Оценка истинного значения измеряемой величины

Истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. Истинное значение измеряемой величины обычно выступает математическим ожиданием. Поскольку обычно дисперсия неизвестно, следует пользоваться формулами Доверительный интервал для оценки математического ожидания при неизвестном s.

Оценка точности измерений

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения дисперсии случайных ошибок измерений. Для оценки дисперсии используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то теория, Доверительный интервал для оценки дисперсии и среднего квадратического отклонения, применима для оценки точности измерений.