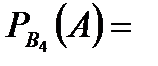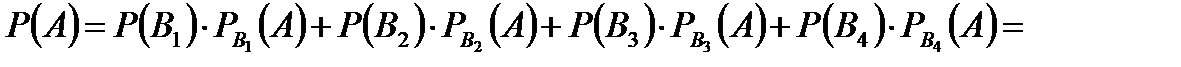Решение задач на применение формулы полной вероятности и формулы Байеса
Число: 2085
| 4.1. Разобрать решение, заполнив пропуски | |||||||||||||||||||||||||||||||
Задача 1.Пешеход, идущий из некоторого пункта  в пункт в пункт 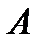 , стоит на разветвлении дорог и выбирает наугад один из возможных путей. Схема дорог изображена на рис. 19. Какова вероятность того, что пешеход попадет в пункт , стоит на разветвлении дорог и выбирает наугад один из возможных путей. Схема дорог изображена на рис. 19. Какова вероятность того, что пешеход попадет в пункт 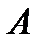 . Решение. . Решение. 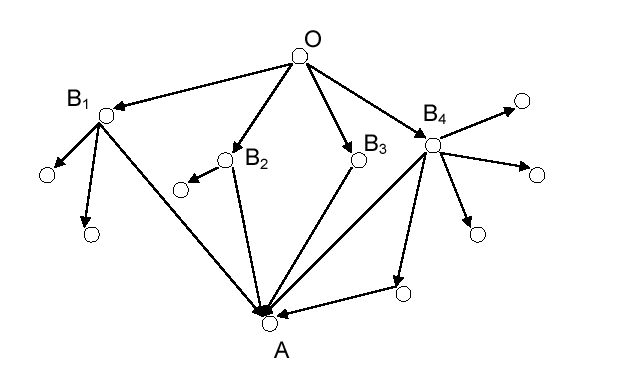
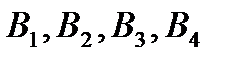 . . Обозначим через Если пешеход попадет в пункт Обозначим через Тогда условная вероятность прийти в Аналогично По формуле полной вероятности
| |||||||||||||||||||||||||||||||
Задача 2. В пирамиде установлены 5 винтовок, из которых 3 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. Решение. Событие 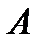 – мишень поражена, из наудачу взятой винтовки. Из условий задачи очевидно, что с рассматриваемым событием связаны гипотезы: – мишень поражена, из наудачу взятой винтовки. Из условий задачи очевидно, что с рассматриваемым событием связаны гипотезы: 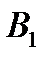 – взята винтовка с оптическим прицелом. – взята винтовка с оптическим прицелом. 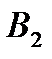 – взята винтовка без оптического прицела. Найдем вероятности гипотез (по классическому определению вероятности): – взята винтовка без оптического прицела. Найдем вероятности гипотез (по классическому определению вероятности): 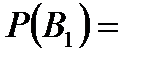 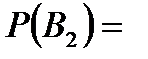 Проверим: Проверим: 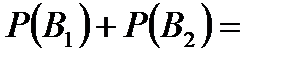 Гипотезы Гипотезы 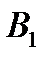 и и 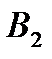 образуют полную группу событий. По условию задачи условные вероятности события A относительно выдвинутых гипотез: образуют полную группу событий. По условию задачи условные вероятности события A относительно выдвинутых гипотез: 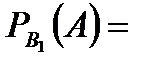 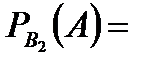 Искомая вероятность равна: Искомая вероятность равна: 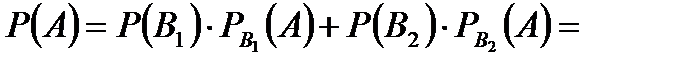 | |||||||||||||||||||||||||||||||
Задача 3.В студенческой группе 20 студентов. Из них 5 отличников, которые знают все экзаменационные вопросы, 8 студентов знают ответы на 70 % вопросов, остальные – на 50 %. Первый вызванный студент ответил на первый вопрос экзаменационного билета. Найти вероятность того, что он отличник. Решение. Будем считать гипотезой 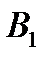 то, что данный отвечающий студент является отличником, то, что данный отвечающий студент является отличником, 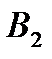 – что он принадлежит ко второй группе, – что он принадлежит ко второй группе, 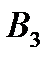 – к третьей. Тогда вероятности гипотез равны (по классическому определению вероятности): – к третьей. Тогда вероятности гипотез равны (по классическому определению вероятности): 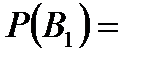 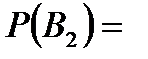 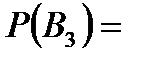 Проверим: Проверим: 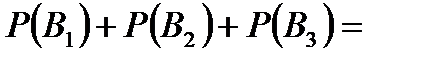 Понятно, что событие Понятно, что событие 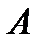 – правильный ответ на первый экзаменационный вопрос – может наступить совместно с одним из трех несовместных событий – правильный ответ на первый экзаменационный вопрос – может наступить совместно с одним из трех несовместных событий 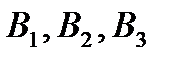 . По условию задачи требуется найти вероятность события . По условию задачи требуется найти вероятность события 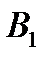 при условии, что произошло событие при условии, что произошло событие 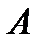 , т.е. , т.е. 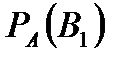 . Применим формулу Байеса: . Применим формулу Байеса: 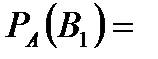 Для этого из условия задачи найдем условную вероятность события Для этого из условия задачи найдем условную вероятность события 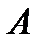 при осуществлении каждой гипотезы и полную вероятность события при осуществлении каждой гипотезы и полную вероятность события 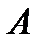 : : 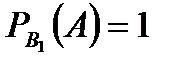 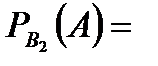 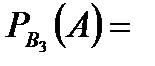 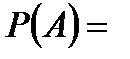 Следовательно, Следовательно, 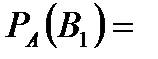 | |||||||||||||||||||||||||||||||
Задача 4.Телеграфное сообщение состоит из сигналов «точка» и «тире». Статистические свойства помех таковы, что искажаются в среднем 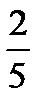 сообщений «точка» и сообщений «точка» и 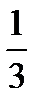 сообщений «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в соотношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если: а) принят сигнал «точка», б) принят сигнал «тире». Решение. Пусть событие сообщений «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в соотношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если: а) принят сигнал «точка», б) принят сигнал «тире». Решение. Пусть событие 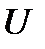 – принят сигнал «точка», а событие – принят сигнал «точка», а событие 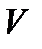 – принят сигнал «тире». Можно сделать две гипотезы: – принят сигнал «тире». Можно сделать две гипотезы: 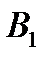 – передан сигнал «точка». – передан сигнал «точка». 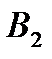 – передан сигнал «тире». По условию задачи требуется найти вероятность события – передан сигнал «тире». По условию задачи требуется найти вероятность события 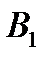 при условии, что произошло событие при условии, что произошло событие 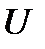 , т.е. , т.е. 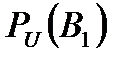 , и вероятность события , и вероятность события 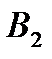 при условии, что произошло событие при условии, что произошло событие 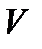 , т.е. , т.е. 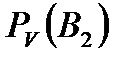 . Применим формулу Байеса: . Применим формулу Байеса: 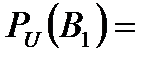 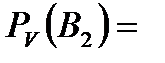 По условию По условию 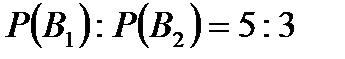 . Но . Но 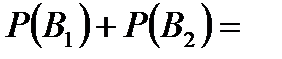 Тогда Тогда 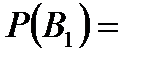 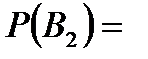 Из условия задачи также известно, что Из условия задачи также известно, что 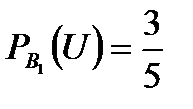 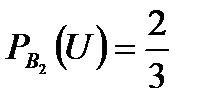 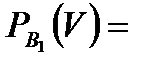 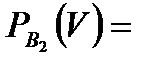 Вероятности событий Вероятности событий 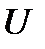 и и 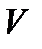 находим по формуле полной вероятности: находим по формуле полной вероятности: 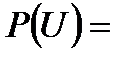 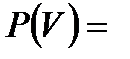 Искомые вероятности будут равны: а) Искомые вероятности будут равны: а) 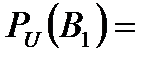 б) б) 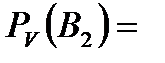 | |||||||||||||||||||||||||||||||
Задача 5.Из 10 каналов радиосвязи 6 каналов защищены от воздействия помех. Вероятность того, что защищенный канал в течение 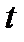 времени не выйдет из строя, равна 0,95, для незащищенного канала – 0,8. Найти вероятность того, что случайно выбранные два канала не выйдут из строя в течение времени не выйдет из строя, равна 0,95, для незащищенного канала – 0,8. Найти вероятность того, что случайно выбранные два канала не выйдут из строя в течение 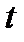 времени, причем оба канала не защищены от воздействия помех. Решение. Пусть событие времени, причем оба канала не защищены от воздействия помех. Решение. Пусть событие 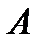 – оба канала не выйдут из строя в течение – оба канала не выйдут из строя в течение 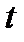 времени. Событие времени. Событие 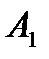 – выбран защищенный канал. Событие – выбран защищенный канал. Событие 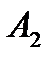 – выбран незащищенный канал. Запишем пространство элементарных событий для опыта – выбрано два канала: – выбран незащищенный канал. Запишем пространство элементарных событий для опыта – выбрано два канала: 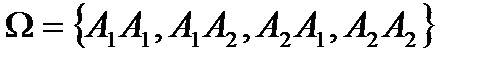 . Возможные гипотезы: . Возможные гипотезы: 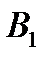 – оба канала защищены от воздействия помех. – оба канала защищены от воздействия помех. 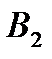 – первый выбранный канал защищен, второй выбранный канал не защищен от воздействия помех. – первый выбранный канал защищен, второй выбранный канал не защищен от воздействия помех. 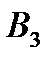 – первый выбранный канал не защищен, второй выбранный канал защищен от воздействия помех. – первый выбранный канал не защищен, второй выбранный канал защищен от воздействия помех. 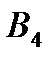 – оба канала не защищены от воздействия помех. – оба канала не защищены от воздействия помех. 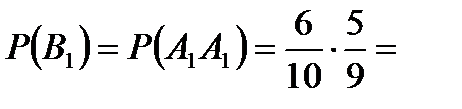 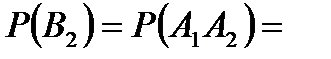 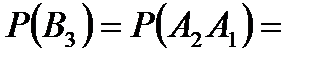 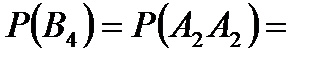 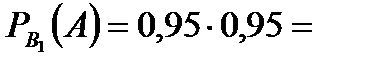 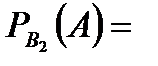 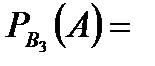 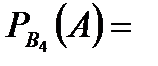 По условию задачи требуется найти вероятность события По условию задачи требуется найти вероятность события 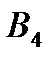 при условии, что произошло событие при условии, что произошло событие 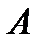 , т.е. , т.е. 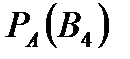 . Применим формулу Байеса: . Применим формулу Байеса: 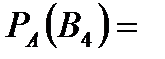 Для этого найдем вероятность события Для этого найдем вероятность события 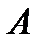 по формуле полной вероятности: по формуле полной вероятности: 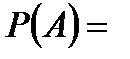 Следовательно, Следовательно, 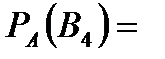 | |||||||||||||||||||||||||||||||
Задача 6.Объект, за которым ведется наблюдение, может быть в одном из двух состояний: 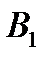 - функционирует, - функционирует, 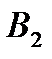 - не функционирует. Априорные вероятности этих состояний: - не функционирует. Априорные вероятности этих состояний: 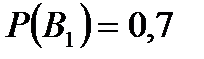 и и 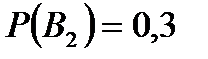 . Имеется два источника информации, которые приносят разноречивые сведения о состоянии объекта: первый источник сообщает, что объект не функционирует, второй, что функционирует. Первый источник дает правильные сведения с вероятностью 0,9, а с вероятностью 0,1, что ошибочные. Второй источник менее надежен: он дает правильные сведения с вероятностью 0,7, а с вероятностью 0,3 – ошибочные. На основе анализа донесений найти новые вероятности гипотез. Решение. Обозначим через . Имеется два источника информации, которые приносят разноречивые сведения о состоянии объекта: первый источник сообщает, что объект не функционирует, второй, что функционирует. Первый источник дает правильные сведения с вероятностью 0,9, а с вероятностью 0,1, что ошибочные. Второй источник менее надежен: он дает правильные сведения с вероятностью 0,7, а с вероятностью 0,3 – ошибочные. На основе анализа донесений найти новые вероятности гипотез. Решение. Обозначим через 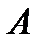 событие, которое произошло, т.е. событие, которое произошло, т.е. 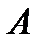 – первый источник сообщил, объект не функционирует ( – первый источник сообщил, объект не функционирует ( 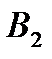 ), второй источник, что функционирует ( ), второй источник, что функционирует ( 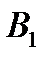 ). Событие ). Событие 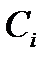 – – 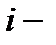 ый источник дает правильные сведения. Событие ый источник дает правильные сведения. Событие 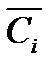 – – 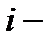 ый источник дает ошибочные сведения. Событие ый источник дает ошибочные сведения. Событие 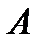 при условии, что объект функционирует, означает, что первый источник дал ошибочные сведения, а второй – верные, т.е. при условии, что объект функционирует, означает, что первый источник дал ошибочные сведения, а второй – верные, т.е. 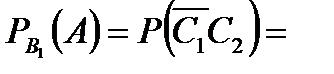 Событие Событие 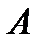 при условии, что объект не функционирует, означает, что первый источник дал верные сведения, а второй – ошибочные, т.е. при условии, что объект не функционирует, означает, что первый источник дал верные сведения, а второй – ошибочные, т.е. 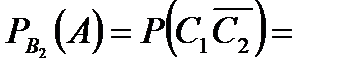 По условию задачи требуется найти вероятности состояний объекта при условии, что произошло событие По условию задачи требуется найти вероятности состояний объекта при условии, что произошло событие 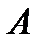 , т.е. , т.е. 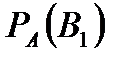 и и 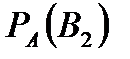 . Для этого найдем вероятность события . Для этого найдем вероятность события 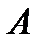 по формуле полной вероятности: по формуле полной вероятности: 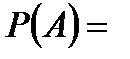 По формуле Байеса По формуле Байеса 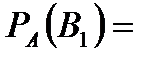 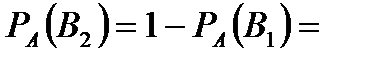 В результате анализа стала значительно более вероятной вторая гипотеза: объект не функционирует. В результате анализа стала значительно более вероятной вторая гипотеза: объект не функционирует. | |||||||||||||||||||||||||||||||
| 4.2. Решить задачу | |||||||||||||||||||||||||||||||
| Задача 7.В составе думы представлены3 партии (по 100, 150, 50 человек от 1-ой, 2-ой и 3-й партий соответственно). Кандидата на должность спикера поддерживают 50% представителей первой партии, 70% - второй партии и 10% - третьей. Какова вероятность того, что наудачу выбранный член думы поддерживает выдвинутую кандидатуру на должность спикера думы? Решение. | |||||||||||||||||||||||||||||||
| Задача 8.Трое рабочих за смену изготовили 60 деталей. Производительность рабочих относится как 1:2:3. Первый рабочий изготавливает в среднем 95% годных деталей, второй 85% и третий 90%. Найти вероятность, того, что наудачу взятая из числа изготовленных за смену деталей низкого качества. Решение. | |||||||||||||||||||||||||||||||
| Задача 9.В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым. Решение. | |||||||||||||||||||||||||||||||
| Задача 10.Турист, заблудившись в лесу, вышел на полянку, от которой в разные стороны ведут 5 дорог. Если он пойдет по первой дороге, то вероятность выхода из леса в течение часа равна 0,6; если по второй – 0,3; если по третьей – 0,2; если по четвертой – 0,1; если по пятой – 0,1. Какова вероятность того, что турист пошел по первой дороге, если через час он вышел из леса? Решение. | |||||||||||||||||||||||||||||||
| Задача 11.Страховая компания разделяет застрахованных потрем классам риска: 1 класс – малый риск, 2 класс – средний, 3 класс – большой риск. Среди всех клиентов компании 50% - первого класса риска, 30% - второго и 20% - третьего. Вероятность наступления страхового случая для первого класса равна 0,01, для второго – 0,03, третьего – 0,08. Какова вероятность того, что клиент, получивший денежное вознаграждение за период страхования, относится к группе малого риска? Решение. | |||||||||||||||||||||||||||||||

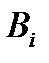 событие, состоящее в том, что при своем движении пешеход попадет в пункт
событие, состоящее в том, что при своем движении пешеход попадет в пункт 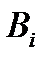 . События
. События 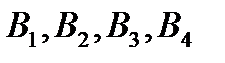 образуют полную группу и очевидно, что они равновероятны (по условию один из путей
образуют полную группу и очевидно, что они равновероятны (по условию один из путей 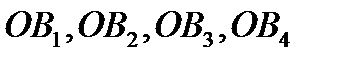 выбирается произвольно). Поэтому
выбирается произвольно). Поэтому 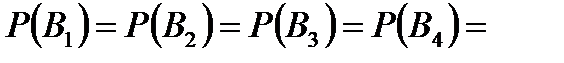
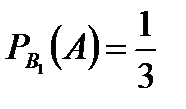 (по классическому определению вероятности).
(по классическому определению вероятности).