Свойства арифметических операций

В классах вычетов

При сравнении по модулю n множество всех целых чисел отображается во множество Z_n = {0, 1, ..., (n - 1)}. При этом возникает вопрос: можно ли определить арифметические операции в рам­ках данного множества? Оказывается, можно, и соответствующий набор опера­ций называется арифметикой в классах вычетов [6,10].

Операции арифметики в классах вычетов обладают следующими свойствами.

1. [(a mod n) + (b mod n)] mod п = (а + b) mod n.

2. [(а mod п) - (b mod n)] mod n = (а - b) mod п.

3. [(а mod п) × (b mod n)] mod n = (а × b) mod n.

Вот несколько примеров, иллюстрирующих указанные три свойства:

19 mod 8=3, 14 mod 8=6;

[(19 mod 8) + (14 mod 8)] mod 8 = 9 mod 8=1;
(19 + 14) mod 8 = 33 mod 8=1;

[(19 mod 8) - (14 mod 8)] mod 8 = - 3 mod 8=5;
(19 - 14) mod 8 = 4 mod 8=4;

[(19 mod 8) × (14 mod 8)] mod 8 = 18 mod 8=2;
(19 × 14) mod 8 = 266 mod 8=2.

Возведение в степень выполняется с помощью повторного умножения, как и в обычной арифметике.

Чтобы найти 11⁷ mod 13, будем действовать следующим образом:

11² = 121 º4 mod 13,

11⁴ º 4² º 3 mod 13,

11⁷ º 11 × 4 × 3 º 132º 2 mod 13.

Итак, правила выполнения обычных арифметических операций — сложения, вычитания и умножения — можно применять и в арифметике классов вычетов.

Для арифметических операций по модулю п в этом множестве выполняются сле­дующие свойства.

Свойство	Выражение
Коммутативный закон	(x + y) mod n = (y + x) mod n (x × y) mod n = (y × x) mod n
Ассоциативный закон	[(x + y) +z)] mod n = [(x + (y + z)] mod n [(x × y) ×z)] mod n = [(x × (y × z)] mod n
Дистрибутивный закон	[(x × y) ×z)] mod n = [(x × y) × (y × z)] mod n
Тождества	(0+ y) mod n = y mod n (1× y) mod n = y mod n
Аддитивный обратный (- y)	Для любого yÎZ существует такое z, что (y + z) mod n ≡ 0 mod n

Существует одна особенность арифметики в классах вычетов, которая делает ее отличной от обычной арифметики. Заметим сначала, что, как и в обычно арифметике, имеет место следующее свойство.

Если (а + b) º (а + с) mod п ,то b º с mod п,(1.8)

(7 + 21) º (7 + 5) mod 8; 21 º 5 mod 8

Свойство (1.7) согласуется с существованием аддитивного обратного. Прибавив к обеим частям равенства (1.7) аддитивное обратное элемента а, получим ((-а) + а + b) = ((-a) + а + с) mod п, b º с mod п.

Однако следующее утверждение выполняется только при указанном ниже условии:

Если (а × b) º (а × с) mod п,то b º с mod п
при условии, что а и п взаимно просты. (1.9)

Рассмотрим пример, когда данное условие не выполнено:

4 × 3 = 12 º 4 mod 8,

4 × 5 = 20 º 4 mod 8.
Однако 3 ¹ 5 mod 8.

Операции над многочленами

Многочленом над полем GF(q) называется математическое выражение:

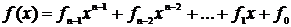, (1.10)

где х - называется фиктивной переменной, коэффициенты f_n-1, f_n-2,…, f₀ принадлежат полю GF(q), а показатели степеней являются целыми числами.

Нулевым многочленом называется многочлен f(x) = 0.

Приведенными многочленами называются многочлены, старший коэффициент которых f_n-1=1. Степенью ненулевого многочлена f(x), которая обозначается deg f(x), называется индекс старшего коэффициента f_n-1.

Множество всех многочленов над полем GF(q) образует кольцо относительно сложения и умножения, определяемых по обычным принципам сложения и умножения многочленов. Такое полиномиальное кольцо можно определить для каждого поля Галуа GF(q). Такое кольцо обозначается GF(q)[x]. Элементы кольца GF(q) называют скалярами.

Суммой двух многочленов f(x)и q(x) из GF(q)[x] называется многочлен из GF(q)[x], определяемый равенством:

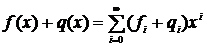. (1.11)

Например, для поля GF(2)

(х⁴ + х ² + х +1)+( х ⁵ + х ⁴ + х ³ +1)=

= х ⁵ +(1Å1) х ⁴ + х ³ + х ² + х +(1Å1)=

= х ⁵ + х ³ + х ² + х.

Произведением двух многочленов из GF(q)[x] называется многочлен, определяемый равенством:

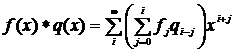. (1.12)

Например, над GF(2)

(х⁴ + х ² +1)×( х ² +1)= х ⁶ +1

Кольцо многочленов во многих отношениях соответствует кольцу целых чисел. Многочлен S(x) делится на многочлен d(x), если существует многочлен a(x), такой, что

d(x)× a(x) = S(x).

Многочлен p(x) делящийся на многочлен a× p(x) или a, называется неприводимым многочленом, где a – произвольный ненулевой элемент поля GF(q). Приведенный неприводимый многочлен называется простым многочленом.

Если S(x) одновременно делится на d(x) и делит d(x), то
S(x) = a× d(x).

Для каждой пары многочленов S(x) и d(x) (при d(x)¹ 0) существует единственная пара многочленов a(x) (частное) и r(x) (остаток), таких, что

S(x) = d(x)× a(x) + r(x), (1.13)

где deg S(x) < deg d(x).

Практическое вычисление частного и остатка осуществляется по обычным правилам деления многочленов. В теории кодирования большое значение имеет остаток. Остаток можно записать в виде:

r(x) = R_d(x)[ S(x)]. (1.14)

Часто остаток называется вычетом многочлена S(x) по модулю многочлена d(x).

r(x) = S(x)[mod d(x)], (1.15)

Несколько отличным понятием является сравнение, которое означает, что при делении на d(x) многочлены S(x)и A(x) дают один и тот же остаток, но deg A(x) необязательно меньше deg d(x).

A(x) ≡ S(x)[mod d(x)], (1.16)

Ненулевой многочлен p(x) над некоторым полем однозначно разлагается в произведение элемента поля и простых многочленов над этим полем.

Наибольший общий делитель двух многочленов S(x) и d(x)
НОД [S(x), d(x)] определяется как приведенный многочлен наибольшей степени, делящий одновременно оба из них. Если НОД [S(x), d(x)] = 1, то они называются взаимно простыми.

Наибольший общий делитель двух многочленов S(x) и d(x) над полем GF(q) можно вычислить с помощью итеративного алгоритма деления Евклида. Если deg S(x) ³ deg d(x) ³ 0, то последовательность вычислений такова:

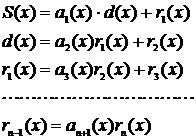. (1.16)

Процесс обрывается, как только будет получен нулевой остаток.

Наибольший общий делитель двух многочленов S(x) и d(x) на основе алгоритма в общем виде (аналогично целым числам) можно записать в виде:

НОД [S(x), d(x)] = a(x)× d(x) + b(x)× S(x), (1.17)

где a(x) и b(x) многочлены над GF(q), которые можно найти из представленной выше системы уравнений (1.16).

Наименьшее общее кратное двух многочленов S(x) и d(x)
НОК[S(x), d(x)] определяется как приведенный многочлен наименьшей степени, делящийся на оба из них. Значение НОК можно вычислить по формуле:

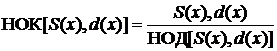. (1.18)

Для произвольного элемента b из GF(q) можно вычислить значение многочлена над GF(q) в этой точке, подставив элемент b вместо x. Например, в поле GF(3), (q={0,1,2})

.

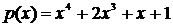Тогда

.

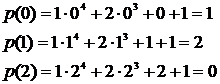Можно вычислить значение многочлена над GF(q) в расширении поля GF(q). Это вычисление проводится подстановкой элементов из расширения поля вместо фиктивной переменной х и выполнением операций в расширении поля. Например, пусть GF(2)

.

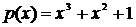Пусть для элементов поля GF(4) имеем следующие правила сложения и умножения:

Таблица 1.3 Таблица 1.4

·

+

Тогда

.

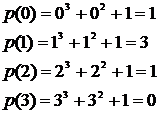Если р(b)=0, то элемент b называется корнем многочлена р(х).

Многочлен необязательно имеет корни в собственном поле. Многочлен 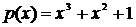не имеет корней в GF(2), но имеет корень в расширении поля, т. е. в GF(4).

Элемент b является корнем многочлена р(х) тогда и только тогда, когда (x-b) делит р(х). У р(х) степени n не более n корней.