Численное интегрирование систем дифференциальных уравнений

Системой дифференциальных уравнений называется система вида

где x - независимый аргумент;

y_i - зависимая функция, ;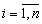

y_i|_x=x0 =y_i0 - начальные условия.

Функции y_i(x), при подстановке которой система уравнений обращается в тождество, называется решением системой дифференциальных уравнений.

Численные методы решения систем дифференциальных уравнений.

1. Метод Эйлера.

y_ij+1=y_ij+hf_i(x_i,y_1j y_2j..y_nj)

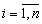
j - номер шага.

x_j+1=x_j+h.

2. Модифицированный метод Эйлера.

k_i1=h*f_i(x_j,y_1j..y_nj)

k_i1=h*f_i(x_j+h,y_1j+k_i1..y_nj+k_i2)

y_ij+1=y_ij+(k_i1+k_i2)/2

x_j+1=x_j+h

3. Метод Рунге-Кутта четвертого порядка.

k_i1=hf_i(x_j,y_1j..y_nj)

k_i2=hf_i(x_j+h/2,y_2j+k_i1/2,..,y_nj+k_n1/2)

k_i3=hf_i(x_j+h/2,y_2j+k_i2/2,..,y_nj+k_n2/2)

k_i4=hf_i(x_j+h,y_1j+k_i2,..,y_nj+k_n3)

y_ij+1=y_ij+(k_i1+2k_i2+2k_i3+k_i4)/6

x_j+1=x_j+h

Дифференциальным уравнением второго порядка называется уравнение вида:

F(x,y,у',y")=0

(1)

или

y"=f(x,y,y').

(2)

Функция y(x), при подстановке которой уравнение обращается в тождество, называется решением дифференциального уравнения.

Численно ищется частное решение уравнения (2), которое удовлетворяет заданным начальным условиям, то есть решается задача Коши.

Для численного решения дифференциальное уравнение второго порядка преобразуется в систему двух дифференциальных уравнений первого порядка и приводится к машинному виду (3). Для этого вводится новая неизвестная функция 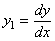, слева в каждом уравнении системы оставляют только первые производные неизвестных функций, а в правых частях производных быть не должно:

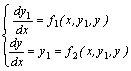(3)

Функция f₂(x, y₁, y) в систему (3) введена формально для того, чтобы методы, которые будут показаны ниже, могли быть использованы для решения произвольной системы дифференциальных уравнений первого порядка. Рассмотрим несколько численных методов решения системы (3). Расчетные зависимости для i+1 шага интегрирования имеют следующий вид. Для решения системы из n уравнений расчетные формулы приведены выше. Для решения системы из двух уравнений расчетные формулы удобно записать без двойных индексов в следующем виде:

1. Метод Эйлера.

у_1,i+1=у_1,i+hf₁(x_i, y_1,i, y_i),

у_i+1=у_i+hf₂(x_i, y_1,i, y_i),

x_i+1=x_i+h.

2. Метод Рунге-Кутта четвертого порядка.

у_1,i+1=у_1,i+(m₁+2m₂+2m₃+m₄)/6,

у_i+1=у_i+(k₁+2k₂+2k₃+k₄)/6,

m₁=hf₁(x_i, y_1,i, y_i),

k₁=hf₂(x_i, y_1,i, y_i),

m₂=hf₁(x_i+h/2, y_1,i+m₁/2, y_i+k₁/2),

k₂=hf₂(x_i+h/2, y_1,i+m₁/2, y_i+k₁/2),

m₃=hf₁(x_i+h/2, y_1,i+m₂/2, y_i+k₂/2),

k₃=hf₂(x_i+h/2, y_1,i+m₂/2, y_i+k₂/2),

m₄=hf₁(x_i+h, y_1,i+m₃, y_i+k₃),

k₄=hf₂(x_i+h, y_1,i+m₃, y_i+k₃),

x_i+1=x_i+h,

где h - шаг интегрирования. Начальные условия при численном интегрировании учитываются на нулевом шаге: i=0, x=x₀, y₁=y₁₀, y=y₀.

Задание для самостоятельной работы

Изучение численных методов решения дифференциальных уравнений второго порядка и систем дифференциальных уравнений первого порядка.

Численно и аналитически найти:

a. закон движения материальной точки на пружине х(t),

b. закон изменения силы тока I(t) в колебательном контуре (RLC - цепи) для заданных в табл.1,2 режимов. Построить графики искомых функций.

Варианты заданий

Таблица режимов:

№	Режим
	Свободные незатухающие колебания
	Затухающее колебательное движение
	Апериодическое движение
	Предельное апериодическое движение
	Вынужденное колебание без сопротивления
	Вынужденное колебание без сопротивления, явление резонанса
	Вынужденное колебание с линейным сопротивлением
	Вынужденное колебание с линейным сопротивлением, явление резонанса

Варианты заданий и номера режимов:

1. движение точк;

2. RLC – цепь.

Вар.	Задание	Вар.	Задание
	а) 1,2,5		б)1,2,6
	а) 1,3,6		а) 1,4,7
	б)1,3,7		б)1,2,7
	а) 1,4,8		а) 1,2,5
	б)1,2,8		б)1,4,6
	а) 1,4,7		а) 1,3,5
	б)1,3,6		б)1,3,8
	а) 1,4,5		б)1,4,5
	б)1,3,8		а) 1,3,6
	а) 1,3,5		б)1,4,7
	б)1,4,6		а) 1,2,8
	а) 1,2,7		б)1,4,8
	б)1,2,5		а) 1,3,6
	а) 1,2,6		б)1,3,7
	б)1,4,7		а) 1,2,5

Рассмотрим более подробно порядок составления дифференциальных уравнений и приведения их к машинному виду для описания движения тела на пружине и RLC-цепи.

a. Движение материальной точки на пружине.

При выполнении этого задания необходимо рассмотреть движение материальной точки массой m на пружине (рис. 14.1) жесткостью c в среде с линейным сопротивлением под действием синусоидальной вынуждающей силы по горизонтальной поверхности.

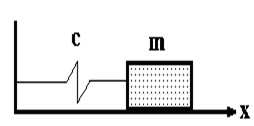
Рис. 14.1 - движение материальной точки на пружине

Уравнение движения (второй закон Ньютона) для материальной точки с учетом действия сил линейного сопротивления (-βx'), упругости пружины (-cx) и синусоидальной силы F₀∙sin(pt) может быть записано следующим образом:

,

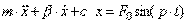где m=1+int(n/2) - масса материальной точки, β - коэффициент сопротивления, с=2+int(n/3) - жесткость пружины, х - координата (х=0 в положении равновесия точки), t - время, p - частота вынужденных колебаний, F₀=n - амплитуда силы, n - номер варианта, int - целая часть числа. Параметры β, p и начальные условия выбираются самостоятельно с учетом рассматриваемого режима.

b. Колебательный контур (RLC цепь) (рис. 14.2):

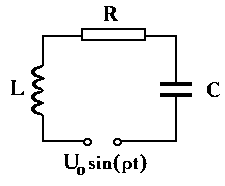
Рис. 14.2. - колебательный контур (RLC цепь)

Уравнение падения напряжения в цепи переменного тока имеет вид

,

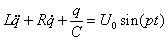где L=1+int(n/2) - индуктивность, R - сопротивление, C=2+int(n/3) - емкость конденсатора, q - заряд, U₀=n-амплитуда напряжения, p - частота, 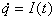- сила тока. Параметры R, p и начальные условия выбираются самостоятельно с учетом рассматриваемого режима.

15 Преобразование Фурье