Компьютерное моделирование. численное интегрирование дифференциальных уравнений
Компьютерные программы, как правило, относящиеся к стандартному программному обеспечению, осуществляют приближенное решение дифференциальных уравнений различными численными методами. Такое решение называют численным интегрированием. Численному интегрированию иногда может предшествовать приближенное, грубое графическое решение для осмысления дальнейших, более точных результатов. Прежде всего, непрерывное уравнение дискретизируется в соответствии с дискретным характером работы компьютера.
При численном интегрировании дифференциального уравнения (в общем случае нелинейного) первого порядка:
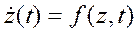
с начальным условием z(t0 ) = z0 выберем фиксированное приращение Δt=h независимой переменной t:
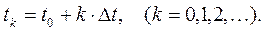
Вычисленные (приближенные) значения решения
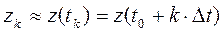
и производной
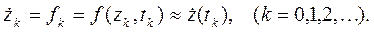
В том случае, если z(t ) представляет собой вектор, а f(z,t) – вектор-функцию правой части дифференциального уравнения, описывающего систему, то модель представляет собой систему уравнений (подобную тем, которые рассмотрены, например, для линейного случая в переменных состояния). Рекуррентные формулы любого из рассматриваемых ниже методов применяются к каждому из уравнений этой системы.
Ошибки усечения и округления
Отвлекаясь от ошибок округления, разность zk+1 – z(tk+1) между вычисленным и точным значением решения называется ошибкой усечения.Если в формуле численного интегрирования заменить точные значения z(tk), z(tk-1),… на zk, zk-1,… , то разность zk+1 – z(tk+1) даст локальную ошибку усечения. Полная ошибка усечения вызывается не только локальной ошибкой, но и распространением ошибок от более ранних шагов интегрирования.
Различают одношаговые и многошаговые методы решения задачи Коши, т.е. нахождения решения рассмотренного выше дифференциального уравнения. К одношаговым методам численного интегрирования относятся методы Эйлера и Рунге–Кутта.
Метод Эйлера
Метод Эйлерасостоит в пошаговом применении простой формулы, которая называется рекуррентной:
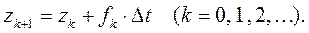 (3.1)
(3.1)
Метод Эйлерадает хорошее приближение решения только при достаточно малом шаге Δt = h и только для нескольких первых точек. Модификации этого метода определяются формулами:
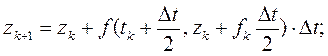 (3.2)
(3.2)
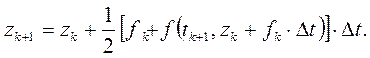 (3.3)
(3.3)
Эти модификации позволяют повысить точность интегрирования за счет «деления шага пополам».
Методы Рунге–Кутта
Методы Рунге–Куттазадаются приведенными ниже рекуррентными формулами. Методы (3.4) и (3.5) называют методами третьего порядка, поскольку формулы для zk+1 являются точными при f(z,t)=1, t, t2, t3; для достаточное количество раз дифференцируемой функции f(z,t) локальная ошибка усечения имеет порядок O(Δt4) при Δt→0. По аналогичным соображениям метод (3.6) называют методом четвертого порядка.
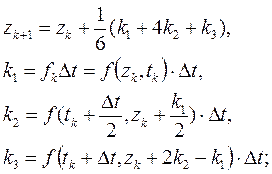 (3.4)
(3.4)
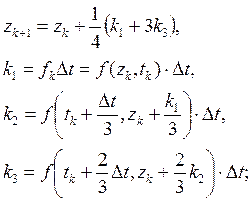 (3.5)
(3.5)
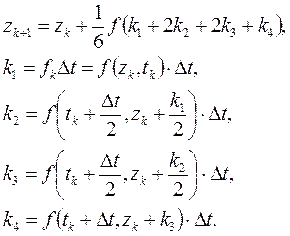 (3.6)
(3.6)
Из этих методов (3.6) является наиболее употребительным.
