Игры без решения в чистых стратегиях

Определение 24. Если платежная матрица игры не имеет седлового элемента, то есть 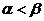, то такую игру называют игрой, не имеющей решения в чистых стратегиях.

В этом случае для каждого игрока важно, чтобы соперник не угадал выбора его стратегии. В этом случае используются смешанные стратегии, при которых реализуется схема случайного выбора чистой стратегии.

Определение 25. Смешанной стратегией первого игрока называют вероятностное распределение на множестве чистых стратегий этого игрока, задаваемого вектором 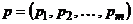, элементы которого удовлетворяют следующим условиям:

1) ( );

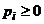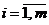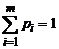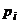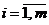2) , где ( ) – вероятности, с которыми первый игрок выбирает свои чистые стратегии .

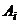Определение 26. Смешанной стратегией второго игрока называют вероятностное распределение на множестве чистых стратегий этого игрока, задаваемого вектором 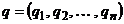, элементы которого удовлетворяют следующим условиям:

1) ( );

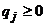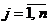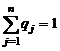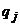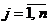2) , где ( ) – вероятности, с которыми второй игрок выбирает свои чистые

стратегии .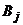

При использовании смешанных стратегий игра приобретает случайный характер. Выбор каждой пары чистых стратегий 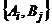является случайным событием и ввиду независимости случайных величин 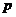и 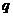реализуется с вероятностью 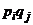. Величина 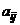выигрыша первого игрока (проигрыша второго игрока) становится случайной функцией смешанных стратеги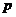й и 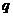и определяется по формуле .

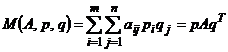Определение 27. Функцию 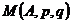называют функцией выигрыша или платежной функцией.

Замечание. Формально функция 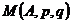представляет собой математическое ожидание выигрыша первого игрока на множестве смешанных стратеги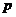й и 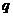. Первый игрок, стремясь достичь наибольшего из гарантированных выигрышей, выбирает вектор вероятностей 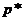так, чтобы получить максимум минимальных значений ожидаемых выигрышей: то есть решает задачу максимина математического ожидания 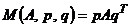: 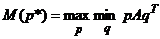. Соответственно, второй игрок решает задачу минимакса математического ожидания 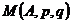– найти такой вектор 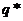, что .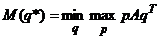

Определение 28. Смешанные стратеги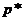и и 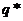называют оптимальными, если они удовлетворяют неравенству .

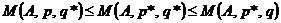Определение 29. Величину 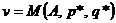называют ценой игры.

Определение 30. Набор 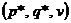, состоящий из оптимальных смешанных стратеги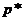й и 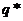и цены игры 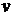, называют решением матричной игры.

Определение 31.Стратегию 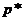первого игрока называют максиминной стратегией, стратегию 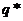второго игрока называют минимаксной стратегией.

Теорема 2 (о минимаксе) (Дж. фон Нейман).Для матричной игры с любой платежной матрицей 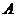справедливы утверждения:

1) величины 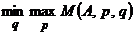, 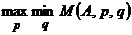существуют и равны между собой: ;

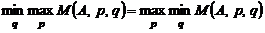2) существует хотя бы одна ситуация в смешанных стратегиях 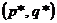, для которой выполняется соотношение

.

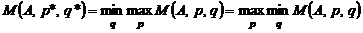Теорема 3 (о свойствах оптимальных стратегий). Пусть 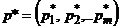, 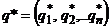– оптимальные смешанные стратегии и 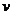– цена игры. Тогда:

1) оптимальная смешанная стратегия 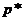первого игрока может быть составлена только из тех чистых стратегий 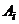( 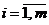), для которых ;

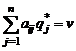2) оптимальная смешанная стратегия 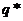второго игрока может быть составлена только из тех чистых стратегий 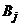( 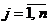), для которых .

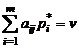Следствие. Имеет место цепочка равенств:

.

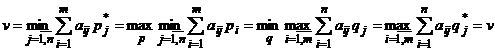Пример 40.5.Найти решение игры, имеющей платежную матрицу

.

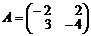Решение.Найдем верхнюю и нижнюю цены игры: 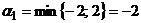, , 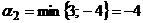нижняя цена игры 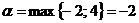; 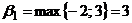, , 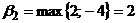верхняя цена игры 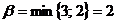. Таким образом, выполняется неравенство 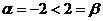, и седловая точка у данной матрицы отсутствует. Задача не имеет решения в чистых стратегиях. Решение игры нужно искать в смешанных стратегиях.

Пусть смешанные стратегии игроков определяются соответственно векторами вероятностей 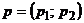, , 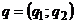для которых 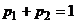, 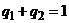– условия нормировки. Функция выигрыша имеет вид

.

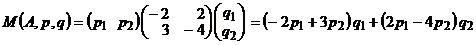Так как первый игрок стремится получить максимальный гарантированный выигрыш 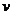, то при оптимальной смешанной стратегии 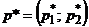должно выполняться равенство 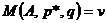или 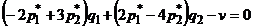. С учетом условий нормировки составим систему уравнений для определения оптимальных стратеги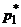й и 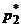первого игрока

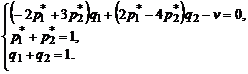
В полученной системе содержится три уравнения и пять неизвестных.

Для отыскания 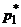и 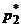воспользуемся следующим приемом исключения неизвестных. Так как 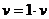и 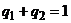, то справедливо равенство 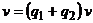. Подставим его в первое уравнение системы:

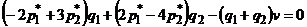
или

.

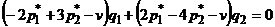В силу теоремы 3 значения 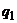и 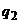являются оптимальными и должны быть отличны от нуля. Следовательно, последнее равенство выполняется при произвольных положительных 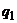и 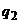только в случае, когда выражения в скобках одновременно равны нулю:

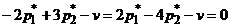или .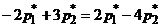

Из условия нормировки 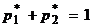выразим 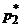и подставим в последнее уравнение: 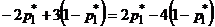. Решая его, получаем 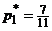, тогда 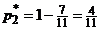. Таким образом, вероятности оптимальных стратегий первого игрока .

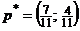Перепишем функцию выигрыша следующим образом:

.

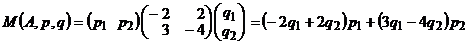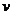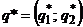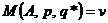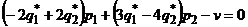Так как второй игрок стремится получить минимальный гарантированный проигрыш , то при оптимальной смешанной стратегии должно выполняться равенство или . С учетом условий нормировки система уравнений для определения оптимальных стратеги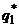й и 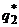второго игрока имеет вид

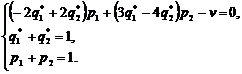
Аналогично для отыскания 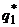и 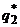из соотношени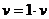й и 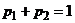имеем право записать 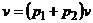. Подставим полученное соотношение в первое уравнение системы, после группировки слагаемых получим уравнение

.

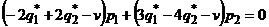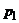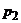Так как по теореме 3 значения и должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных 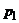и 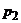только в том случае, когда 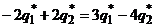. Выразим 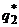из условия нормировки 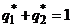, подставим в последнее уравнение и найдем 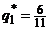, 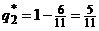. Таким образом, оптимальная смешанная стратегия второго игрока определяется вектором .

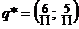Подставим найденные оптимальные вероятности смешанных стратегий в функцию выигрыша, найдем цену игры:

.

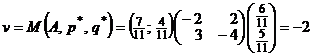Ответ: ; ; .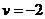

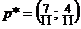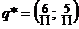Упрощение платежных матриц

Поиск оптимальных стратегий тем сложнее, чем больше размерность платежной матрицы. Поэтому поиск оптимальных стратегий начинают с упрощения платежной матрицы.

Определение 32. Если в платежной матрице элементы 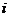-ой строки не меньше соответствующих элементов 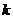-ой строки, то есть 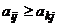( 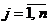), то стратегию 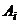называют доминирующей над стратегией 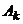(стратегию 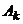называют доминируемой).

Определение 33. Если в платежной матрице элементы 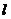-го столбца не больше соответствующих элементов 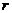-го столбца, то есть 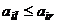( 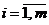), то стратегию 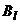называют доминирующей над стратегией 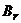(стратегию 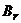называют доминируемой).

Определение 34. Стратег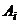ии 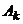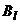и ( и 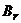) называют дублирующими друг друга, если ( ) ( ( )).

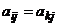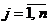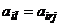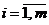Замечание. Дублирование является частным случаем доминирования. Игрокам выгоднее пользоваться доминирующими стратегиями. Поэтому вероятность применения доминируемых стратегий равна нулю. Исключая из платежной матрицы доминируемые стратегии, можно уменьшить ее размерность, что упрощает решение игры. При исключении доминируемых стратегий цена игры не меняется.

Теорема 4. Оптимальные смешанные стратеги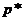и и 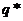в игре с платежной матрицей 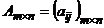и ценой 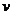остаются оптимальными и для игры с платежной матрицей 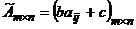( 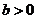) и ценой .

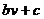На основании теоремы 4 платежную матрицу всегда можно преобразовать так, что ее элементы будут целыми неотрицательными числами, что упрощает расчеты.

Пример 40.6. Найти решение игры, заданной платежной матрицей

.

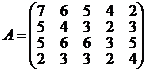Решение. Найдем верхнюю и нижнюю цены игры:

, .

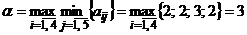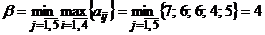Так как 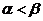, то игра не имеет решения в чистых стратегиях. Оптимальной стратегией первого игрока является стратегия 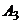, так как в ней расположен максимин 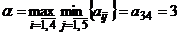. Оптимальной стратегией второго игрока является стратегия 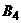, так как в ней расположен минимакс .

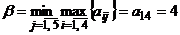Исключим невыгодные стратегии первого игрока. Так как все элементы строки 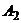не превосходят элементов строки 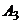, то строку 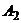можно исключить. Аналогично все элементы строки 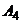не превосходят элементов строки 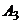, поэтому исключаем 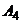. Строку 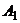исключить нельзя, так как в ней есть элементы, превосходящие элементы строки 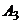. Тогда преобразованная платежная матрица игры будет иметь вид 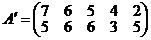. Исключим невыгодные стратегии второго игрока. Все элементы столбцов 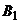, 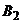и 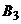больше соответствующих элементов столбца 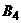, поэтому эти столбцы можно исключить. В столбце 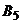есть элементы, меньшие соответствующих элементов столбца 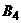, поэтому этот столбец следует оставить. Преобразованная платежная матрица игры будет иметь вид .

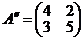Найдем седловую точку матрицы 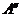в смешанных стратегиях. Пусть смешанные стратегии игроков определяются векторами вероятностей 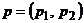, , 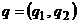компоненты которых удовлетворяют условию нормировки 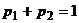, 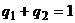. Функция выигрыша будет иметь вид

.

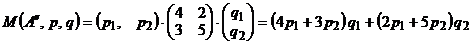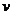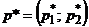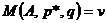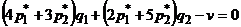Так как первый игрок стремится получить максимальный гарантированный выигрыш , то при оптимальной смешанной стратегии должно выполняться равенство или . С учетом условий нормировки система уравнений для определения оптимальных стратеги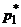й и 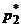первого игрока имеет вид

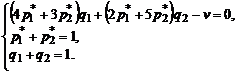
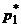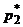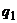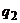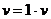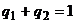В ней содержится 3 уравнения и 5 неизвестных. Для отыскания и исключим переменные и с помощью подстановки: так как и , то 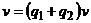. Тогда первое уравнение системы после подстановки в него выражения 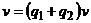и группировки слагаемых относительно 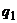и 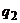можно записать следующим образом: .

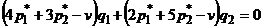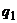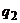Так как по теореме 3 значения и должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных 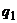и 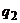только в том случае, когда выполняется равенство 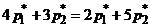. Из условия нормировки 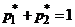выразим 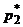и подставим в полученное равенство. Раскрывая скобки и выражая 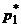, получим 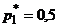, 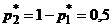. Таким образом, вероятности стратегий первого игрока , .

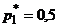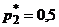Применяя аналогичный прием для отыскания 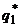и 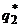получаем, что вероятности стратегий второго игрока , .

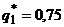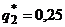Подставим найденные оптимальные смешанные стратегии в функцию выигрыша, найдем цену игры .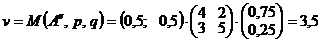

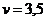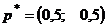Ответ. Цена игры при и 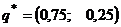. Первый игрок может с одинаковыми вероятностями применять обе стратегии. Второму игроку выгоднее чаще использовать первую стратегию.

40.5. Графический метод решения матричных игр,
не имеющих решения в чистых стратегиях

Для построения решений игр, в которых число стратегий хотя бы одного из игроков равно двум, существует достаточно эффективный графический метод. Будем предполагать, что в рассматриваемых играх нет седловой точки в чистых стратегиях.

Определение 35. Матричную игру, в которой число стратегий первого игрока равно двум, а число стратегий второго игрока равно 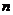, называют 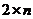-игрой.

Платежная матрица первого игрока 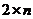-игры имеет вид

.

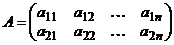Определение 36. Ломаную линию, состоящую из отрезков семейства прямых 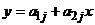( 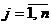) и расположенную не выше каждой прямой семейства, называют нижней огибающей семейства прямых ( ).

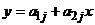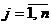Определение 37. Ломаную линию, состоящую из отрезков семейства прямых 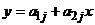( 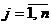) и расположенную не ниже каждой прямой семейства, называют верхней огибающей семейства прямых ( ).

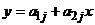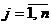Замечание. Нижнюю и верхнюю огибающие семейства прямых будем обозначать соответственно , .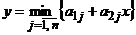

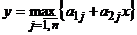Определение 38. Матричную игру, в которой число стратегий первого игрока равно 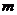, а число стратегий второго игрока равно двум, называют 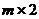-игрой.

Платежная матрица 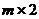-игры имеет вид .

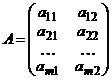Определение 39. Матричную игру, заданную платежной матрицей размерности 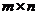называют 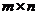-игрой.

Замечание. Если матричную 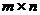игру можно свести к игре 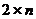или 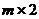, то ее всегда можно решить графическим методом.

Обозначим 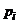– вероятность применения первым игроком стратегии 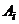, 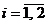; 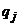– вероятность применения вторым игроком стратегии , , , .

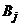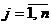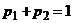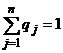Алгоритм графического решения 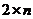-игры

1) Проверить, что игра не имеет решения в чистых стратегиях.

2) Исключить невыгодные стратегии второго игрока, упростить платежную матрицу.

3) На отрезке 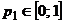построить семейство прямых 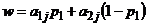( 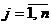), уравнения которых составлены с использованием столбцов упрощенной платежной матрицы 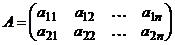и условия нормировки .

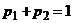4) Построить нижнюю огибающую 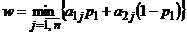, выделить ее высшую точку 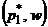и стратегии второго игрока, прямые которых проходят через точку .

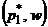5) Найти оптимальные стратегии игроков. В зависимости от формы нижней огибающей может представиться несколько случаев.

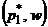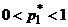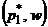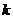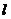Первый случай. Нижняя огибающая имеет ровно одну наивысшую точку , , в точке пересекаются ровно две прямые (например, с номерами и ), соответствующие чистым стратегиям 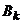и 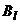второго игрока (рис. 40.1, а)). Для отыскания оптимальной смешанной стратегии первого игрока необходимо выполнить следующие действия:

а) найти координаты точки 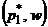как решение системы уравнений, соответствующих чистым стратегиям 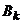и 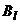второго игрока:

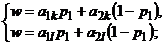
б) найти оптимальную смешанную стратегию первого игрока 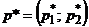, в которой .

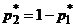Для отыскания оптимальной смешанной стратегии второго игрока необходимо выполнить следующие действия:

а) в платежной матрице оставить только столбцы, соответствующие стратегиям 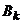и 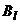второго игрока: ;

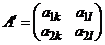б) с использованием строк матрицы 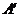составить систему уравнений

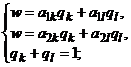
в) найти решение 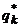и 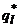полученной системы уравнений;

г) составить оптимальную смешанную стратегию второго игрока, полагая вероятности исключенных стратегий второго игрока равными нулю: .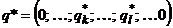

Второй случай. Нижняя огибающая имеет ровно одну наивысшую точку 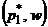, , 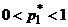в точке 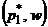пересекается более двух прямых, соответствующих чистым стратегиям второго игрока. Для отыскания оптимальной смешанной стратегии следует выбрать прямые, входящие в нижнюю огибающую (рис. 40.1, б)), а затем провести вычисления, аналогичные первому случаю.

Третий случай. Нижняя огибающая имеет ровно одну наивысшую точку 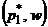, 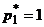. Тогда оптимальной стратегией первого игрока является чистая стратегия 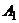, 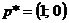. В качестве оптимальной стратегии второго игрока следует выбрать чистую стратегию 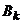, соответствующую прямой с наименьшимположительным наклоном, проходящей через точку 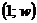(рис. 40.1, в)). Далее следует составить оптимальную смешанную стратегию второго игрока, полагая 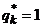, а вероятности остальных стратегий – равными нулю.

Четвертый случай. Нижняя огибающая имеет ровно одну наивысшую точку 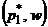и 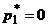. Тогда оптимальной стратегией первого игрока является чистая стратегия 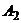, 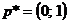. В качестве оптимальной стратегии второго игрока следует выбрать чистую стратегию 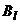, соответствующую прямой с наибольшимотрицательным наклоном, проходящей через точку 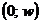(рис. 40.1, г)). Далее следует составить оптимальную смешанную стратегию второго игрока, полагая 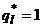, а остальные вероятности равными нулю.

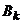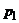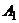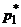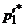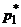Пятый случай. Нижняя огибающая имеет горизонтальный участок, соответствующий чистой стратегии второго игрока (рис. 40.1, д)). Тогда первый игрок имеет бесконечно много оптимальных смешанных стратегий. Вероятность применения первым игроком стратегии может изменяться от до ( и 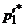– абсциссы точек пересечения прямой, соответствующей чистой стратегии 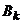, с другими прямыми, образующими нижнюю огибающую). Вероятность 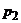применения первым игроком стратегии 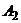может изменяться от 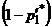до 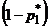. Оптимальной стратегией второго игрока является чистая стратегия 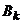, , 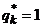вероятности остальных стратегий равны нулю.

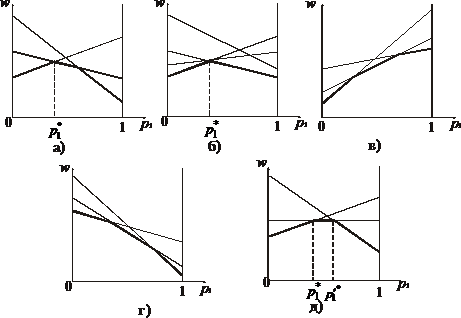
Рис. 40.1

6) Найти цену игры 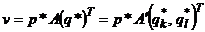. Записать ответ.

Замечание.Выражение 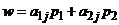характеризует ожидаемый средний выигрыш первого игрока при применении вторым игроком чистой стратегии ( ).

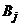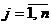Графическое решение 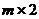-игры во многом аналогично графическому решению 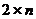-игры, но проходит в другой последовательности.

Алгоритм графического решения 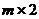-игры

1) Проверить, что игра не имеет решения в чистых стратегиях.

2) Исключить невыгодные стратегии первого игрока, упростить платежную матрицу.

3) На отрезке 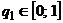построить семейство прямых 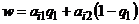( 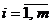), уравнения которых составлены с использованием строк упрощенной платежной матрицы и условия нормировки .

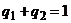4) Построить верхнюю огибающую 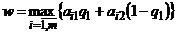, выделить ее низшую точку 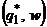и стратегии второго игрока, прямые которых проходят через точку .

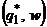5) В платежной матрице оставить только строки, соответствующие стратегиям 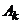и 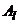первого игрока: .

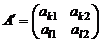6) Найти оптимальные стратегии игроков с использованием верхней огибающей. В зависимости от формы верхней огибающей также может представиться несколько случаев, вычисления в которых проводят аналогично.

7) Найти цену игры по формуле теоремы 3: 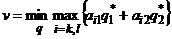. Записать ответ.

Пример 40.7. Найти решение 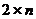-игры, заданной платежной матрицей

.

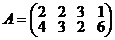Решение. 1) Найдем верхнюю и нижнюю цены игры:

, .

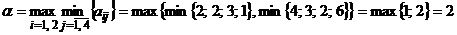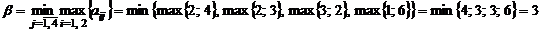Так как 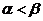, то решения игры в чистых стратегиях нет.

Обозначим 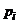– вероятность применения первым игроком стратегии 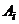, 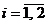; 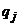– вероятность применения вторым игроком стратегии 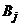, 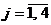. Условия нормировки: , .

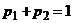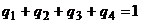2) Упростим платежную матрицу. Заметим, что элементы первого столбца не меньше соответствующих элементов второго столбца. Следовательно, стратегия 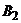является доминирующей над стратегией 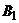. Других доминирующих стратегий в матрице 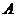нет. Исключим стратегию 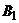, тогда 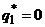. Матрица 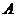примет вид .

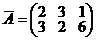3) По столбцам платежной матрицы 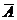с учетом условия нормировки 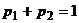составим уравнения семейства прямых 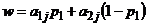( 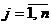), соответствующих чистым стратегиям второго игрока.

Стратегии второго игрока	Ожидаемый средний выигрыш первого игрока	Уравнение прямой

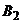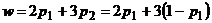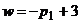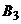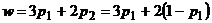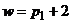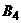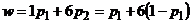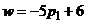Построим полученные прямые на отрезке 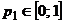(рис. 40.2).

4) Выделим нижнюю огибающую. Из рис. 40.2 видно, что наивысшая точка нижней огибающей лежит внутри интервала 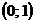и является точкой пересечения прямых 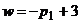и 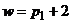, которые соответствуют стратегиям 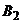и 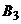второго игрока.

5) Так как нижняя огибающая имеет одну наивысшую точку внутри интервала 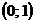, через которую проходят ровно две прямые, соответствующие стратегиям 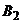и 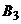, то имеет место первый случай. Найдем оптимальную смешанную стратегию первого игрока:

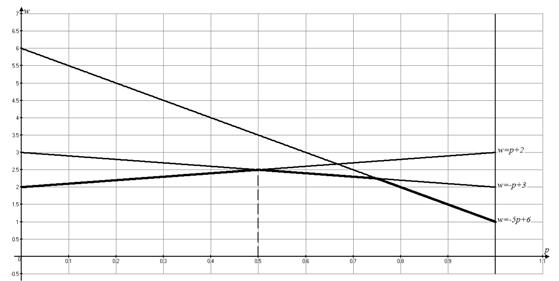
Рис. 40.2

а) найдем точку пересечения прямых 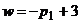и :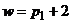

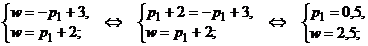
таким образом, ;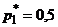

б) вычислим 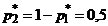, следовательно