Матричные игры двух лиц с нулевой суммой, разрешимость в чистых и смешанных стратегиях.

Отвлечёмся теперь от задач оптимизации, которые как в жизни, так и в нашем пособии занимают, вероятно, ведущее место; и рассмотрим некоторые другие математические модели экономических явлений. В настоящем разделе мы обратимся к моделированию конфликтных ситуаций (т.е. взаимоотношений нескольких субъектов с противоположными экономическими интересами) с помощью математической теории игр. Для простоты рассмотрения будем предполагать, что в конфликте участвуют только два субъекта, называемых игроками. Исход конфликта для каждого из них будем называть выигрышем данного игрока; при этом, чтобы не вводить отдельно понятия проигрыша, условимся фиксировать проигрыш, скажем, тысячи рублей как выигрыш равный (−1000 рублей). Мы ещё более ограничим класс рассматриваемых игр, предполагая, что выигрыш одного игрока всегда равен проигрышу другого; иными словами, сумма их выигрышей равна нулю. Такую игру естественно назвать игрой с нулевой суммой. Мы предполагаем, что у нашей игры есть чёткие правила, т.е. система условий, определяющая варианты действий игроков, объём информации каждого игрока о поведении другого и величину выигрыша игрока в зависимости от его действий. Выбор и осуществление одного из разрешённых правилами действий называется ходом игрока. Наконец, стратегией игрока назовём выбранный им алгоритм, определяющий его ходы в зависимости от текущей игровой ситуации. Мы будем рассматривать лишь конечные игры, в которых у каждого игрока имеется лишь конечное число возможных игровых стратегий. Такие игры также называются матричными.

Целью математической теории игр является определение оптимальной стратегии для каждого из игроков. Какая стратегия игрока называется оптимальной? Такая, которая позволяет ему получать максимальный выигрыш при условии, что второй игрок придерживается своей стратегии. Важное условие состоит здесь в том, что пара оптимальный стратегий (для обоих игроков) должна обладать свойством устойчивости, т.е. каждому из них должно быть невыгодно отклоняться от своей оптимальной стратегии при условии, что второй игрок продолжает придерживаться своей оптимальной стратегии. Если игра повторяется много раз, то естественно рассматривать не выигрыш в каждой отдельной игре, а средний выигрыш за всю серию игр. Негласным предположением в нашей теории является предположение о том, что игроки действуют строго и жёстко в своих интересах.

Итак, наша задача – найти, если возможно, устойчивую пару оптимальных стратегий для игроков; иными словами, найти решение игры или решить игру.

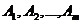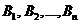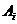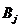Рассмотрим более подробно конечную игру двух игроков с нулевой суммой. Назовём игроков A и B; и пусть все возможные стратегии игрока A – это , а все стратегии B – . Выбор игроками пары стратегий и однозначно определяет выигрыш 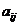игрока A, и выигрыш 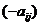игрока B (наша игра – с нулевой суммой). Матрица 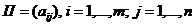называется платёжной матрицей. Рассмотрим конкретный пример.

Пусть наши игроки A и B играют в такую игру: каждый из них выбирает независимо от другого (не зная о выборе другого) одно из чисел 1, 2 или 3. При этом, если произведение выбранных ими чисел чётно, то такое количество рублей B платит A; а если оно нечетно, то наоборот, столько рублей A заплатит B. Составляем платёжную матрицу :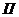

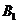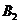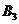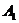	−1		−3
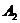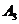	−3		−9

(11.1)

(Имеется в виду, что стратегия 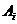означает выбор игроком A числа 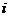и аналогично для B). Займёмся теперь выбором оптимальных стратегий. Сначала будем планировать игру «за» игрока A. Перед нами «былинный» выбор трёх путей 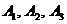. Посмотрим теперь, что же нас (т.е. игрока A) ожидает на каждом из них. Если мы выбираем стратегию 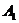, то в самом худшем случае наш выигрыш будет равен 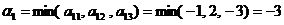. (Т.е. мы проиграем 3 рубля!) Аналогично, если мы выберем «дорогу» 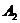, то в худшем случае наш выигрыш будет равняться 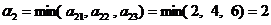(рубля).

И, наконец, в случае выбора стратегии 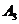нам «грозит» выигрыш 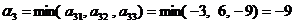, т.е. проигрыш девяти рублей. Какой из «путей» выбрать? Не рассчитывая на везение, мы выберем такую стратегию, при которой самый худший сценарий будет относительно лучшим; иными словами, выбираем стратегию с наибольшим числом 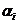: в нашем примере, стратегию 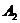. Число 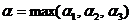называют нижней ценой игры. В нашем примере 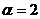. Легко видеть, что когда мы выбираем именно стратегию 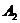, мы всегда будем выигрывать не менее этой суммы; а поскольку этот выбор стратегии в руках игрока A, то 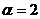является гарантированным выигрышем игрока A при любой стратегии игрока B. В силу предыдущего, он вычисляется по формуле

.

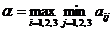Поэтому стратегию игрока A, обеспечивающую этот гарантированный выигрыш ( 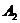в нашем примере), принято называть максиминной.

Будем теперь «болеть» за игрока B. Перед ним также лежит развилка трёх «дорог»: 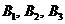. Какую же выбрать? Посмотрим, что самое худшее может случиться с игроком B на «дороге» 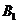: рассматривая первый столбец в платёжной матрице (11.1) и вспоминая, что числа в клетках представляют собой проигрыши игрока B, мы видим, что наихудшим является проигрыш 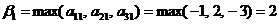(двух рублей). Аналогично, в случае выбора игроком B стратегий 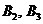самыми худшими вариантами будут проигрыши соответственно 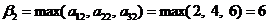и

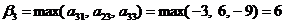(шести рублей).

Отсюда мы (т.е. игрок B) видим, что если везение от нас отвернётся, то проигрыш неизбежен; но, по крайней мере, мы можем его минимизировать, выбирая стратегию с наименьшим наихудшим проигрышем 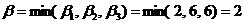. Или в терминах элементов платёжной матрицы

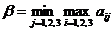
Поэтому соответствующая стратегия игрока B (стратегия 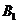в примере) называется минимаксной стратегией. Число 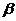носит название верхней цены игры. Такое название связано с тем фактом, что всегда мы имеем неравенство 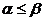. Действительно, для каждого 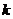мы имеем 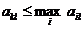. Отсюда 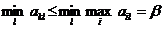. Следовательно, 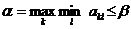, что и требовалось получить.

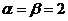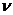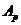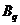В нашем примере мы, однако, имеем даже равенство . В этом случае это общее значение нижней и верхней цены игры называют просто ценой игры . Пусть в этом случае и − максиминная и минимаксная стратегии. Тогда, в силу способов построения нижней и верхней цены игры, мы имеем 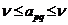(продумайте этот момент самостоятельно). И, значит, 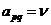. Таким образом, число 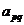является наименьшим в своей строке и наибольшим в своём столбце. Мы имеем так называемую седловую клетку в таблице. А отсюда ясно, что в этом случае пара стратегий – максиминная и минимаксная – является устойчивой парой: ни одному из игроков невыгодно первому уходить от своей стратегии! Таким образом, если 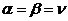мы имеем решение нашей игры в чистых стратегиях.

Наоборот, если имеется решение в чистых стратегиях, т.е. устойчивая пара стратеги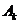й и 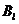; то в силу устойчивости клетка 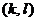в таблице является седловой, и тогда мы имеем 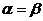(убедитесь в этом).

Вывод:матричная игра с нулевой суммой имеет решение в чистых стратегиях тогда и только тогда, когда выполняется равенство .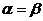

В рассмотренном примере игры выполнялось соотношение 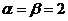, и решение игры доставляла пара стратегий 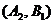. Таким образом, теория игр рекомендует игроку A выбирать число 2, а игроку B – число 1.

Раздел 12