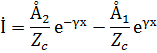Установившийся режим в однородной линии с РП при синусоидальном напряжении источника питания.

Установившийся режим в однородной линии с РП при синусоидальном напряжении источника питания.

Запишем уравнение (1) для установившегося режима, вводя комплексные напряжения, токи, сопротивления и проводимости и переходя от частных производных к полным.

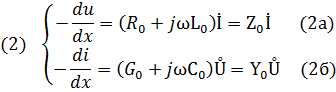
ГдеZ₀= R₀+jωL₀ – комплексное продольное сопротивление линии единичной длины

Y₀= G ₀+jωC₀ - комплексная проводимость линии единичной длины (Z₀≠(1/Y₀))

Решим уравнение (2а) относительно Ů для чего продифференцируем его по х и вместо 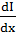возьмем его выражение из (2б)

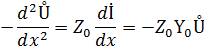
Получение уравнения представляет собой линейное дифференциальное уравнение 2-го порядка , решением которого является

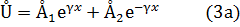
Где Å₁ и Å₂ – постоянные интегрирования, комплексные числа, которые могут быть выражены через напряжение и ток в начале или в конце линии .

ᵞ- постоянная распространения, комплексное число , которое обычно представляют так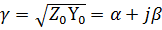

Где α- коэффициент затухания, характеризует затухание падающей волны на единицу длины линии [Нп/км]

β-коэффициент фазы, характеризует изменение фазы падающей волны на единицу длины линии[рад/км]/

Так в линии можно определить из уравнения (2а)

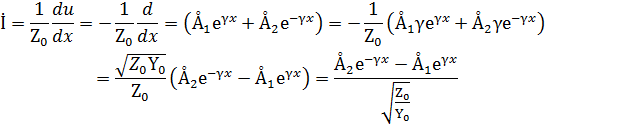
Отношение 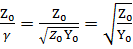имеющее размерность сопротивления обозначают Z_ви называют волновым сопротивлением. Для однородной линии, рассматриваемой между ее входными и выходными выводами как четырехполюсник, волновое сопротивление совпадает с характеристическим Z_с .

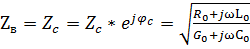–это комплексное характеристическое сопротивление линии с РП.

Окончательно запишем для тока

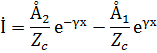
Первичные и вторичные параметры однородной линии с РП.

К первичным параметрам линии с РП относят удельные : активное сопротивление R₀, индуктивность L₀, активную проводимость G₀, удельную емкость С₀.

К ним также относят удельное продольное сопротивления Z₀=R₀+jωL₀и удельную проводимость Y₀=G₀+jωC₀

Но вторичным параметрам или волновым постоянным линий с РП относятся

1) Коэффициент распространения ϒ

ϒ=α+jβ

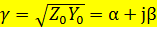
2) Волновое сопротивление Z_в=[Ом]

Вторичные параметры ϒ и Z_в зависят от частоты, поэтому работа линии с РП в режиме согласованной нагрузки возможно только на одной фиксированной частоте.

Коэффициент отражения волны .

,отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии называется коэффициентом отражения волны по напряжению K_u.

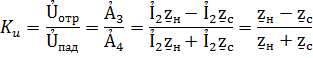
Коэффициент отражения зависит от соотношения между сопротивлением нагрузки и волновым сопротивлением

При к.з. ,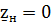

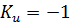
При х.х. ,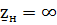

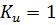
При ,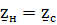

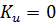
Наряду с коэффициентом отражения по напряжению говорят также и о коэффициенте отражения по току .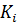

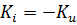
Линии с РП без искажений .

Для любой линии с РП при ее практическом использовании для передачи электрического сигнала в системе связи или телевещания решающее значение имеет ее способность передавать соответствующий электрический сигнал без искажения его формы.

Неискаженной передачей сигнала называется такая передача, при которой форма сигнала в начале и в конце линии одинакова, т.е все ординаты кривых тока и напряжения в конце линии прямо пропорциональны соответствующим ординатам кривых Ủи Ỉ в начале линии.

Достигнуть этого можно в том случае, если коэффициент затухания α и фазовая скорость 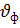не зависят от частоты сигнала, а коэффициент фазы β пропорционален частоте, т.е.

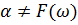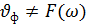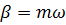; ; гдеm=const.

Хэвисайд доказал, что неискажающая передача сигнала возможна, когда соблюдается условие неискажения 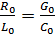и действительно, если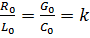

То 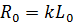; 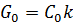в результате

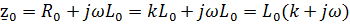
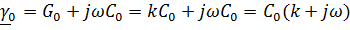
Поэтому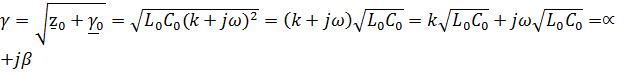

Откуда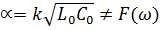

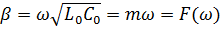
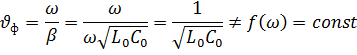
Итак, линию, параметры которой удовлетворяют условию Хэвисайда и вдоль которой волны всех частот распространяютсяс одинаковой скоростью 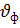и затухают в равной степени называют линией без искажений.

Волновое сопротивление линии без искажений равно

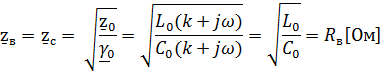
Т.е. волновое сопротивление линии без искажений имеет чисто активный характер, а значит при согласованной нагрузке в любой точке линии Ủи Ỉ совпадают по фазе.

Если учесть при этом, что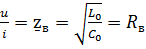

То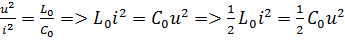

Где 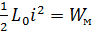- энергия магнитного поля

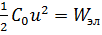-энергия электрического поля

Т.е для любого участка линии без искажения при согласованной нагрузке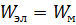

В реальных линиях 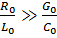. При этом в линиях возникают искажения двух типов:

1)амплитудные- при которых амплитуда сигналов разных частот затухают неодинаково

2)фазовые- при которых 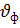различна для разных частот.

Чтобы реальная линия отвечала условию Хэвисайда необходимо либо уменьшить 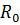или 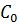, либо увеличить 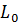или 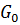. На практике применяют именно увеличение 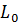путем включения в линию через участки небольшой длинны катушки индуктивности. Этим способом удается обеспечить приемственность неискаженного сигнала при длине линии о 2,5 тыс.км. однако при этом уеличивается время прохождения сигнала.

Линия без потерь.

Независимо от того соблюдается или нет условие Хэвисайда всегда желательно, чтобы активное сопротивление линии 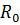и проводимость изоляции 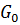были как можно меньше, т.к. при этом уменьшаются потери энергии в линии

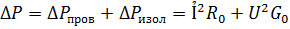
В реальных воздушных линиях, обычно, 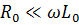и 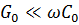. Поэтому в ряде случаев оказывается возможным принебречь активным сопротивление 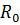и проводимостью изоляции .

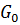Линии в которых 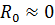и 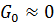называются линиями без потерь или идеальными линиями.

В линии без потерь имеем:

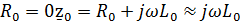
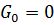
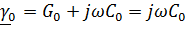
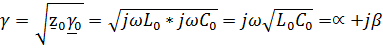
Откуда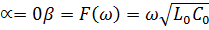

Фазовая скорость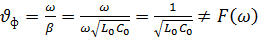

Т.е. всякая линия без потерь является неискаженной линией.

Волновое сопротивление линии без потерь

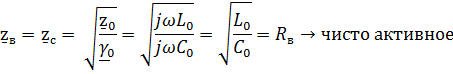
Уравнение линии без потерь можно представить в след виде

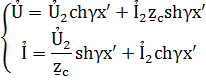
Т.к. линия идеальная то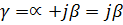

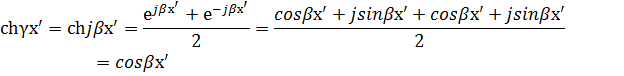
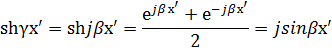
после подстановки получим

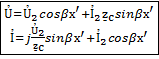- уравнение линии без потерь.

Установившийся режим в однородной линии с РП при синусоидальном напряжении источника питания.

Запишем уравнение (1) для установившегося режима, вводя комплексные напряжения, токи, сопротивления и проводимости и переходя от частных производных к полным.

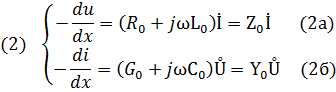
ГдеZ₀= R₀+jωL₀ – комплексное продольное сопротивление линии единичной длины

Y₀= G ₀+jωC₀ - комплексная проводимость линии единичной длины (Z₀≠(1/Y₀))

Решим уравнение (2а) относительно Ů для чего продифференцируем его по х и вместо 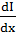возьмем его выражение из (2б)

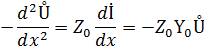
Получение уравнения представляет собой линейное дифференциальное уравнение 2-го порядка , решением которого является

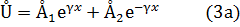
Где Å₁ и Å₂ – постоянные интегрирования, комплексные числа, которые могут быть выражены через напряжение и ток в начале или в конце линии .

ᵞ- постоянная распространения, комплексное число , которое обычно представляют так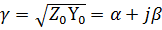

Где α- коэффициент затухания, характеризует затухание падающей волны на единицу длины линии [Нп/км]

β-коэффициент фазы, характеризует изменение фазы падающей волны на единицу длины линии[рад/км]/

Так в линии можно определить из уравнения (2а)

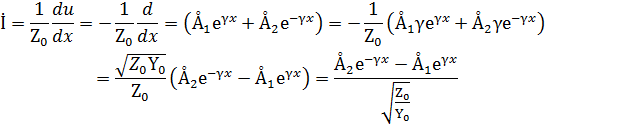
Отношение 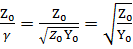имеющее размерность сопротивления обозначают Z_ви называют волновым сопротивлением. Для однородной линии, рассматриваемой между ее входными и выходными выводами как четырехполюсник, волновое сопротивление совпадает с характеристическим Z_с .

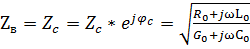–это комплексное характеристическое сопротивление линии с РП.

Окончательно запишем для тока