Выборка из двумерной генеральной совокупности

Системой случайных величин (СВ) называют совокупность СВ, характеризующих состояние рассматриваемой системы или исход данного опыта.

Обозначение:

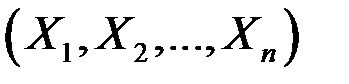– n-мерная СВ.

Каждую из величин 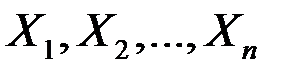называют составляющей или компонентой.

Различают дискретные и непрерывные многомерные СВ: дискретные – если составляющие этих величин дискретны, и непрерывные – когда составляющие этих величин непрерывны.

Полной характеристикой ССВ является ее закон распределения, который может иметь разные формы: функция распределения, плотность распределения, таблица вероятностей отдельных значений случайного вектора и т.д.

Рассмотримдвумерную СВ 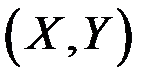, возможные значения которой – пары чисел .

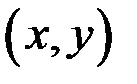Закон распределения дискретной двумерной СВ 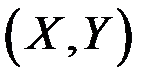может бытьзадан таблицей распределения (матрицей распределения) (таблица 3), элемент которой, стоящий на пересечении i-той строки и j-того столбца, равен вероятности того, что двумерная случайная величина 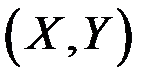имеет значение :

.

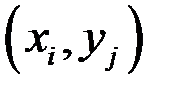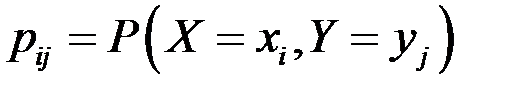Таблица 3

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

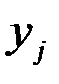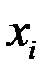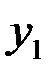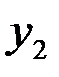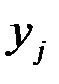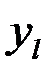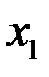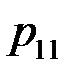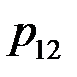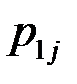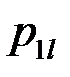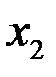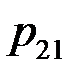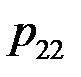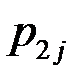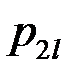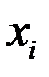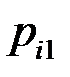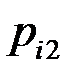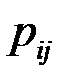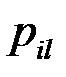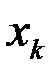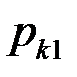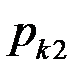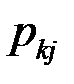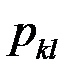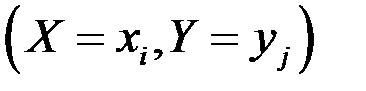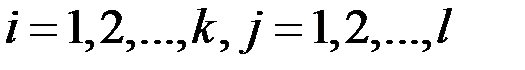События при образуют полную группу, поэтому сумма всех вероятностей 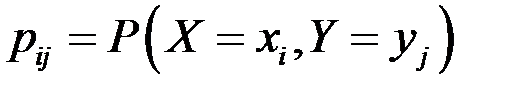равна единице:

.

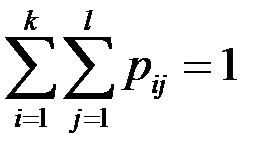Зная матрицу распределения двумерной ДСВ можно найти законы распределения каждой из составляющих. Чтобы найти вероятность того, что одномерная случайная величина Х илиY примет значение 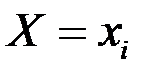или 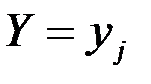, следует сложить все вероятности 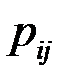, стоящие в строке с номером iили столбце с номером j.

Две случайные величины Х и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое возможное значение приняла другая случайная величина. В противном случае величины Х и Y называются зависимыми.

При изучении двумерных случайных величин рассматриваются числовые характеристики одномерных составляющих Х и Y - математические ожидания и дисперсии: 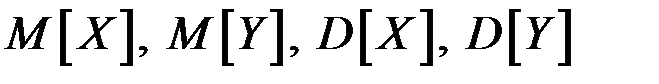. Также рассматриваются условные математические ожидания и условные дисперсии. Например, условным математическим ожиданием одной из случайных величин, входящих в систему 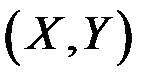, называется ее математическое ожидание, вычисленное при условии, что другая случайная величина приняла определенное значение.

Условное математическое ожидание случайнойвеличиныY при заданном 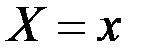, т.е. функция

,

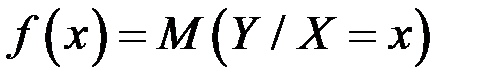называется функцией регрессиислучайной величиныY относительно случайной величиныХ (у на х). График этой функции называется линией регрессии у на х.

Аналогично определяется функция регрессии х на у,

Числовые характеристики системы не исчерпываются числовыми характеристиками случайных величин, входящих в систему. Может иметь место взаимная связь между случайными величинами, составляющими систему. Для ее описания вводят в рассмотрение числовую характеристику – корреляционный момент.

Корреляционным моментом(или ковариацией) 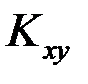случайных величин Х и Yназывается математическое ожидание произведения отклонения этих величин от своих математических ожиданий:

.

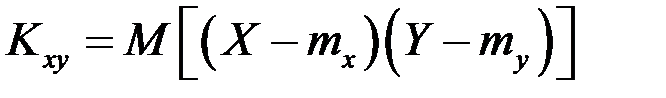Эта характеристика помимо рассеяния величин Х и Y описывает еще и связь между ними. Если случайные величиныХ и Y независимы друг от друга, то корреляционный момент 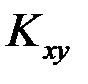равен нулю. Обратное утверждение неверно, т.е. из равенства нулю корреляционного момента 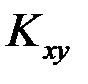не следует независимость случайных величин Х и Y.

Формула для вычисления корреляционного момента дискретных случайных величин:

.

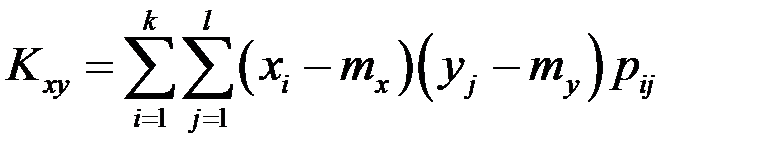Для характеристики связи между величинами Х и Y в чистом виде переходят от момента 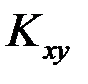к безразмерной характеристике -коэффициенту корреляциислучайных величин Х и Y:

,

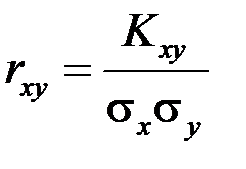где 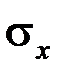и 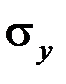– средние квадратические отклонения величин Х и Y.

Коэффициент корреляции принимает значения на отрезке :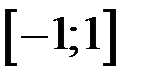

.

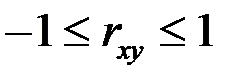Если случайные величины Х и Yнезависимы, то их коэффициент корреляции равен нулю.

Случайные величины, для которых корреляционный момент, а значит и коэффициент корреляции, равен нулю, называется некоррелированными(несвязанными).

Две независимые случайные величины всегда являются некоррелированными. Обратное утверждение не всегда верно, могут быть случаи, когда случайные величины являются некоррелированными, но зависимыми.

Если 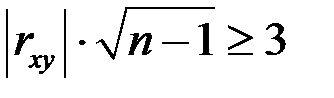, где n – число двумерных случайных величин, то связь между случайными величинами Х и Y достаточно вероятна.

Рассмотрим выборку из двумерной генеральной совокупности, отождествляемой с системой двух случайных величин 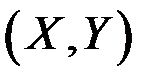. В результате n независимых наблюдений получили n пар чисел:

.

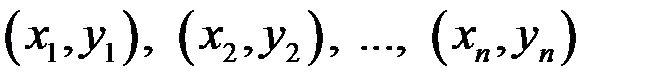Статистический материал сводят в корреляционную таблицу (таблица 4):

Таблица 4

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…
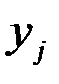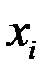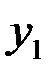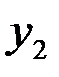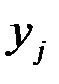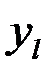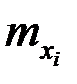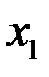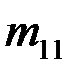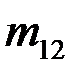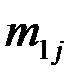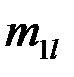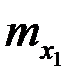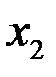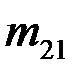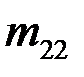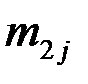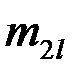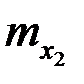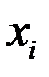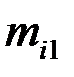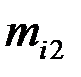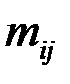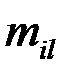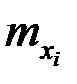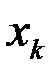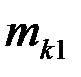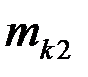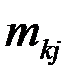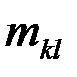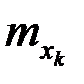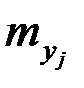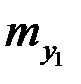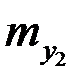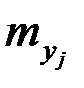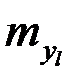							n

где 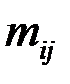- частоты наблюденных пар значений признаков 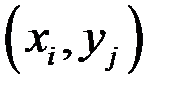, , 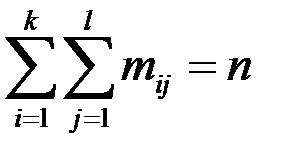n – объем выборки.

Если по данным корреляционной таблицы построить законы распределения для каждой компоненты X и Y, то числовые характеристики выборки можно найти по формулам: