Абсолютная и условная сходимость рядов.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из модулей его слагаемых:
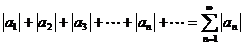
Знакопеременный ряд называется условно сходящимся, если он сходится, но ряд из модулей его слагаемых расходится.
Степенные ряды. Интервал сходимости степенного ряда.
Разложение функций в степенные ряды.
Степенным рядом называется ряд вида:
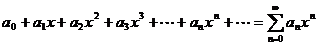 ,
,
где 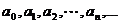 называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда.
Придавая х различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений х, при которых степенной ряд сходится, называется областью его сходимости. Это множество всегда не пусто, так как любой степенной ряд сходится при 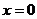 .
.
Очевидно, что частичная сумма степенного ряда
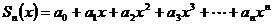
является функцией переменной х. Поэтому и сумма ряда S также является некоторой функцией переменной х, определенной в области сходимости ряда: 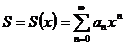 .
.
Рассмотрим теорему, имеющую важное значение в теории степенных рядов и касающуюся области сходимости степенного ряда.
Теорема Абеля. (Абель Нильс Хенрик (1802—1829) — норвежский математик).
1) Если степенной ряд сходится при 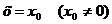 , то он сходится, и притом абсолютно, для всех х, удовлетворяющих условию
, то он сходится, и притом абсолютно, для всех х, удовлетворяющих условию 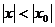 ;
;
2) если степенной ряд расходится при 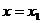 , то он расходится для всех х, удовлетворяющих условию
, то он расходится для всех х, удовлетворяющих условию 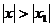 .
.
Теорема Абеля утверждает, что если 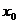 - точка сходимости степенного ряда, то во всех точках, расположенных на интервале (
- точка сходимости степенного ряда, то во всех точках, расположенных на интервале ( 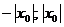 ) этот ряд сходится абсолютно, а если
) этот ряд сходится абсолютно, а если 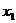 - точка расходимости степенного ряда, то во всех точках, расположенных вне интервала (
- точка расходимости степенного ряда, то во всех точках, расположенных вне интервала ( 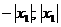 ) ряд расходится.
) ряд расходится.
Отсюда вытекает следующая теорема:
Если ряд 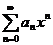 сходится не при всех значениях х и не только при
сходится не при всех значениях х и не только при 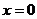 , то существует число
, то существует число 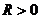 такое, что ряд абсолютно сходится при
такое, что ряд абсолютно сходится при 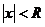 и расходится npu
и расходится npu 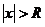 .
.
Интервал 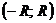 называется интервалом сходимости степенного ряда. Число R называется радиусом сходимостистепенного ряда. Отметим, что интервал сходимости у некоторых рядов охватывает всю числовую прямую (в этом случае пишут
называется интервалом сходимости степенного ряда. Число R называется радиусом сходимостистепенного ряда. Отметим, что интервал сходимости у некоторых рядов охватывает всю числовую прямую (в этом случае пишут 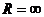 ), у других вырождается в одну точку (
), у других вырождается в одну точку ( 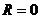 ).
).
Итак, всякий степенной ряд имеет свой радиус сходимости R. При 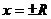 ряд может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.
ряд может либо сходиться, либо расходиться. Этот вопрос решается для каждого конкретного ряда.
Приведем способ определения радиуса сходимости степенного ряда по признаку Даламбера.
Если существует предел 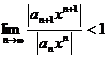 , то радиус сходимости ряда
, то радиус сходимости ряда 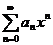 равен
равен 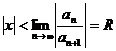 .
.
Свойства степенных рядов.
Пусть функция 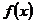 является суммой степенного ряда
является суммой степенного ряда
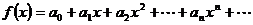 ,
,
интервал сходимости которого 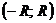 .
.
В этом случае говорят, что на интервале 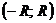 функция
функция 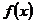 разлагается в степенной ряд (или в ряд по степеням х).
разлагается в степенной ряд (или в ряд по степеням х).
Имеют место две теоремы о свойствах степенных рядов.
Если функция 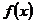 на интервале
на интервале 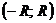 разлагается в степенной ряд, то она дифференцируема на этом интервале и ее производная
разлагается в степенной ряд, то она дифференцируема на этом интервале и ее производная 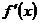 может быть найдена почленным дифференцированием ряда, т.е.:
может быть найдена почленным дифференцированием ряда, т.е.:
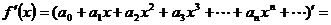
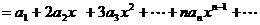 .
.
Аналогично могут быть вычислены производные любого порядка функции 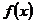 . При этом соответствующие ряды имеют тот же интервал сходимости, что и степенной ряд.
. При этом соответствующие ряды имеют тот же интервал сходимости, что и степенной ряд.
Если функция 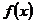 на интервале
на интервале 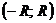 разлагается в степенной ряд, то она интегрируема в интервале
разлагается в степенной ряд, то она интегрируема в интервале 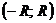 и интеграл от нее может быть вычислен почленным интегрированием степенного ряда, т.е., если
и интеграл от нее может быть вычислен почленным интегрированием степенного ряда, т.е., если 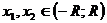 , то:
, то:
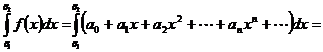
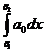 +
+
+ 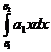 +
+ 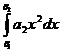 … +
… + 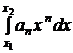 +....
+....
Теорема.Если функция 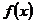 на интервале
на интервале 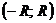 разлагается в степенной ряд:
разлагается в степенной ряд:
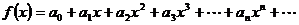 ,
,
тоэто разложение единственно.
Пусть функция 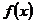 бесконечное число раз дифференцируема в точке
бесконечное число раз дифференцируема в точке 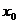 , тогда в окрестности этой точки функция раскладывается в степенной ряд:
, тогда в окрестности этой точки функция раскладывается в степенной ряд:
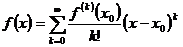 ,
,
называемый рядом Тейлора.
При 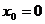 функция
функция 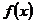 разлагается в степенной ряд:
разлагается в степенной ряд:
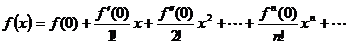 ,
,
называемый рядом Маклорена.
Для того чтобы ряд Маклорена сходился на 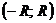 и имел своей суммой функцию
и имел своей суммой функцию 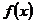 , необходимо и достаточно, чтобы на
, необходимо и достаточно, чтобы на 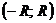 остаточный член
остаточный член 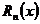 формулы Маклорена стремился к нулю при
формулы Маклорена стремился к нулю при 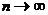 , т.е.
, т.е. 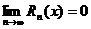 для любого
для любого 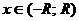 .
.
Рассмотрим разложения в ряд Маклорена некоторых элементарных функций:
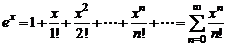 ;
;
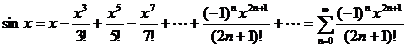
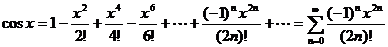 ;
;
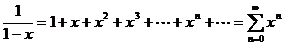 ;
;
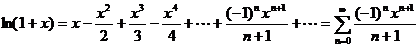
Задания на контрольную работу №4
№№ 1.1-1.30.Найдите общее решение дифференциального уравнения первого порядка.
1.1. a) 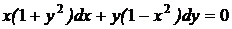 ; b) ; b) 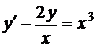 . . | 1.16.a) 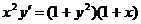 ; b) ; b) 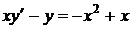 . . |
1.2. a) 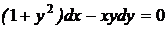 ; b) ; b) 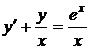 . . | 1.17.a) 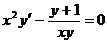 ; b) ; b) 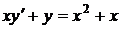 . . |
1.3. a) 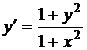 ; b) ; b) 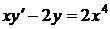 . . | 1.18a) 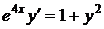 ; b) ; b) 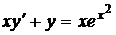 . . |
1.4. a) 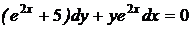 ; b) ; b) 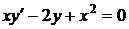 . . | 1.19.a) 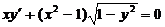 ; b) ; b) 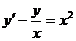 . . |
1.5. a) 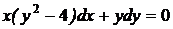 ; b) ; b) 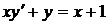 . . | 1.20.a) 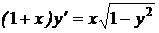 ; b) ; b) 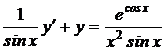 . . |
1.6. a) 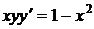 ; b) ; b) 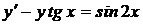 . . | 1.21.a) 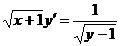 ; b) ; b) 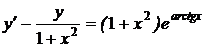 . . |
1.7. a) 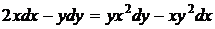 ; b) ; b) 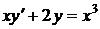 . . | 1.22.a) 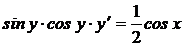 ; b) ; b) 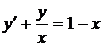 . . |
1.8. a) 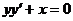 ; b) ; b) 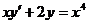 . . | 1.23.a) 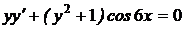 ; b) ; b) 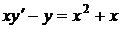 . . |
1.9. a) 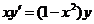 ; b) ; b) 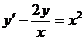 . . | 1.24.a) 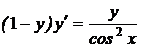 ; b) ; b) 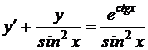 . . |
1.10. a) 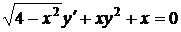 ; b) ; b) 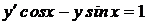 . . | 1.25.a) 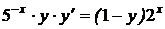 ; b) ; b) 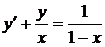 . . |
1.11.a) 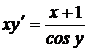 ; b) ; b) 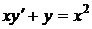 . . | 1.26.a) 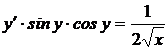 ; b) ; b) 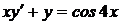 . . |
1.12a) 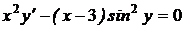 ; b) ; b) 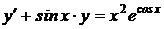 . . | 1.27.a) 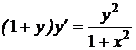 ; b) ; b) 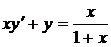 . . |
1.13.a) 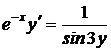 ; b) ; b) 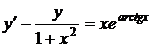 . . | 1.28.a) 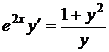 ; b) ; b) 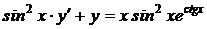 . . |
1.14.a) 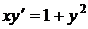 ; b) ; b) 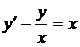 . . | 1.29.a) 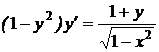 ; b) ; b) 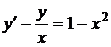 . . |
1.15. .a) 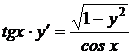 ; b) ; b) 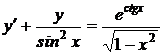 . . | 1.30.a) 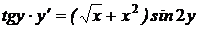 ; b) ; b) 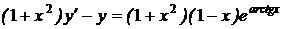 . . |
№№ 2.1-2.30. Для данного дифференциального уравнения второго порядка
найдите частное решение, удовлетворяющее заданным начальным условиям.
| 2.1. | 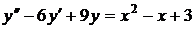 ; ; | 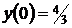 ; ; | 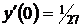 . . |
| 2.2. | 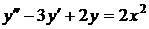 ; ; |  0; 0; |  0. 0. |
| 2.3. | 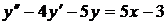 ; ; |  2; 2; |  -1. -1. |
| 2.4. | 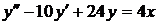 ; ; |  0; 0; |  3. 3. |
| 2.5. | 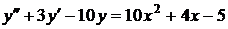 ; ; |  1; 1; |  1. 1. |
| 2.6. | 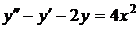 ; ; |  1; 1; |  1. 1. |
| 2.7. | 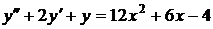 ; ; |  0; 0; |  1. 1. |
| 2.8. | 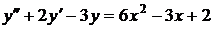 ; ; |  1; 1; |  1. 1. |
| 2.9. | 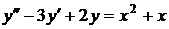 ; ; |  2; 2; |  1. 1. |
| 2.10. | 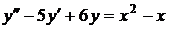 ; ; |  1; 1; |  0. 0. |
| 2.11. | 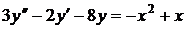 ; ; |  1; 1; |  0. 0. |
| 2.12. | 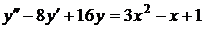 ; ; |  0; 0; |  1. 1. |
| 2.13. | 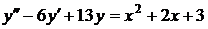 ; ; | 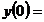 -1; -1; |  2. 2. |
| 2.14. | 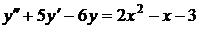 ; ; |  2; 2; |  0. 0. |
| 2.15. | 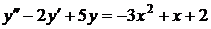 ; ; |  0; 0; |  -2. -2. |
| 2.16. | 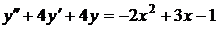 ; ; |  -2; -2; |  -1. -1. |
| 2.17. | 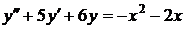 ; ; |  1; 1; |  0. 0. |
| 2.18. | 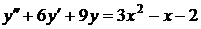 ; ; |  0; 0; |  1. 1. |
| 2.19. | 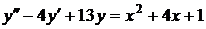 ; ; |  1; 1; |  2. 2. |
| 2.20. | 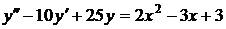 ; ; |  2; 2; |  0. 0. |
| 2.21. | 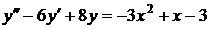 ; ; |  0; 0; |  -2. -2. |
| 2.22. | 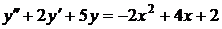 ; ; |  -2; -2; |  -1. -1. |
| 2.23. | 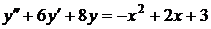 ; ; |  1; 1; |  0. 0. |
| 2.24. | 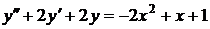 ; ; |  0; 0; |  1. 1. |
| 2.25. | 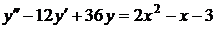 ; ; |  -1; -1; |  2. 2. |
| 2.26. | 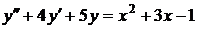 ; ; |  2; 2; |  0. 0. |
| 2.27. | 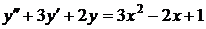 ; ; |  0; 0; |  -2. -2. |
| 2.28. | 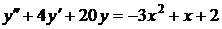 ; ; |  -2; -2; |  1. 1. |
| 2.29. | 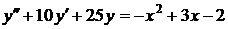 ; ; |  1; 1; |  -1. -1. |
| 2.30. | 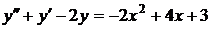 ; ; |  0; 0; |  2. 2. |
№№ 3.1-3.30. Исследуйте числовой ряд на сходимость.
3.1. 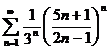 . 3.2. . 3.2. 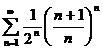 . 3.3. . 3.3. 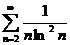 . 3.4. . 3.4. 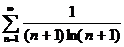 . 3.5. . 3.5. 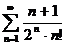 . 3.6. . 3.6. 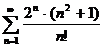 . 3.7. . 3.7. 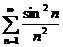 . 3.8. . 3.8. 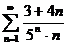 . 3.9. . 3.9. 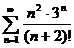 . 3.10. . 3.10. 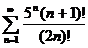 . . | 3.11. 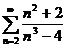 . 3.12. . 3.12. 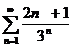 . 3.13. . 3.13. 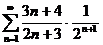 . 3.14. . 3.14. 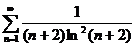 . 3.15. . 3.15. 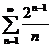 . 3.16. . 3.16. 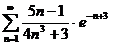 . 3.17. . 3.17. 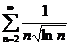 . 3.18. . 3.18. 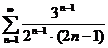 . 3.19. . 3.19. 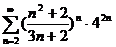 . 3.20. . 3.20. 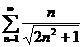 . . | 3.21. 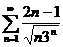 . 3.22. . 3.22. 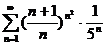 . 3.23. . 3.23. 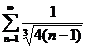 . 3.24. . 3.24. 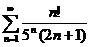 . 3.25. . 3.25. 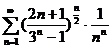 . 3.26. . 3.26. 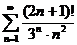 . 3.27. . 3.27. 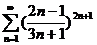 . 3.28. . 3.28. 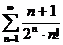 . 3.29. . 3.29. 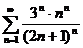 . 3.30. . 3.30. 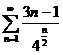 . . |
№№ 4.1-4.30. Найдите область сходимости данного ряда.
| 4.1 | 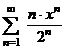 ; ; | 4.2 | 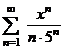 ; ; |
| 4.3 | 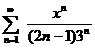 ; ; | 4.4 | 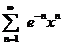 ; ; |
| 4.5 | 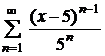 ; ; | 4.6 | 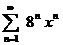 ; ; |
| 4.7 | 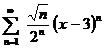 ; ; | 4.8 | 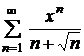 ; ; |
| 4.9 | 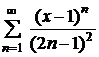 ; ; | 4.10 | 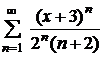 ; ; |
| 4.11 | 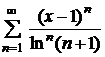 ; ; | 4.12 | 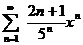 ; ; |
| 4.13 | 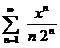 ; ; | 4.14 | 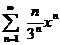 ; ; |
| 4.15 | 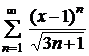 ; ; | 4.16 | 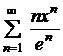 ; ; |
| 4.17 | 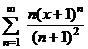 ; ; | 4.18 | 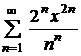 ; ; |
| 4.19 | 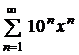 ; ; | 4.20 | 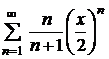 ; ; |
| 4.21 | 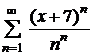 ; ; | 4.22 | 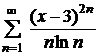 ; ; |
| 4.23 | 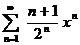 ; ; | 4.24 | 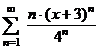 ; ; |
| 4.25 | 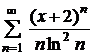 ; ; | 4.26 | 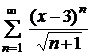 ; ; |
| 4.27 | 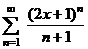 ; ; | 4.28 | 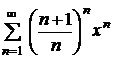 ; ; |
| 4.29 | 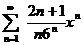 ; ; | 4.30 | 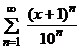 . . |
№№ 5.1-5.30. Вычислите определенный интеграл с точностью до 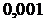 , разлагая подынтегральную функцию в ряд и затем интегрируя его почленно.
, разлагая подынтегральную функцию в ряд и затем интегрируя его почленно.
5.1. 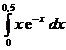 . . | 5.11. 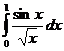 . . | 5.21. 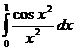 . . |
5.2. 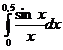 . . | 5.12. 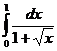 . . | 5.22. 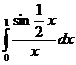 . . |
5.3. 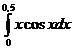 . . | 5.13. 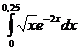 . . | 5.23. 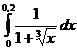 . . |
5.4. 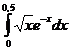 . . | 5.14. 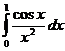 . . | 5.24. 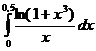 . . |
5.5. 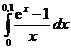 . . | 5.15. 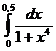 . . | 5.25. 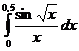 . . |
5.6. 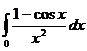 . . | 5.16. 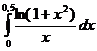 . . | 5.26. 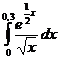 |
5.7. 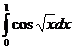 . . | 5.17. 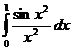 . . | 5.27. 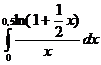 . . |
5.8. 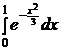 . . | 5.18. 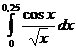 . . | 5.28. 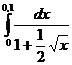 . . |
5.9. 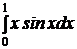 . . | 5.19. 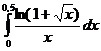 . . | 5.29. 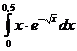 . . |
5.10. 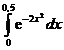 . . | 5.20. 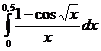 . . | 5.30. 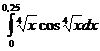 . . |
Примеры решения заданий контрольной работы №4
Задание №1
a)Найти общее решение уравнения 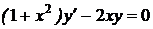
Решение: 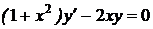 ,
, 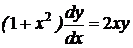 ;
; 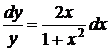 .
.
Интегрируя последнее уравнение, найдем 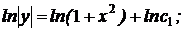 .
.
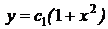 - общее решение уравнения.
- общее решение уравнения.
b) Найти общее решение уравнения 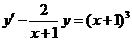 .
.
Решение. Сделаем подстановку 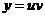 , где
, где 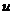 и
и 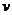 — неизвестные пока функции от
— неизвестные пока функции от 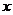 . Тогда
. Тогда 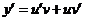 и уравнение принимает вид:
и уравнение принимает вид:
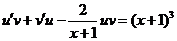 или
или 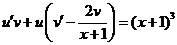 (9)
(9)
Выбираем 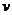 так, чтобы
так, чтобы 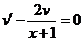 . Решаем это уравнение
. Решаем это уравнение 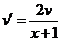 ,
, 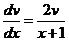 ;
; 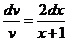 ; интегрируя получим:
; интегрируя получим: 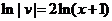 ;
; 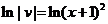 ;
; 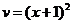 . Подставляя это значение в равенство (9) получим:
. Подставляя это значение в равенство (9) получим:
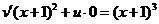 ;
; 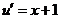 ;
; 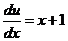 ;
; 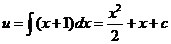 .
.
Таким образом, 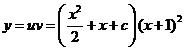 — общее решение данного уравнения.
— общее решение данного уравнения.
Задание №2
Найти частное решение уравнения 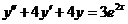 ,удовлетворяющее начальным условиям
,удовлетворяющее начальным условиям 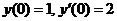 .
.
Решение.Данное уравнение — это уравнение вида (10), при 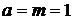 ,
, 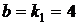 ,
, 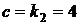 ,
, 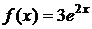 .
.
Найдем сначала общее решение данного уравнения 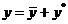 .
.
Для этого решим соответствующее однородное уравнение:
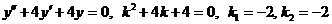 . Следовательно
. Следовательно 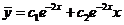 .
.
Так как числа 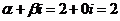 нет среди корней характеристического уравнения, то частное решение
нет среди корней характеристического уравнения, то частное решение 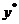 подбираем в таком же виде, как и правая часть
подбираем в таком же виде, как и правая часть 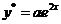 ,
, 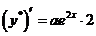 ,
, 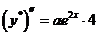 . Подставляем эти значения в уравнение
. Подставляем эти значения в уравнение 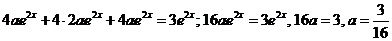 .
.
Следовательно, 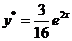 . Значит,
. Значит, 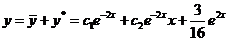 - общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем:
- общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем:
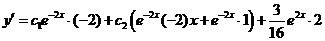 . Так как
. Так как 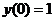 и
и 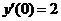 , то получаем
, то получаем
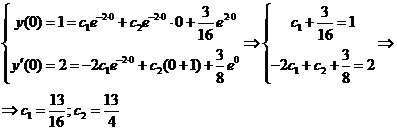
Подставляя эти значения в общее решение, найдем частное решение 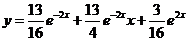 , удовлетворяющее заданным начальным условиям.
, удовлетворяющее заданным начальным условиям.
Задание №3
Исследовать на сходимость ряд: 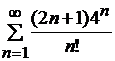 .
.
Решение:
Имеем 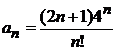 ,
, 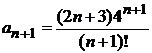 . По признаку Даламбера находим предел:
. По признаку Даламбера находим предел:
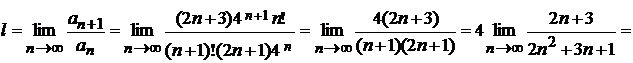
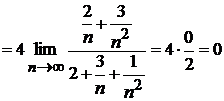 , т.к. l<1, то ряд сходится.
, т.к. l<1, то ряд сходится.
Задание №4
Найдите область сходимости степенного ряда 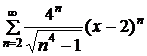
Решение.
Найдем радиус сходимости:
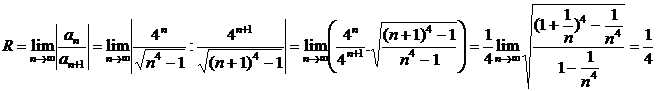 . Следовательно, интервал сходимости:
. Следовательно, интервал сходимости:
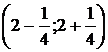 или
или 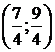 .
.
Исследуем сходимость на концах интервала:
1) 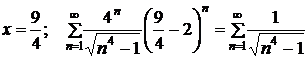 . (1)
. (1)
Для исследования ряда (1) применим предельный признак сравнения с гармоническим рядом 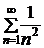 .
.
Проверим выполнение признака:
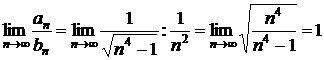 .
.
Так как предел конечный и отличный от нуля, то ряд (1) сходится, так как сходится при s =2> 1 гармонический ряд.
2) 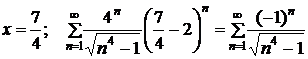 . (2)
. (2)
Применим к исследованию знакочередующегося ряда (2) признак Лейбница.
Так как абсолютные величины ряда (2) монотонно убывают и 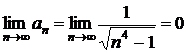 ,
, 
то по признаку сходимости Лейбница данный ряд сходится.
Ответ: область сходимости 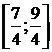 .
.
Задание №5
Вычислить определенный интеграл 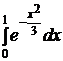 с точностью до 0,001.
с точностью до 0,001.
Решение. Разложим подынтегральную функцию в ряд. Имеем:
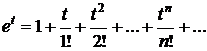
Заменяя t = 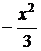 , получим:
, получим:
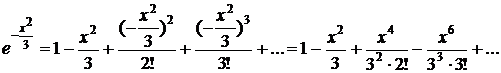
Подставляя разложение подынтегральной функции в интеграл, получаем:
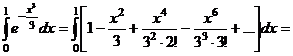
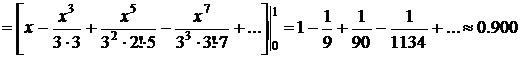
При вычислениях можно ограничиться первыми тремя членами ряда, так как четвертый член знакочередующегося ряда меньше 0,001 и поэтому сумма ряда, начинающегося с четвертого члена, будет меньше 0,001 и весь этот ряд можно отбросить.
