Приложения определенного интеграла.
В декартовой системе координат за основную фигуру, площадь которой выражается определенным интегралом, принимается криволинейная трапеция. Если y=f(x) – уравнение линии, ограничивающей трапецию, то площадь трапеции S (в предположении, что y³0) равна S= 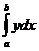 , где пределы интегрирования a и b(a<b) - абсциссы начала и конца линии.
, где пределы интегрирования a и b(a<b) - абсциссы начала и конца линии.
Если линия задана параметрическими уравнениями x=j(t), y=y(t), то совершая подстановку в интеграле по формуле x=j(t), получим
S= 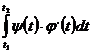 ,
,
где t1 и t2- значения, между которыми изменяется параметр t, когда точка пробегает слева направо всю линию, ограничивающую трапецию сверху.

 Пусть дано тело, ограниченное замкнутой поверхностью, пусть известна площадь любого его сечения, проведенного плоскостью, перпендикулярной к некоторой прямой, например к оси абсцисс:
Пусть дано тело, ограниченное замкнутой поверхностью, пусть известна площадь любого его сечения, проведенного плоскостью, перпендикулярной к некоторой прямой, например к оси абсцисс:
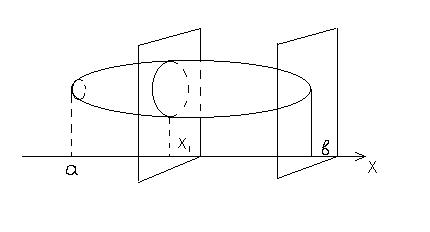
При этом можно считать, что площадь такого сечения является известной нам функцией S(x), где x – абсцисса точки пересечения указанной плоскости с осью х. Далее предполагается, что все тело заключено между двумя перпендикулярными к оси х плоскостями, пересекающими ее в точках a и b (a<b). Для определения объема такого тела разобьем его на слои с помощью секущих плоскостей, перпендикулярных к оси х и пересекающих ее в точках x0=a, x2,…, xn=b. Каждый слой заменим цилиндром с той же высотой и основанием, равным S(x). Объем прямого цилиндра равен произведению площади его основания на высоту. Объем вычисляют как предел при n®¥ суммы объемов, образующих ступенчатое тело и получаем
V= 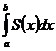
Если тело получено вращением криволинейной трапеции, ограниченной линией y=f(x), вокруг оси Ох, то поперечным сечением с абсциссой х служит круг, радиус которого равен соответствующей ординате линии y=f(x)
S(x)=py2 Þ Vx= 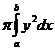 , где y=f(x).
, где y=f(x).
Получена формула объема тела, полученного вращением линии y=f(x) вокруг оси Ох. Аналогично получается формула объема тела, полученного вращением трапеции вокруг оси Оу. Там возможны две формулы:
Vy= 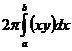 или Vy=
или Vy= 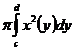 , где c и d на оси Оу.
, где c и d на оси Оу.
Длина дуги AB кривой y=f(x) есть предел длины вписанной в нее ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих сторон к нулю:
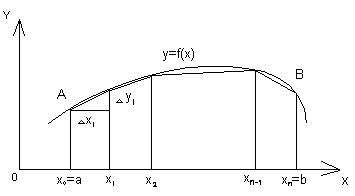
Линия AB задана уравнением y=f(x). Длина дуги AB вычисляется по формуле
L= 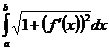 или L=
или L= 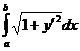 .
.
Если dx внести под знак корня, то формулу можно переписать в виде
L= 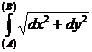 .
.
Если уравнение линии задано параметрически: x=x(t), y=y(t) и t1,t2 – значение параметра t, соответствующие концам дуги, причем t1<t2, то
L= 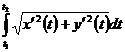

Задания на контрольную работу № 3
№№ 1.1-1.30. Найдите интегралы.
1.1 a) 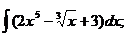 | 1.11 a) 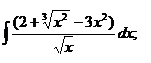 | 1.21 a) 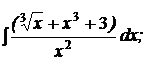 |
b) 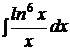 ; ; | b) 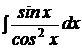 ; ; | b) 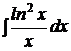 ; ; |
c) 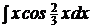 ; ; | c) 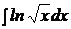 ; ; | c) 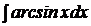 ; ; |
d) 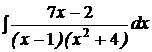 ; ; | d) 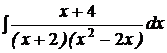 ; ; | d) 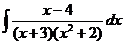 ; ; |
e) 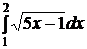 ; ; | e) 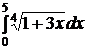 ; ; | e) 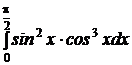 ; ; |
1.2. a) 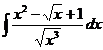 ; ; | 1.12 a) 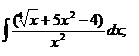 | 1.22a) 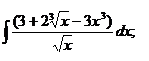 |
b) 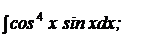 | b) 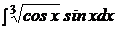 ; ; | b) 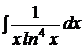 ; ; |
c) 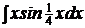 ; ; | c) 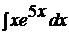 ; ; | c) 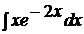 ; ; |
d) 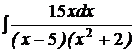 ; ; | d) 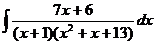 ; ; | d) 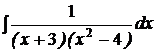 ; ; |
e) 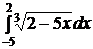 ; ; | e) 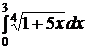 ; ; | e) 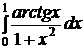 ; ; |
1.3.a) 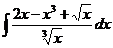 ; ; | 1.13 a) 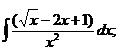 | 1.23 a) 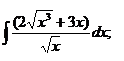 |
b) 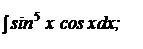 | b) 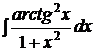 ; ; | b) 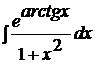 ; ; |
c) 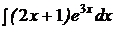 ; ; | c) 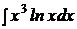 ; ; | c) 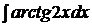 ; ; |
d) 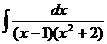 ; ; | d) 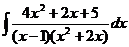 ; ; | d) 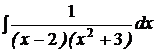 ; ; |
e) 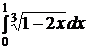 ; ; | e) 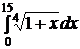 ; ; | e) 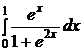 ; ; |
1.4. a) 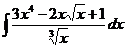 ; ; | 1.14 a) 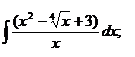 | 1.24 a) 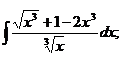 |
b) 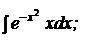 | b) 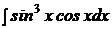 ; ; | b) 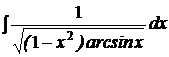 ; ; |
c) 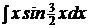 ; ; | c) 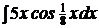 ; ; | c)  ; ; |
d) 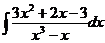 ; ; | d) 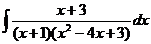 ; ; | d) 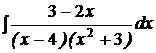 ; ; |
e) 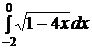 ; ; | e) 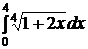 ; ; | e) 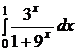 ; ; |
1.5. a) 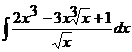 ; ; | 1.15 a) 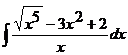 ; ; | 1.25 a) 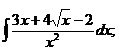 |
b) 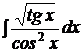 ; ; | b) 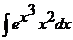 ; ; | b) 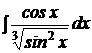 ; ; |
c) 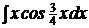 ; ; | c) 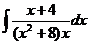 ; ; | c) 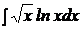 ; ; |
d) 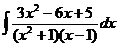 ; ; | d)  ; ; | d) 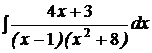 ; ; |
e) 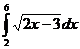 ; ; | e) 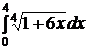 ; ; | e) 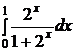 ; ; |
1.6.a) 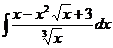 ; ; | 1.16 a) 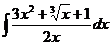 ; ; | 1.26 a) 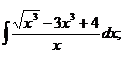 |
b) 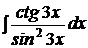 ; ; | b) 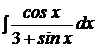 ; ; | b) 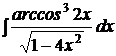 ; ; |
c) 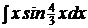 ; ; | c) 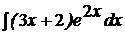 ; ; | c) 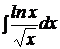 ; ; |
d) 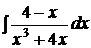 ; ; | d) 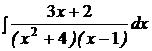 ; ; | d) 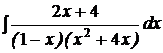 ; ; |
e) 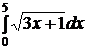 ; ; | e) 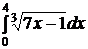 ; ; | e) 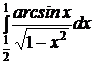 ; ; |
1.7.a) 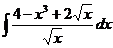 ; ; | 1.17 a) 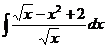 ; ; | 1.27 a) 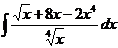 ; ; |
b) 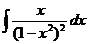 ; ; | b) 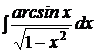 ; ; | b) 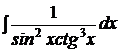 ; ; |
c) 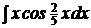 ; ; | c) 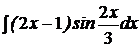 ; ; | c) 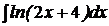 ; ; |
d) 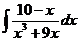 ; ; | d) 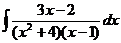 ; ; | d) 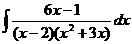 ; ; |
e) 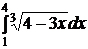 ; ; | e) 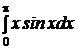 ; ; | e) 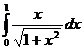 ; ; |
1.8. a) 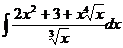 ; ; | 1.18 a) 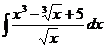 ; ; | 1.28 a) 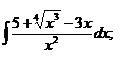 |
b) 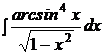 ; ; | b) 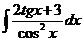 ; ; | b) 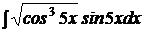 ; ; |
c) 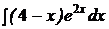 ; ; | c) 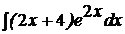 ; ; | c) 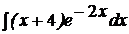 ; ; |
d) 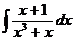 ; ; | d) 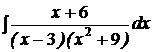 ; ; | d) 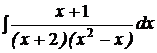 ; ; |
e) 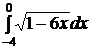 ; ; | e) 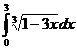 ; ; | e) 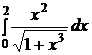 ; ; |
1.9. a) 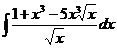 ; ; | 1.19 a) 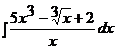 ; ; | 1.29 a) 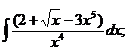 |
b) 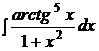 ; ; | b) 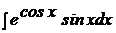 ; ; | b) 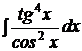 ; ; |
c) 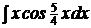 ; ; | c)  ; ; | c) 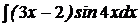 ; ; |
d) 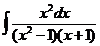 ; ; | d) 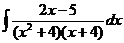 ; ; | d) 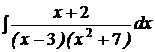 ; ; |
e) 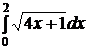 ; ; | e) 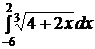 ; ; | e) 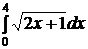 ; ; |
1.10. a) 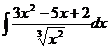 ; ; | 1.20 a) 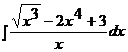 ; ; | 1.30a) 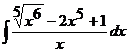 ; ; |
b) 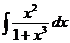 ; ; | b) 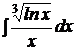 ; ; | b) 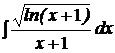 ; ; |
c) 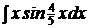 ; ; | c) 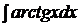 ; ; | c) 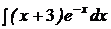 ; ; |
d) 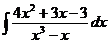 ; ; | d) 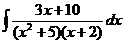 ; ; | d) 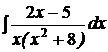 ; ; |
e) 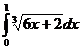 ; ; | e) 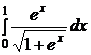 ; ; | e) 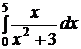 ; ; |
№№ 2.1-2.30. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
№№ 3.1-3.30. Вычислите несобственные интегралы или докажите их расходимость.
№№ 4.1-4.30. Произвести вычисления. 4.1.Вычислите площадь фигуры, ограниченной параболой 4.2.Вычислите длину дуги кривой 4.3. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми 4.4.Вычислите площадь фигуры, ограниченной линией 4.5.Вычислите длину дуги арки циклоиды 4.6.Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболой 4.7.Вычислите длину дуги кривой 4.8. Вычислите площадь фигуры, ограниченной линиями 4.9. Вычислите длину дуги полукубической параболы 4.10. Вычислите площадь фигуры, ограниченной линией 4.11. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линией 4.12. Вычислите длину дуги полукубической параболы 4.13. Вычислите площадь фигуры, ограниченной кардиоидой 4.14. Вычислите площадь фигуры, ограниченной линиями 4.15. Вычислите площадь фигуры, ограниченной одной аркой циклоиды 4.16. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми 4.17. Вычислите длину дуги кардиоиды 4.18. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболами 4.19. Вычислите площадь фигуры, ограниченной параболой 4.20. Вычислите длину астроиды 4.21. Вычислите площадь фигуры, ограниченной четырехлепестковой розой 4.22. Вычислите длину дуги кривой 4.23. Вычислите площадь фигуры, ограниченной линиями 4.24. Вычислите объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной кривыми 4.25. Вычислите площадь фигуры, ограниченной линией 4.26. Вычислите длину дуги кривой 4.27. Вычислите длину дуги данной линии 4.28. Вычислите объем тела, полученного вращением вокруг оси Оу линии 4.29. Вычислите площадь фигуры, ограниченной астроидой 4.30. Вычислите площадь фигуры, ограниченной линиями |
Пример решения заданий контрольной работы № 3
Задание №1.
a) Вычислить интеграл: 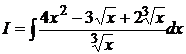
Решение:
Преобразуем подынтегральное выражение
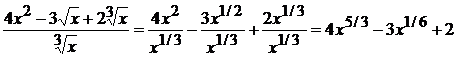 . Следовательно,
. Следовательно,
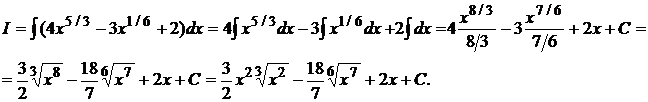
Здесь мы воспользовались свойствами неопределенного интеграла и формулами 2 и 1 таблицы интегралов. Сделаем проверку правильности интегрирования. Найдем 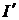 .
.
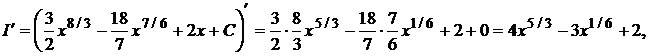
что совпадает с преобразованным подынтегральным выражением.
b) Вычислить интеграл: 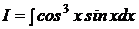
Решение:
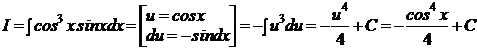
Проверка: 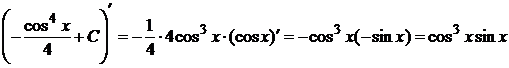 ,
,
что совпадает с подынтегральным выражением.
c) Вычислить: 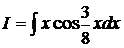 .
.
Решение:
Все необходимые вычисления будем проводить одновременно с применением формулы 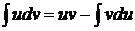
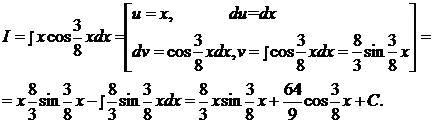
d) Вычислить интеграл: 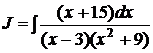 .
.
Решение:
Разложим подынтегральную дробь на простейшие дроби:
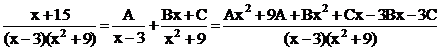 .
.
Следовательно х + 15 º (А + В)х2 + (С – 3В)х + 9А – 3С.
Сравним коэффициенты при одинаковых степенях х в левой и правой частях:
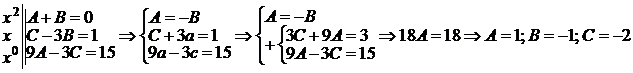
Итак:
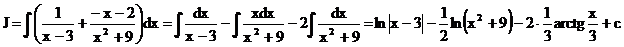 .e) Вычислите интеграл
.e) Вычислите интеграл 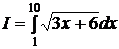
Решение:
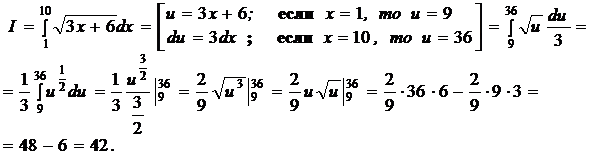
Задание 2. Вычислить определенный интеграл
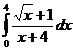
Решение. 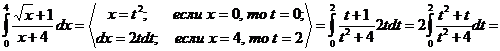
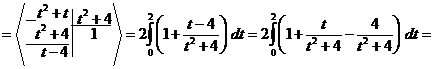
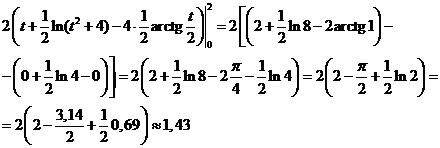
При вычислении этого интеграла были применены формулы
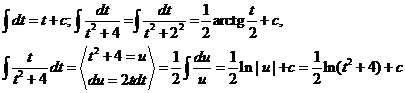
Задание 3 Вычислить несобственный интеграл 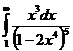 или доказать его расходимость
или доказать его расходимость
Решение.
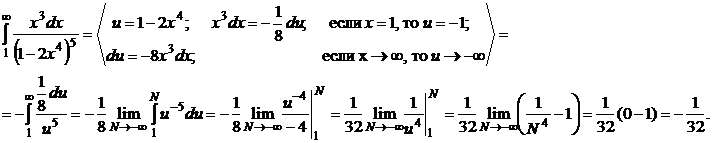
Таким образом, несобственный интеграл равен 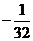 , т. е. он сходится.
, т. е. он сходится.
Задание 4Найти площадь фигуры, ограниченной линиями 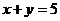 ,
, 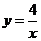
Решение. Первое уравнение определяет на плоскости прямую линию, второе – гиперболу (рис. 2).
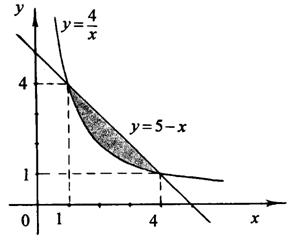
рис. 2
Найдем их точки пересечения
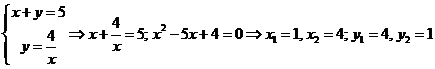
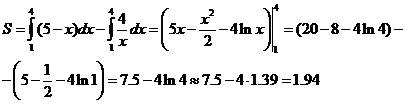

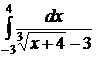 ;
; 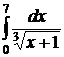 ;
; 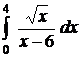 ;
; 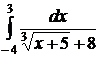 ;
; 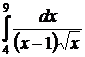 ;
; 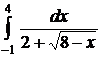 ;
; 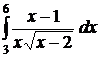 ;
; 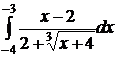 ;
; 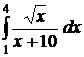 ;
; 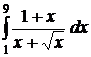 ;
; 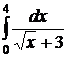 ;
; 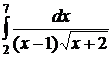 ;
; 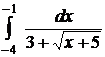 ;
; 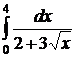 ;
; 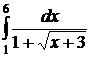 ;
; 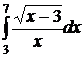
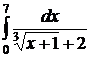 ;
; 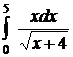 ;
; 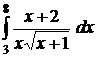 ;
; 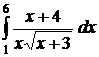 ;
; 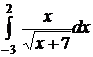 ;
; 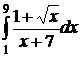 ;
; 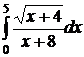 ;
; 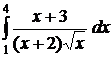 ;
; 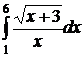 ;
; 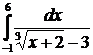 ;
; 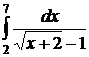 ;
; 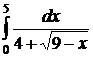
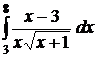 ;
; 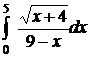 .
. 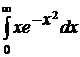
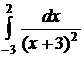
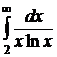
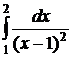
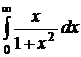
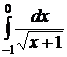
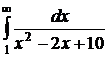
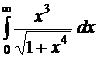
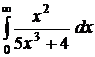
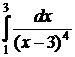
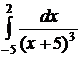
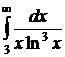 .
. 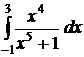
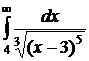
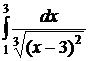
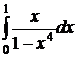 .
. 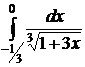
 .
. 
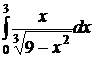
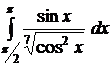
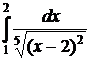 .
. 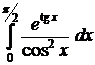 .
. 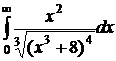
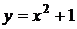 и прямой
и прямой 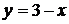 .
.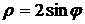 .
.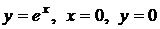 ,x=1.
,x=1.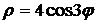 .
.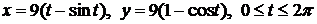 .
.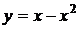 и прямой
и прямой 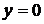 .
.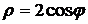 .
.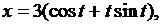
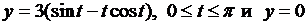 .
.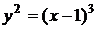 от точки
от точки 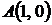 до точки
до точки  .
.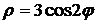 .
. .
.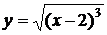 от точки
от точки 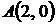 до точки
до точки 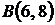 .
.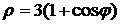 .
.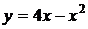 и
и 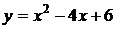 .
.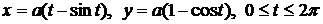 и осью Ох.
и осью Ох.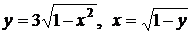 и осью Оу
и осью Оу 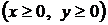 .
.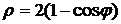 .
.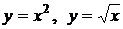 .
.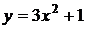 и прямой
и прямой 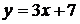 .
.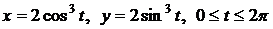 .
.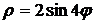 .
.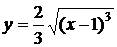 , ограниченной прямыми
, ограниченной прямыми 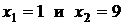 .
.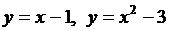 .
.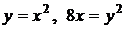 .
.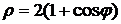 .
.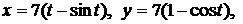
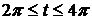 .
.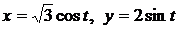 .
.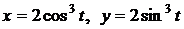 .
.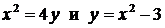 .
.