Физические приложения определенного интеграла

Лекция 21 Приложения определенного интеграла (2ч)

Содержание лекции: Геометрические и физические приложения определенного интеграла: вычисление площадей плоских фигур, объемов тел вращения, длины дуги, массы прямолинейного стержня, работы силы.

Геометрические приложения

а) Площадь фигуры

Как уже отмечалось в лекции 19, 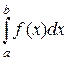численно равен площади криволинейной трапеции, ограниченной кривой у = f(x) , прямыми х = а, х = b и отрезком [a, b] оси ОХ. При этом если f(x) £ 0 на [a, b], то интеграл следует взять со знаком минус.

Если же на заданном отрезке функция у = f(x) меняет знак, то для вычисления площади фигуры, заключенной между графиком этой функции и осью ОХ, следует разбить отрезок на части, на каждой из которых функция сохраняет знак, и найти площадь каждой части фигуры. Искомая площадь в этом случае есть алгебраическая сумма интегралов по этим отрезкам, причем интегралы, соответствующие отрицательным значения функции, взяты в этой сумме со знаком «минус».

Если фигура ограничена двумя кривыми у = f₁(x) и у = f₂(x), f₁(x)£f₂(x), то, как следует из рис.9, ее площадь равна разности площадей криволинейных трапеций аВСb и аАDb , каждая из которых численно равна интегралу. Значит,

.

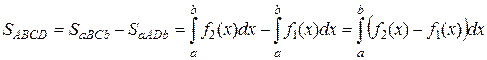Заметим, что площадь фигуры, изображенной на рисунке 10,а находятся по такой же формуле: S = 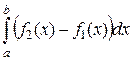(докажите это!). Подумайте, как вычислить площадь фигуры, изображенной на рисунке 10,б?

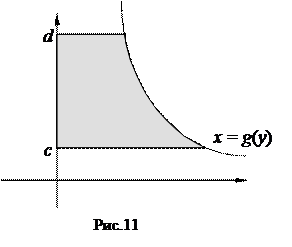
Мы вели речь только о криволинейных трапециях, прилежащих к оси ОХ. Но аналогичные формулы справедливы и для фигур, прилежащих к оси ОУ. Например, площадь фигуры, изображенной на рисунке 11, находится по формуле

S = .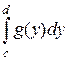

Пусть линия y = f(x), ограничивающая криволинейную трапецию, может быть задана параметрическими уравнениями 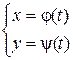, tÎ [a, b], причем j(a)=а, j(b) = b, т.е. у = 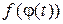. Тогда площадьэтой криволинейной трапеции равна

.

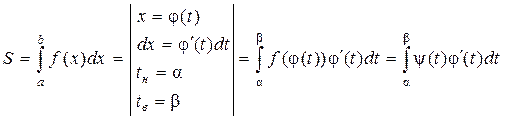б) Длина дуги кривой

Пусть дана кривая у = f(x). Рассмотрим дугу 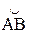этой кривой, соответствующую изменению х на отрезке [a, b]. Найдем длину этой дуги. Для этого разобьем дугу АВ на п частей точками А = М₀,М₁, М_2, ..., М_п = В (рис.14), соответствующими точкам х₁, х₂, ..., х_п Î [a, b].

Обозначим Dl_i длину дуги 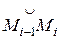, тогда l = 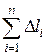. Если длины дуг Dl_i достаточно малы, то их можно считать приближенно равными длинам соответствующих отрезков 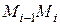, соединяющих точки М_{i-1, Mi}. Эти точки имеют координаты М_i-1(х_{i-1, f}(x_i-1)) , M_i(х_i, f(x_i)). Тогда длины отрезков равны соответственно

.

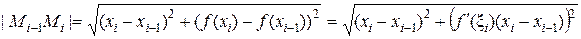Здесь использована формула Лагранжа. Положим х_i – x_i-1 =Dх_i , получим

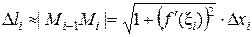
Тогда l = 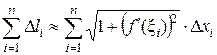, откуда

l = .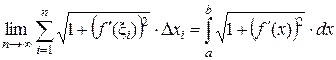

Таким образом, длина дуги кривой у = f(x), соответствующей изменению х на отрезке [a, b], находится по формуле

l = 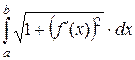, (1)

Если кривая задана параметрически 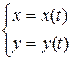, tÎ[a, b], т.е. y(t) = f(x(t)), то из формулы (1) получим:

l= .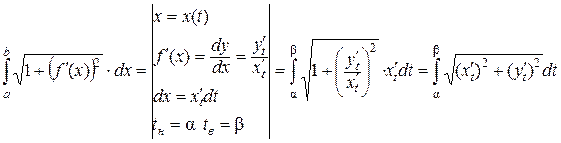

Значит, если кривая задана параметрически 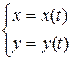, то длина дуги этой кривой, соответствующей изменению tÎ[a, b], находится по формуле

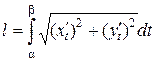
в) Объем тела вращения.

Рис.15

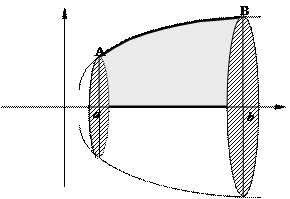Рассмотрим криволинейную трапецию аАВb , ограниченную линией у = f(x), прямыми х = а, х = b и отрезком [a, b] оси ОХ (рис.15). Пусть эта трапеция вращается вокруг оси ОХ, в результате получится тело вращения. Можно доказать, что объем этого тела будет равен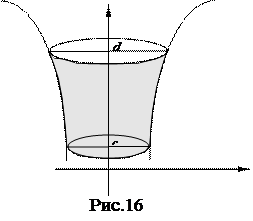

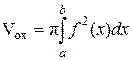
Аналогично можно вывести формулу объема тела, полученного вращением вокруг оси ОУ криволинейной трапеции, ограниченной графиком функции х = j(у), прямыми y = c , y = d и отрезком [c, d] оси ОУ (рис.15):

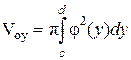
Физические приложения определенного интеграла

В лекции 19 мы доказали, что с физической точки зрения, интеграл 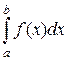численно равен массе прямолинейного тонкого неоднородного стержня длины l = b – a, с переменной линейной плотностью r = f(x), f(x) ³ 0, где х – расстояние от точки стержня до его левого конца.

Рассмотрим другие физические приложения определенного интеграла.

Задача 1. Найти работу, необходимую для выкачивания масла из вертикального цилиндрического резервуара высотой Н и радиусом основания R. Плотность масла равна r.

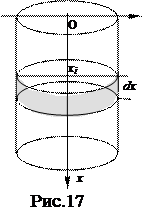Решение. Построим математическую модель данной задачи. Пусть ось ОХ проходит вдоль оси симметрии цилиндра высоты Н и радиуса R, начало – в центре верхнего основания цилиндра (рис.17). Разобьем цилиндр на п малых горизонтальных частей. Тогда 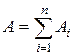, где A_i – работа по выкачиванию i-го слоя. Это разбиение цилиндра соответствует разбиению отрезка [0, H] изменения высоты слоя на п частей. Рассмотрим один из таких слоев, расположенный на расстоянии х_i от поверхности, шириной Dх (или сразу dx). Выкачивание этого слоя можно рассматривать как «поднятие» слоя на высоту х_i.

Тогда работа по выкачиванию этого слоя равна

A_i »Р_ix_i, ,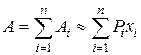

где Р_i =rgV_i = rgpR²dx, Р_i – вес, V_i – объем слоя. Тогда A_i » Р_ix_i = rgpR²dx.х_i , откуда

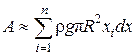, и, следовательно, .

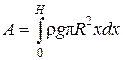Задача 2. Найти момент инерции

а) полого тонкостенного цилиндра относительно оси, проходящей через ось его симметрии;

б) сплошного цилиндра относительно оси, проходящей через ось его симметрии ;

в) тонкого стержня длины l относительно оси, проходящей через его середину;

г) тонкого стержня длины l относительно оси, проходящей через его левый конец.

Решение. Как известно, момент инерции точки относительно оси равен J=mr², а системы точек .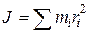

а) Цилиндр тонкостенный, значит, толщиной стенок можно пренебречь. Пусть радиус основания цилиндра R, высота его Н, плотность масс на стенках равна r.

Разобьем цилиндр на п частей и найдем 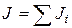, где J_i – момент инерции i-го элемента разбиения.

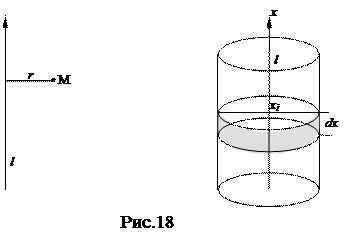
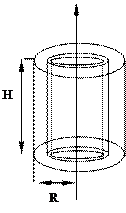Рассмотрим i-й элемент разбиения (бесконечно малый цилиндрик). Все его точки находятся на расстоянии R от оси l. Пусть масса этого цилиндрика т_i , тогда т_i = rV_i » rS_бок = 2prRdx_i, где х_i Î[0, H]. Тогда J_i » R²prRdx_i, откуда

.

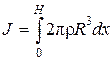Если r – постоянная, то J = 2prR³Н, а так как при этом масса цилиндра равна М = 2prRН, то J = МR².

б) Если цилиндр сплошной (заполненный), то разобьем его на п вложенных один в другого тонких цилиндров. Если п велико, каждый из этих цилиндров можно считать тонкостенным. Это разбиение соответствует разбиению отрезка [0, R] на п частей точками R_i. Найдем массу i-го тонкостенного цилиндра: т_i = rV_i, где

V_i = pR_i²Н – pR_i-1²Н = pН(R_i² –R_i-1²) =

= pН(R_i –R_i-1)(R_i +R_i-1).

Ввиду того, что стенки цилиндра тонкие, то можно считать, что R_i +R_i-1» 2R_i, а R_i –R_i-1 = DR_i , тогда V_i» pН2R_iDR_i, откуда т_i » rpН×2R_iDR_i,

а .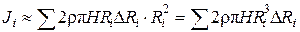

Тогда окончательно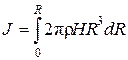

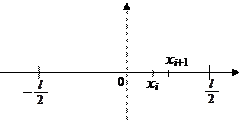в) Рассмотрим стержень длины l, плотность масс которого равна r. Пусть ось вращения проходит через его середину.

Моделируем стержень как отрезок 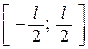оси ОХ, тогда ось вращения стержня –ось ОУ. Рассмотрим элементарный отрезок 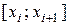, масса его 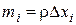, расстояние до оси можно считать приближенно равным r_i = х_i. Тогда момент инерции этого участка равен 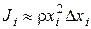, откуда момент инерции всего стержня равен 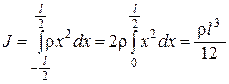. Учитывая, что масса стержня равна 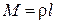, то

.

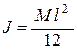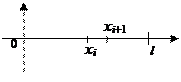г) Пусть теперь ось вращения проходит через левый конец стержня, т.е. моделью стержня является отрезок 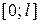оси ОХ. Тогда аналогично 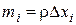, r_i = х_i, 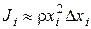, откуда 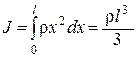, а так как 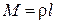, то .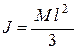

Задача 3. Найти силу давления жидкости с плотностью r на прямоугольный треугольник с катетами а и b, погруженный вертикально в жидкость так, что катет а находится на поверхности жидкости.

Решение.

Построим модель задачи. Пусть вершина прямого угла треугольника находится в начале координат, катет а совпадает с отрезком [0; a] оси ОУ (ось ОУ определяет поверхность жидкости), ось ОХ направлена вниз, катет b совпадает с отрезком [0; b] этой оси. Гипотенуза этого треугольника имеет уравнение 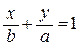, или .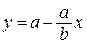

Известно, что если на горизонтальную область площади S, погруженную в жидкость плотности r, давит столб жидкости высотой h, то сила давления равна 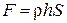(закон Паскаля). Воспользуемся этим законом.

На отрезке [0; b] оси ОХ возьмем элементарный участок 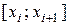. В силу того, что ширина его бесконечно мала, можно считать, что соответствующий этому отрезку элемент площади треугольника (элементарная трапеция) расположен в жидкости горизонтально на глубине х_i, а сама площадь этого элемента равна приближенно площади прямоугольника со сторонам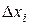и и 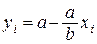, т.е. 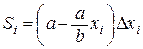. Тогда по закону Паскаля этот элементарный участок треугольника испытывает давление

.

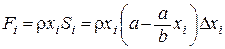Тогда приближенно давление F можно представить в виде 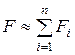, а истинное значение F равно 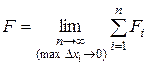, откуда искомое давление равно

.

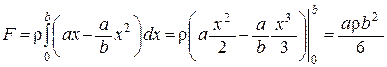Задача 4. Скорость точки при прямолинейном движении равна 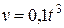м/с. Найти путь, пройденный точкой за первые 10 секунд движения.

Решение.

Известно, что скорость точки и пройденный путь при прямолинейном движении связаны соотношением 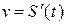или 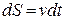. Тогда 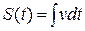. А путь, пройденный за время 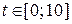есть приращение этой функции на этом отрезке, т.е. 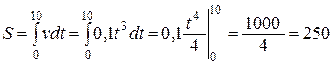м.