Прямая в пространстве. Взаимное расположение прямой

И плоскости в пространстве.

Прямая в пространстве может быть задана системой уравнений двух плоскостей

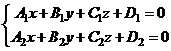, (1)

пересекающихся по этой прямой.

Уравнения (1) называются общими уравнениями прямой. Для решения задач уравнения (1) не всегда удобны, по этому используют специальный вид уравнения прямой.

Пусть дана прямая L и ненулевой вектор 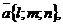лежащий на данной прямойили параллельно ей. На прямой L возьмем точку M 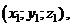тогда уравнение этой прямой можно записать следующим образом

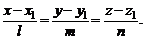(2)

Уравнение (2) называется каноническим уравнением прямой.

От канонических уравнений прямой, введя параметр легко можно перейти к параметрическим уравнением:

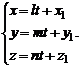(3)

Пусть заданы две прямые каноническими уравнениям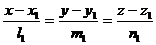и.

и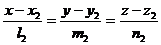

При любом расположении этих прямых в пространстве, один из двух углов между ними равен углу 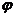между их направляющими векторами 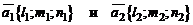. Угол 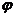можно вычислить по формуле

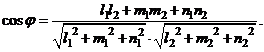(4)

Условие параллельности и перпендикулярности двух прямых в пространстве имеют следующий вид

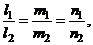(5)

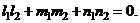(6)

Рассмотрим теперь взаимное расположение прямой 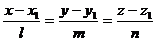и плоскости Ax+By+Cz+D=0.

Угол между прямой и плоскостью определяется по формуле

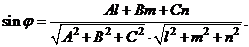(7)

Условием параллельности прямой и плоскости является условие

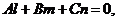(8)

а условием перпендикулярности прямой и плоскости

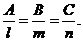(9)

Задания на контрольную работу № 1

№№1.1-1.30.Даны числа a, b и матрицы А, В, С. Найдите .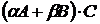

1.1. ,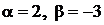

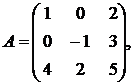
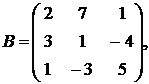
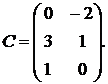
1.2. ,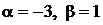

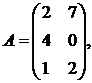
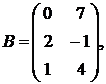
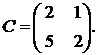
1.3. ,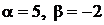

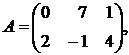
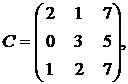
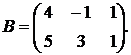
1.4. ,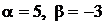

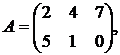
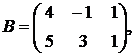
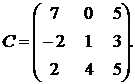
1.5. ,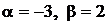

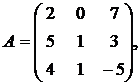
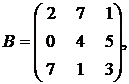
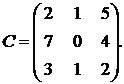
1.6. ,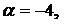

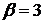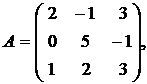
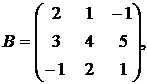
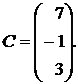
1.7. ,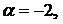

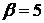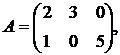
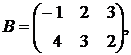
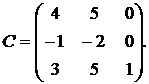
1.8. ,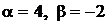

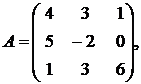
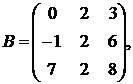
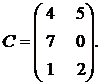
1.9. ,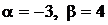

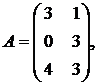
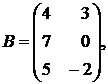
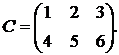
1.10. ,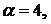

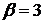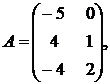
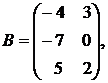
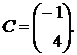
1.11. , ,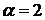

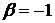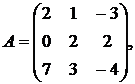
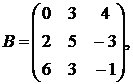
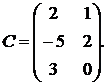
1.12. , ,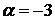

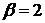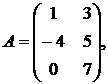
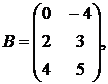
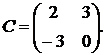
1.13. , ,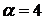

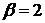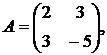
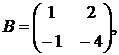
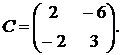
1.14. , ,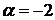

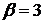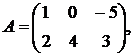
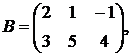
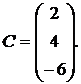
1.15. , ,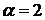

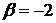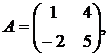
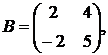
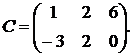
1.16. , ,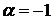

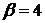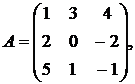
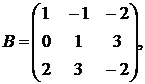
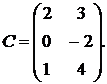
1.17. , ,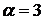

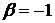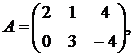
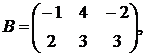
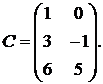
1.18. ,,,,.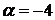

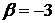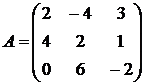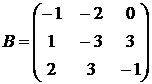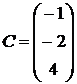1.19. , , , , .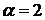

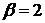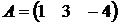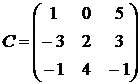1.20. , , , , .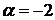

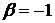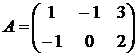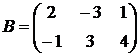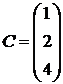1.21. , , , , .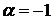

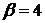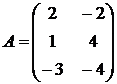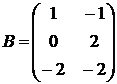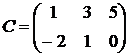1.22. , , , , .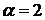

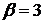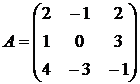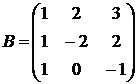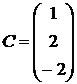1.23. , , , , .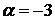

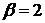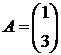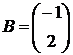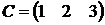1.24. , , , , .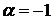

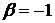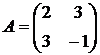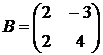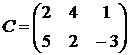1.25. , , , , .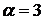

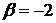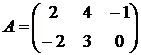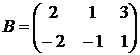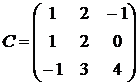1.26. , , , , .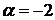

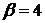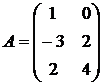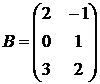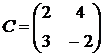1.27. , , , , .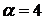

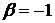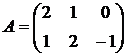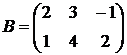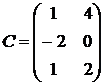1.28. , , , , .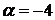

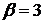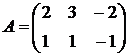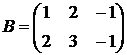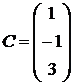1.29. , , , , .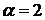

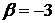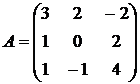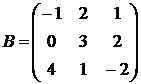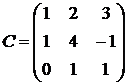1.30. , , , , .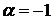

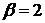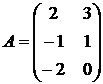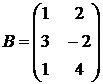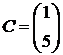№№ 2.1-2.30. Решите систему линейных уравнений по формулам Крамера и методом обратной матрицы.

2.1. 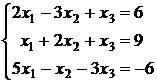; 2.2. 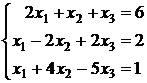; 2.3. ;

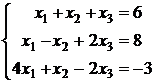2.4. 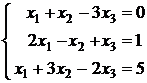; 2.5. 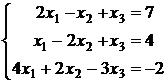; 2.6. ;

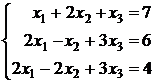2.7. 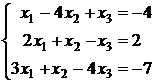; 2.8. 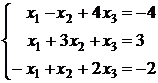; 2.9. ;

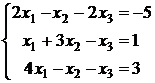2.10. 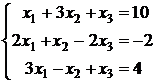; 2.11. 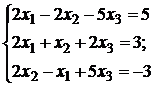2.12.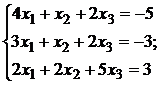

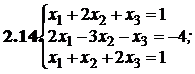
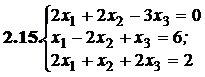
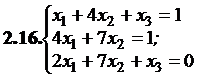
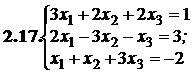
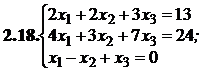
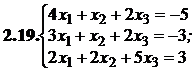
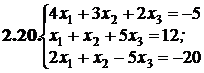
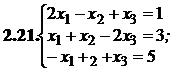
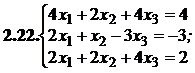
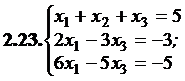
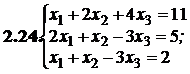
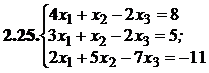
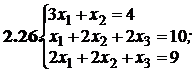
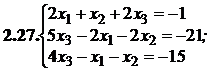
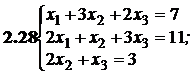
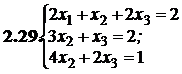
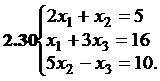
№№ 3.1-3.30.Решите систему линейных уравнений методом Жордана-Гаусса. Найдите общее, базисное и частное решения системы.

3.1. 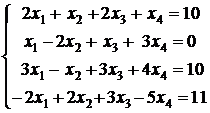; 3.2. ;

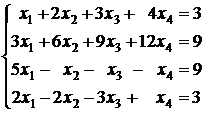3.3. 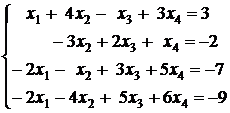; 3.4. ;

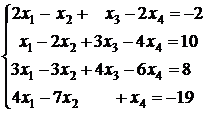3.5. 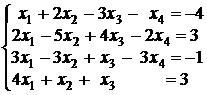; 3.6. ;

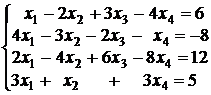3.7. 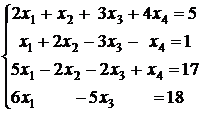; 3.8. ;

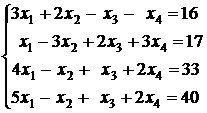3.9. 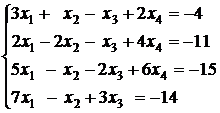; 3.10. ;

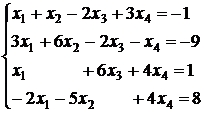3.11. 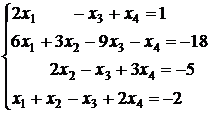; 3.12. ;

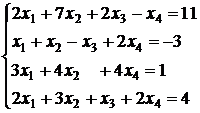3.13. 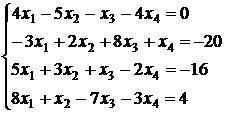; 3.14. ;

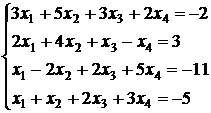3.15. 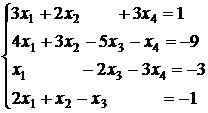; 3.16. ;

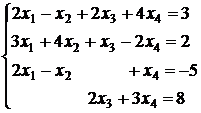3.17. 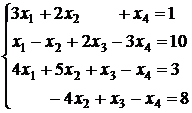; 3.18. ;

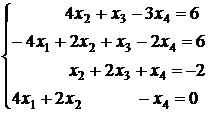3.19. 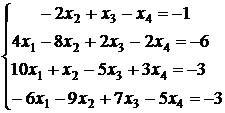; 3.20. ;

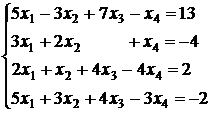3.21. 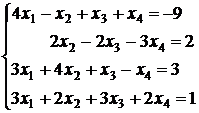; 3.22. ;

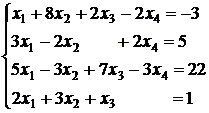3.23. 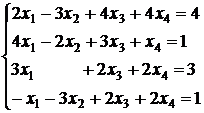; 3.24. ;

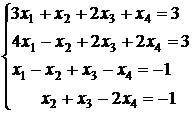3.25. 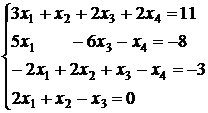; 3.26. ;

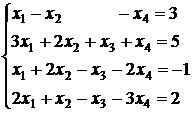3.27. 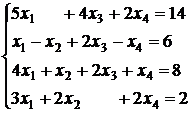; 3.28. ;

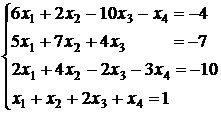3.29. 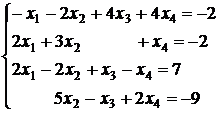; 3.30.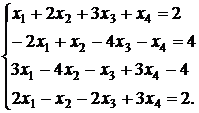

№№ 4.1-4.30. Даны координаты вершин пирамиды 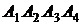. Найдите:

1) длину ребра ;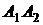

2) угол между ребрам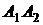и и ;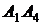

3) уравнения прямой ;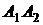

4) уравнение плоскости .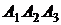

4.1. , , ;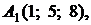

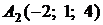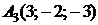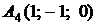4.2. , , ;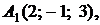

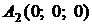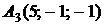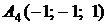4.3. , ,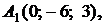

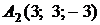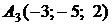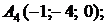
4.4. , ,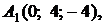

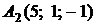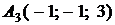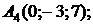
4.5. , , ;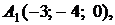

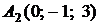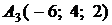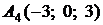4.6. , , ;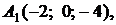

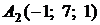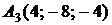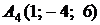4.7. , , ;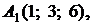

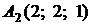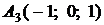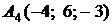4.8. , , ;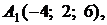

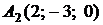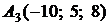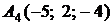4.9. , , ;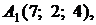

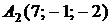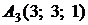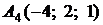4.10. , , ;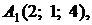

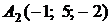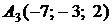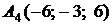4.11. ,,, ;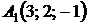

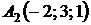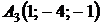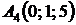4.12. , , , ;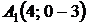

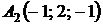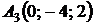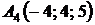4.13. , , , ;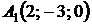

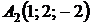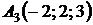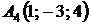4.14. , , , ;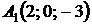

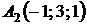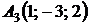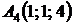4.15. , , , ;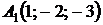

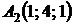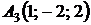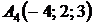4.16. , , , ;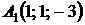

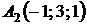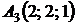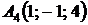4.17. , , , ;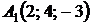

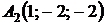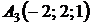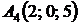4.18. , , , ;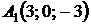

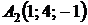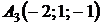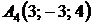4.19. , , , ;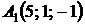

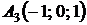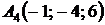4.20. , , ;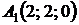

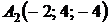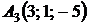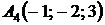4.21. , , , ;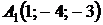

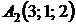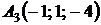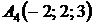4.22. , , , ;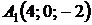

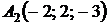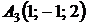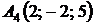4.23. , , , ;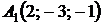

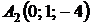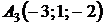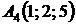4.24. , , , ;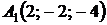

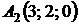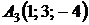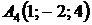4.25. , , , ;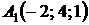

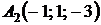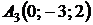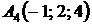4.26. , , , ;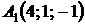

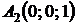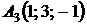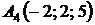4.27. , , , ;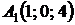

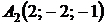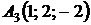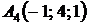4.28. , , , ;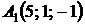

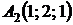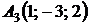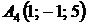4.29. , , , ;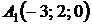

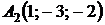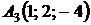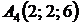4.30. , , , .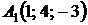

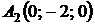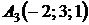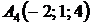№№ 5.1- 5.30 Даны координаты вершин треугольника АВС.

1. Составьте уравнения сторон треугольника.

2. Составьте систему неравенств, областью решения которой является множество

всех точек треугольника АВС.

3. Сделайте чертеж.

5.1. 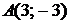, , 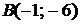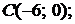5.2. ,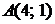

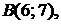
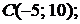
5.3. 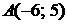, , 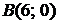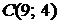; 5.4. , ,

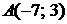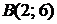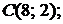
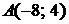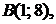
5.5. , 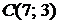; 5.6. ,

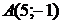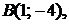
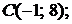
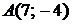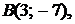
5.7. , 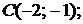5.8. ,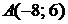

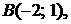
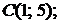
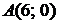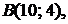
5.9. , 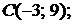5.10. ,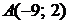

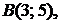
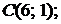
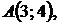
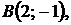
5.11. 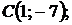5.12.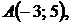

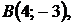
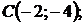
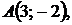
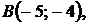
5.13. 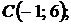5.14.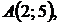

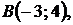
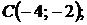
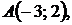
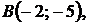
5.15. 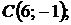5.16.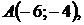

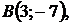
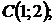
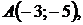
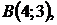
5.17. 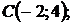5.18.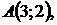

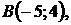
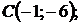
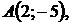
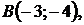
5.19. 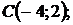5.20.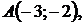

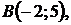
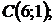
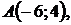
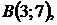
5.21. 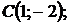5.22.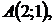

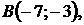
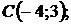
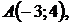
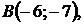
5.23. 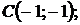5.24.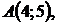

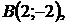
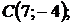
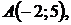
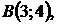
5.25. 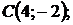5.26.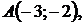

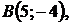
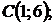
5.27. 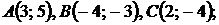5.28.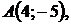

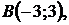
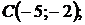
5.29. 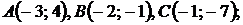5.30. .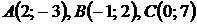

Пример решения заданий контрольной работы №1

Задание №1

Найдите 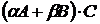, если , , ,

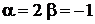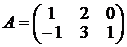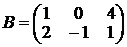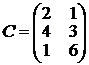
Решение:

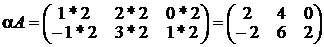
аналогично

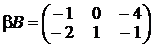
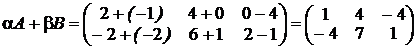
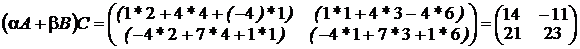
Задание №2

a)Решить систему линейных уравнений по формулам Крамера

.

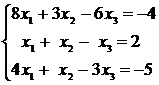Вычислим определитель системы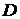

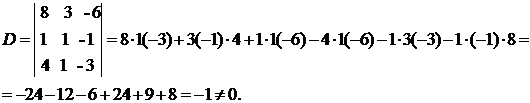
Вычислим определители D₁, D₂, D_3, заменяя в определителе D элементы первого, второго и третьего столбцов соответственно элементами столбца из свободных членов.

.

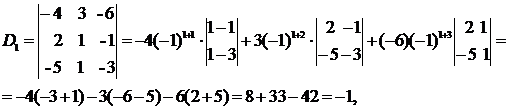
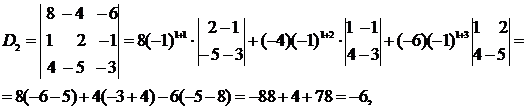
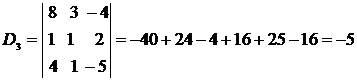Таким образом,

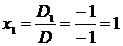, х₂= , .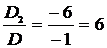

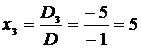Итак,

х₁=1, х₂=6, х₃=5.

b) Решить систему уравнений матричным методом:

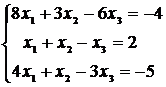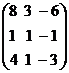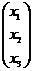. Имеем: А= , Х= , Н= .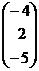

, .

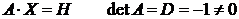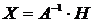Для нахождения обратной матрицы А^-1вычисляем все алгебраические дополнения элементов матрицы А:

, , ,

, , ,

, , .

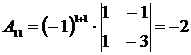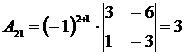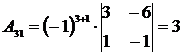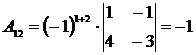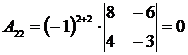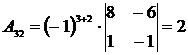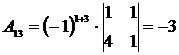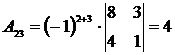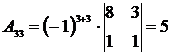Составляем обратную матрицу (1.4):

.

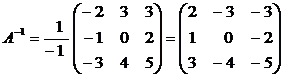Тогда

.

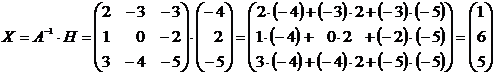Таким образом, х₁=1, х₂=6, х₃=5.

Задание №3

Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.

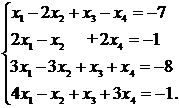
Составляем расширенную матрицу системы и проводя элементарные преобразования над строками матрицы исключаем переменные в соответствующих этой матрице системах линейных уравнений. В результате преобразований исходная матрица сводится к трапецеидальному виду. Преобразуем расширенную матрицу системы:

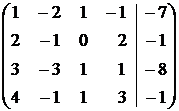
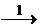
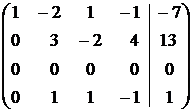
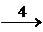
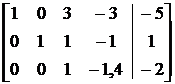
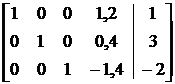
Поясним сделанные преобразования:

1. Первую строку умножим последовательно на (- 2), (-3), (-4) и прибавим ко второй, третьей и четвертой строкам соответственно.

2. Вторую строку умножаем на (-1), (-2) и прибавим к третьей и четвертой строке соответственно.

3. Поменяем местами вторую и четвертую строчку.

4. Вторую строку умножаем на 2 и на (-3) и прибавим к первой и третьей строке соответственно. Удаляем четвертую – нулевую строку.

5. Третью строку умножаем на на (-1) и на (-3) и прибавляем ко второй и первой строке соответственно.

Используя последнюю матрицу, эквивалентную исходной, получаем равносильную систему уравнений следующего вида:

х₁+ +1,2х₄= 1

х₂+ +0,4х₄ = 3

х₃+ −1,4х₄ =− 2.

Переменные х₁, х₂, х₃ назовём базисными, переменную х₄ − свободной. Полагая х₄=0, непосредственно находим базисное решение: х₁=1, х₂=3, х₃=−2.При х₄=5, получим частное решение: х₃=5, х₂=1, х₁=−5. При х₄= t, где t Î R, получим общее решение системы:

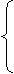х₁=1-1,2 t

х₂=3-0,4 t

х₃=-2+1,4 t.

Задание №4

Даны координаты вершин пирамиды

.

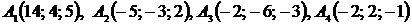Найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) уравнения прямой А₁А_2;

4) уравнение плоскости А₁А₂А₃;

1) Найдем координаты вектора :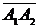

.

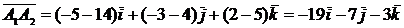Длину вектора А₁А₂ найдем по формуле:

.

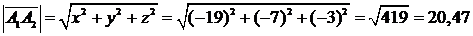2) Вектор 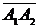уже найден. Найдем вектор :

.

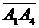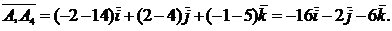
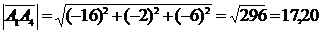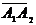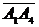Скалярное произведение векторов и найдем по формуле:

.

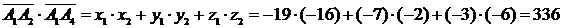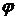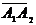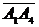Косинус угла между векторами и найдем по формуле:

, .

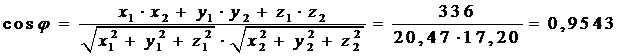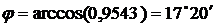3) Составим уравнения прямой А₁А₂, где 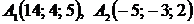. Воспользуемся уравнениями прямой, проходящей через две точк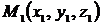и и : .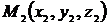

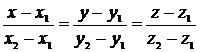Принимая за точк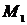и и 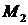соответственно 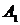и 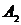, получим: .

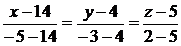Таким образом, 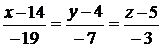— уравнения прямой .

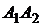4) Составим уравнение плоскости :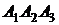

Пусть точка 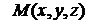принадлежит плоскости 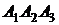. Рассмотрим векторы 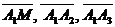и найдем их координаты:

, , .

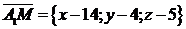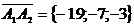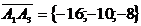Так как данные вектора компланарны, то их смешанное произведение 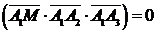. Поэтому

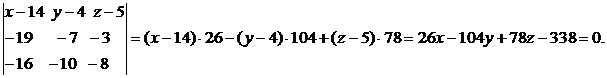
Сократив на (26), получим уравнение 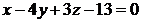. Это и есть уравнение плоскости .

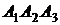Задание №5

Даны вершины треугольника : 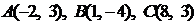. Найти:

а) уравнения сторон треугольника;

б) систему неравенств, областью решений которой является множество точек, лежащих внутри и на границе треугольника.

Сделаем чертеж

а) Составим уравнения сторон треугольника 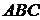. Воспользуемся уравнением: .

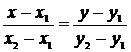Так как точки 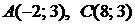принадлежат прямой АС, то

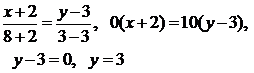
и 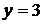— уравнение прямой АС.

Так как точки 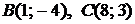принадлежат прямой ВС, то

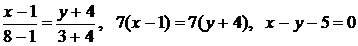, и

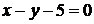— уравнение прямой ВС.

Аналогично найдем уравнение прямой АВ: 7х+3у+5=0

б) Рассмотрим уравнение 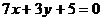. Этому уравнению удовлетворяют точки, лежащие на прямой АВ. Начало координат, т.е. точка О(0,0) лежит внутри треугольника АВС и координаты точки О(0,0) удовлетворяют неравенству 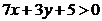, так как 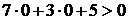. Поэтому и координаты всех точек, лежащих с той же стороны от прямой АВ, что и точка О, будут удовлетворять неравенству .

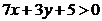Уравнению 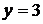удовлетворяют точки, лежащие на прямой АС. Координаты точки О(0,0) удовлетворяют неравенству 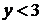, так как 0<3. Следовательно и все точки, лежащие с той же стороны от прямой АС, что и точка О будут удовлетворять неравенству .

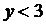Уравнению 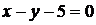удовлетворяют координаты точек, лежащих на прямой ВС. Координаты точки О(0,0) удовлетворяют неравенству 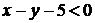, так как 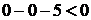. Поэтому координаты всех точек, лежащих с той же стороны от прямой ВС, что и точка О(0,0), будут удовлетворять неравенству .

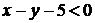Таким образом, координаты точек, лежащих как внут