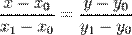Расположение прямой на плоскости. Взаимное расположение прямых
Рассмотрим две прямые (не параллельные Oy), заданные их уравнениями с угловыми коэффициентами: 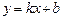 , где
, где 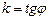 и
и 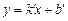 , где
, где 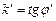 . Требуется определить угол
. Требуется определить угол 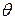 между ними (наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой,
между ними (наименьший угол, отсчитываемый против хода часовой стрелки, на который вторая прямая повернута относительно первой, 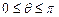 ). Этот угол
). Этот угол 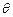 равен углу АСВ треугольника АВС. Т.к. внешний угол треугольника равен сумме внутренних, не смежных с ним, поэтому
равен углу АСВ треугольника АВС. Т.к. внешний угол треугольника равен сумме внутренних, не смежных с ним, поэтому 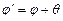 или
или 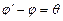 . Отсюда на основании тригонометрической формулы получаем:
. Отсюда на основании тригонометрической формулы получаем: 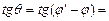
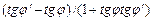 , заменяя
, заменяя 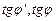 на
на 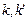 , получим:
, получим: 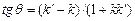 .
.
Прямые на плоскости параллельны тогда и только тогда, когда их угловые коэффициенты равны между собой.
Прямые на плоскости перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Рассмотрим прямую 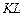 , заданную общим уравнением
, заданную общим уравнением 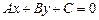 и некоторую точку
и некоторую точку 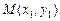 . Под расстоянием от точки
. Под расстоянием от точки 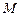 до прямой
до прямой 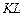 понимается длина перпендикуляра
понимается длина перпендикуляра 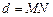
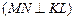 опущенного из точки
опущенного из точки 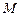 на прямую
на прямую 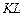 . Уравнение перпендикуляра
. Уравнение перпендикуляра 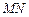 можно записать в виде:
можно записать в виде: 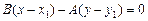 . Отсюда для основания перпендикуляра
. Отсюда для основания перпендикуляра 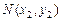 будем иметь:
будем иметь: 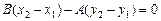 и следовательно
и следовательно 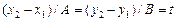 , где t – коэффициент пропорциональности. Поэтому
, где t – коэффициент пропорциональности. Поэтому 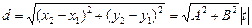 .
.
С другой стороны, учитывая, что точка 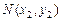 лежит на прямой KL, а
лежит на прямой KL, а 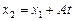 ,
, 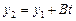 , получаем
, получаем
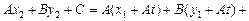
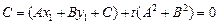 , следовательно
, следовательно 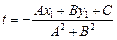 . Т.о.
. Т.о. 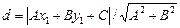
Лекция 3.2. Кривые второго порядка.
Окружность
| Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности. Уравнение окружности радиуса R с центром в точке О ( х0 , у 0 ) имеет вид: ( х – х0 ) 2 + ( у – у 0 ) 2 = R 2 . Если центр окружности совпадает с началом координат, то уравнение окружности упрощается: х 2 + у 2 = R 2 | 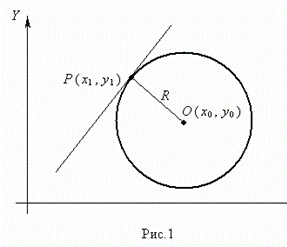 |
Пусть Р ( х1 , у 1 ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид: ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R 2 .
Условие касания прямой y = m x + k и окружности х 2 + у 2 = R 2 : k 2 / ( 1 + m 2 )= R 2 .
Эллипс
Эллипсом ( рис.1 ) называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F1 и F2 , называемых фокусами эллипса, есть величина постоянная. Уравнение эллипса ( рис.1 ) : 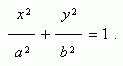 | 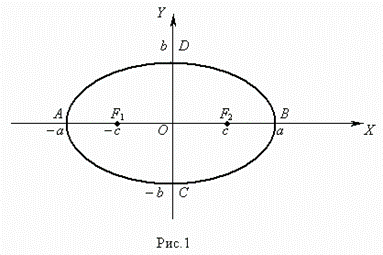 |
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса.
Отрезок F1F2 = 2 с , где 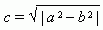 , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.
, называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.
Пусть Р ( х1 , у 1 ) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:
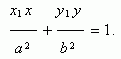
Условие касания прямой y = m x + k и эллипса х 2 / a 2 + у 2 / b 2 = 1 :
k 2 = m 2 a 2+ b 2 .
Гипербола
Гиперболой ( рис.1 ) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F1 и F2 , называемых фокусами гиперболы, есть величина постоянная. Уравнение гиперболы ( рис.1 ) 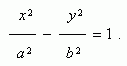 Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии. Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии. | 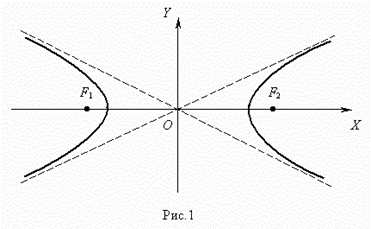 |
Отрезок F1F2 = 2 с , где 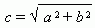 , называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осьюгиперболы. Число e = c / a , e > 1 называется эксцентриситетомгиперболы. Прямые y = ± ( b / a ) x называются асимптотами гиперболы.
, называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осьюгиперболы. Число e = c / a , e > 1 называется эксцентриситетомгиперболы. Прямые y = ± ( b / a ) x называются асимптотами гиперболы.
Пусть Р ( х1 , у 1 ) – точка гиперболы, тогда уравнение касательной к гиперболе в данной точке имеет вид:
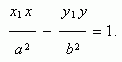
Условие касания прямой y = m x + k и гиперболы х 2 / a 2 – у 2 / b 2 = 1 :
k 2 = m 2 a 2– b 2 .
Парабола
Параболой ( рис.1 ) называется геометрическое место точек, равноудалённых от заданной точки F , называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.
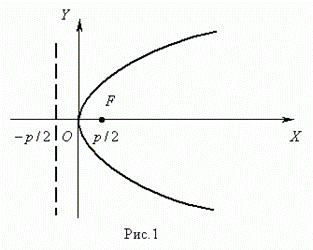
Уравнение параболы ( рис.1 ) : y 2 = 2 p x .
Здесь ось ОХ является осью симметрии параболы.
Пусть Р ( х1 , у 1 ) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид: у 1 y = p ( x + х1).
Условие касания прямой y = m x + k и параболы y 2 = 2 p x : 2 m k = p .
Плоскость
Общее уравнение плоскости: Ах + Ву + Сz + D = 0 ,
где А, B и C не равны нулю одновременно. Коэффициенты А, B и C являются координатами нормального вектора плоскости ( т.е. вектора, перпендикулярного плоскости ).
При А  0, В
0, В  0, С
0, С  0 и D
0 и D  0 получаем уравнение плоскости в отрезках на осях:
0 получаем уравнение плоскости в отрезках на осях:
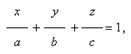
где a = – D / A , b = – D / B, c = – D / C. Эта плоскость проходит через точки ( a, 0, 0 ), ( 0, b, 0 ) и ( 0, 0, с ), т.е. отсекает на осях координат отрезки длиной a, b и c .
Уравнение плоскости, проходящей через точку ( х0 , у 0, z 0 ) и перпендикулярной вектору ( А, В, C ) : А ( х – х0) + В ( у – у 0) + С ( z – z 0) = 0 .
Условие параллельности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
AF – BE = BG – CF = AG – CE = 0 .
Условие перпендикулярности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
АE+ ВF+ СG = 0 .
Расстояние между двумя точками ( х1 , у 1, z 1 ) и( x2, y2, z2) : 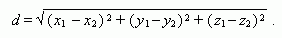
Расстояние от точки ( х0 , у 0, z 0 ) до плоскости Ах + Ву + Сz + D = 0 :
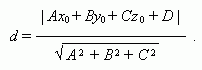
Угол 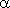 между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
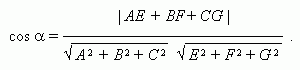
Прямая в пространстве
Уравнение прямой, проходящей через две различные точки ( х1, у 1, z 1 ) и ( х2, у 2 , z 2 ):
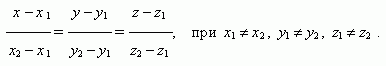
Параметрическое уравнение прямой, проходящей через точку ( х0 , у 0, z 0 ) и параллельной направляющему вектору прямой ( a, b, с ) :
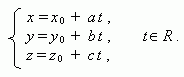
Пусть заданы две плоскости Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0, причём их нормальные векторы неколлинеарны, тогда система уравнений
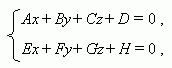
описывает прямую – линию пересечения этих плоскостей.
Пусть ( a, b, с ) и ( p, q, r ) – направляющие векторы двух прямых, тогда имеем условие параллельности прямых: aq – bp = br – cq = ar – cp = 0 ,
условие перпендикулярности прямых: ap + bq + cr = 0 ,
угол 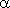 между прямыми:
между прямыми:
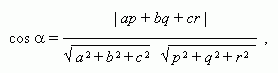
угол 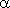 между прямой и плоскостью:
между прямой и плоскостью:
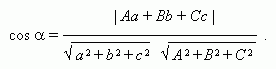
Сфера
Уравнение сферы радиуса R с центром в точке ( a, b, с )имеет вид:
( x – a ) 2 + ( y – b ) 2 + ( z – c ) 2 = R 2 .
Уравнения прямой
Направляющий вектор прямой — это любой ненулевой вектор, коллинеарный ей. Так как всякие два направляющих вектора одной прямой коллинеарны друг другу, то один из них получается из другого умножением на некоторое число, не равное нулю.
Пусть известны координаты точки 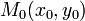 , лежащей на прямой, и направляющий вектор
, лежащей на прямой, и направляющий вектор 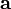 . Тогда для любой точки
. Тогда для любой точки 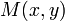 этой прямой векторы
этой прямой векторы 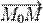 и
и 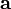 коллинеарны. Значит существует такое число
коллинеарны. Значит существует такое число 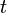 , что
, что 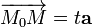 (1)
(1)
С другой стороны, всякая точка 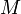 , для которой выполнено условие (1), лежит на рассматриваемой прямой. Таким образом, этому условию удовлетворяют все точки прямой и только они. Обозначим через
, для которой выполнено условие (1), лежит на рассматриваемой прямой. Таким образом, этому условию удовлетворяют все точки прямой и только они. Обозначим через 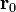 и
и 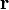 радиусы-векторы точек
радиусы-векторы точек 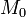 и
и 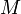 соответственно. Тогда
соответственно. Тогда 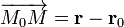 и уравнение принимает вид
и уравнение принимает вид 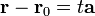 или
или 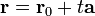 (2)
(2)
Уравнение (2) называют векторным уравнением прямой.
Если направляющий вектор имеет координаты 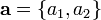 , то вместо равенства векторов можно записать равенство их координат:
, то вместо равенства векторов можно записать равенство их координат: 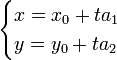 (3)
(3)
Это параметрическое уравнение прямой, проходящей через точку 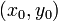 с направляющим вектором
с направляющим вектором 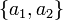 .
.
Исключая из параметрического уравнения параметр 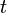 , получаем каноническое уравнение прямой:
, получаем каноническое уравнение прямой: 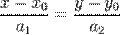 (4)
(4)
Если, например, 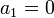 , то данное уравнение переписывают в виде
, то данное уравнение переписывают в виде 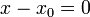 .
.
Придем уравнение (4) к общему знаменателю: 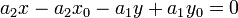
Обозначим 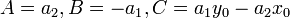 , запишем в виде
, запишем в виде 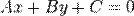 (5)
(5)
Это общее уравнение прямой на плоскости.
Поскольку вектор 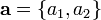 — ненулевой, то хотя бы один из коэффициентов
— ненулевой, то хотя бы один из коэффициентов 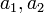 отличен от нуля. Значит левая часть уравнения (5) — многочлен первой степени от неизвестных
отличен от нуля. Значит левая часть уравнения (5) — многочлен первой степени от неизвестных 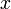 и
и 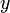 .
.
Теорема. На плоскости прямые и только прямые описываются уравнениями первой степени.
Доказательство. Прямая — уравнение первой степени. Возьмем частное решение 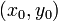 уравнения (5) и рассмотрим прямую
уравнения (5) и рассмотрим прямую 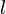 , проходящую через точку
, проходящую через точку 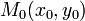 , с направляющим вектором
, с направляющим вектором 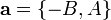 . Возьмем теперь произвольную точку
. Возьмем теперь произвольную точку 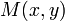 на прямой
на прямой 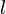 и покажем, что ее координаты удовлетворяют уравнению (5). Рассмотрим равенство
и покажем, что ее координаты удовлетворяют уравнению (5). Рассмотрим равенство 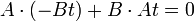 Согласно (1) существует такое число
Согласно (1) существует такое число 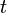 , что
, что 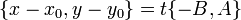
Отсюда 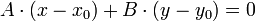 или
или 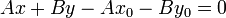 (∗)
(∗)
Поскольку 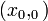 — решение уравнения (5), то
— решение уравнения (5), то 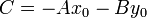 . Значит, равенство (∗) совпадает с равенством (5), то есть координаты всякой точки
. Значит, равенство (∗) совпадает с равенством (5), то есть координаты всякой точки 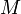 , принадлежащей
, принадлежащей 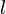 , удовлетворяют уравнению (5).
, удовлетворяют уравнению (5).
Уравнение первой степени — прямая. Пусть точка 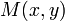 удовлетворяет уравнению (5). Тогда из того, что точка
удовлетворяет уравнению (5). Тогда из того, что точка 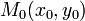 также удовлетворяет этому условию, следует
также удовлетворяет этому условию, следует
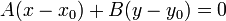 или
или 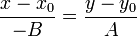 Значит, векторы
Значит, векторы 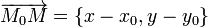 и
и 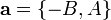 пропорциональны. Следовательно, согласно (1) точка
пропорциональны. Следовательно, согласно (1) точка 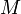 лежит на прямой.
лежит на прямой. 
Из доказательства следует, что направляющий вектор прямой, задаваемой уравнением (5), — 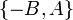 .
.
Если 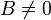 , то уравнение (5) можно переписать в виде
, то уравнение (5) можно переписать в виде 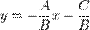 или
или 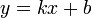 (6)
(6)
Стоит отметить, что в произвольной системе координат угловой коэффициент 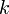 не является тангенсом угла наклона прямой к оси абсцисс, как в прямоугольной системе координат.
не является тангенсом угла наклона прямой к оси абсцисс, как в прямоугольной системе координат.
Если на прямой заданы две точки 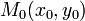 и
и 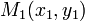 , то в качестве направляющего вектора можно взять вектор
, то в качестве направляющего вектора можно взять вектор 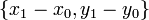 . Тогда каноническое уравнение приобретает вид
. Тогда каноническое уравнение приобретает вид