Ранг матрицы и его отыскание

Ранг матрицы, наряду с определителем квадратной матрицы, является одной из ее важнейших характеристик.

Определение. Минором порядка k матрицы А называется определитель квадратной матрицы k-го порядка, получаемой из матрицы А вычеркиванием каких-либо ее строк и столбцов.

Например, из прямоугольной матрицы размера 3 х 4, вычеркивая строки и столбцы, можно получить миноры третьего, второго и первого порядка.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.

Из сформулированного определения вытекает простейший алгоритм отыскания ранга матрицы. Для этого нужно образовать все без исключения миноры максимально возможного порядка и проверить (путем последовательного вычисления) их на отличие от нуля. Если хотя бы один из этих миноров отличен от нуля, то вычисления прекращают и заключают, что ранг данной матрицы равен порядку этого минора. Если же все такие миноры равны нулю, то образовывают миноры порядка на единицу меньшего, чем предыдущие, и проверяют их на отличие от нуля и т.д.

В общем случае, когда матрица имеет достаточно большие размеры, отыскание ее ранга описанным способом представляет собой достаточно трудоемкий и сложный (в смысле объема вычислений) процесс.

Для существенного облегчения отыскания ранга матрицы широко используются элементарные преобразо­вания строк матрицы:

1. Отбрасывание нулевой строки.

2. Умножение всех элементов строки на любое число, отличное от нуля.

3. Перестановка строк или столбцов матрицы.

4. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любое число.

Матрица, полученная из данной матрицы элементарными преобразова­ния­ми строк, называется эквивалентной данной матрице и обладает важным свойством: она имеет тот же ранг, что и данная матрица.

Кроме того, при отыскании ранга матрицы особую роль играют матрицы специального вида – ступенчатые матрицы. Примерами таких матриц являются матрицы:

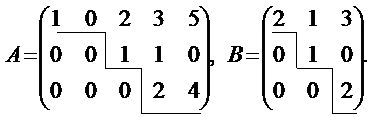
Любая ступенчатая матрица не содержит нулевых строк, а все ее ступеньки имеют в высоту одну строку, т.е. число ступенек равно числу строк такой матрицы.

Шириной ступеньки называется число элементов строки, стоящих на этой ступеньке. Например, в матрице А ширина первой (верхней) ступеньки равна 2, второй ступеньки – 1, а третьей (нижней) ступеньки – 2 элемента.

Для отыскания ранга матрицы с помощью элементарных преобразований строк переводят исходную матрицу в эквивалентную ей ступенчатую матрицу, ранг которой (равный рангу исходной матрицы!) определяется количеством ступенек (строк) в ней. Такой перевод обычно осуществляют с помощью алгоритма Гаусса.

Алгоритм Гаусса (пошаговый)

Шаг 1. Если элемент а₁₁ исходной матрицы равен нулю, т.е. а₁₁= 0, то перестановкой строк или столбцов матрицы добиваются того, чтобы элемент а₁₁ полученной матрицы был отличен от нуля.

Шаг 2. Сложением первой строки (в ней а₁₁ ≠ 0), умноженной на под­ходящие (различные для различных строк) множители, с другими строками до­биваются того, чтобы все элементы первого столбца матрицы, стоящие ниже элемента а₁₁ ≠ 0, т.е. элементы а₂₁, а₃₁, … были бы равны нулю.

Шаг 3. Теперь, либо уже получена ступенчатая матрица, либо в строках со второй по m-ую имеется по крайней мере один ненулевой элемент, который при помощи перестановки строк или столбцов (кроме первой строки и первого столбца) может быть поставлен на второе по порядку место в главной диагона­ли, т.е. на место элемента а₂₂. После этого снова выполняют операции, аналогичные шагу 2, но сложе­ние осуществляют уже со второй строкой, и в результате получают, что все эле­менты второго столбца, стоящие ниже элемента а₂₂ равны нулю и т.д. и т.д.

Аналогичные перечисленным операции применяются и к последующим строкам матрицы, а сам процесс продолжают до тех пор, пока не получат иско­мую, ступенчатую матрицу. Если в процессе выполнения таких операций на каком-то шаге получается нулевая строка, то ее вычеркивают.

ПРИМЕР: Найти ранг матрицы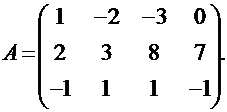

Решение. Убедившись, что для данной матрицы элемент а₁₁ = 1 ≠ 0, сразу переходим к шагу 2. Умножив первую строку матрицы на число (- 2), сло­жив ее со второй строкой и записав результат во вторую строку, а также сложив первую строку матрицы с третьей строкой и записав результат в третью строку, получим матрицу вида:

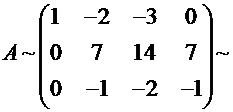
Убедившись, что в полученной после 2 шага матрице элемент а₂₂ = 7 ≠ 0, переходим к реализации шага 3, для чего умножим вторую строку этой матрицы на число 1/7 и сложим ее с третьей строкой, в результате полу­чим:

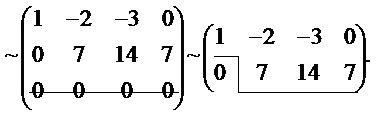
У полученной ступенчатой матрицы третья, нулевая строка может быть вычеркнута без изменения ранга этой матрицы. Оставшаяся матрица имеет раз­мер 2 ´ 4 и также является ступенчатой. Очевидно, что полученная ступенчатая матрица имеет две ступеньки (две строки), а, следовательно, ранг ее равен 2 и, следовательно, ранг исходной матрицы также равен 2.

Рекомендуемая литература по теме 1:[1 – 3].