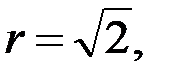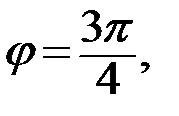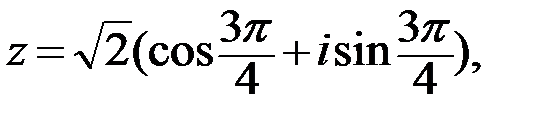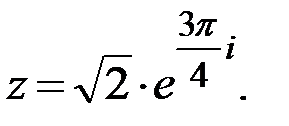Тема 6. функции нескольких переменных
Задание 1. Исследовать функцию на экстремум.
1. 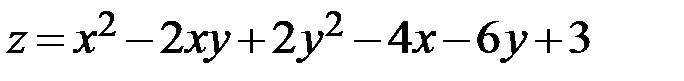 2
2
2. 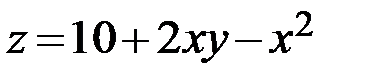
3. 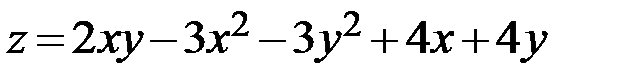
4. 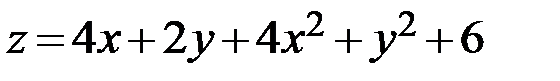
5. 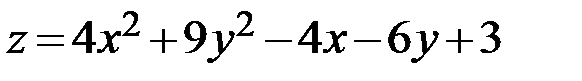
6. 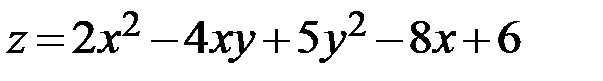
7. 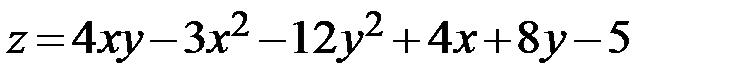
8. 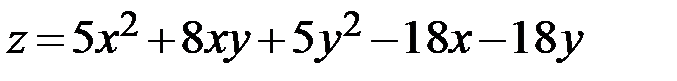
9. 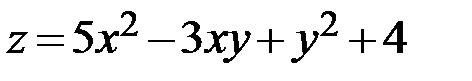
10. 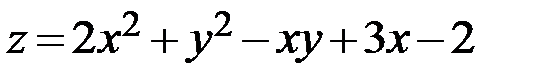
11. 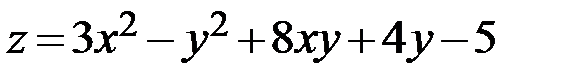
12. 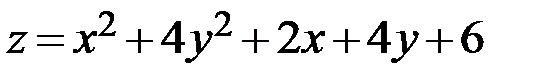
13. 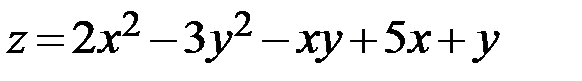
14. 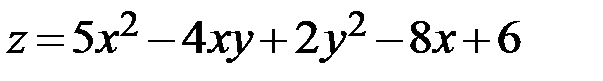
15. 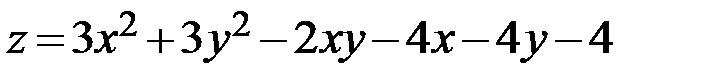
16. 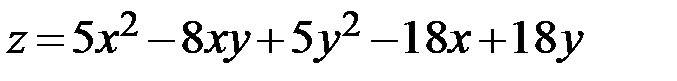
17. 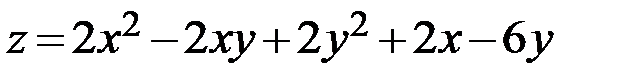
18. 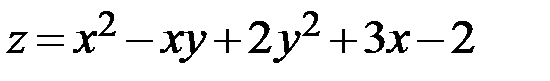
19. 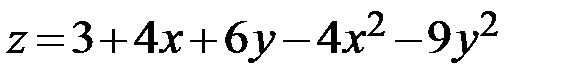
20. 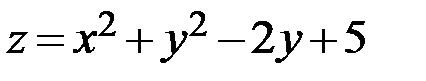
21. 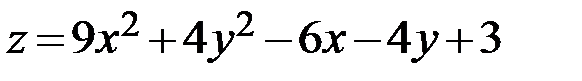
22. 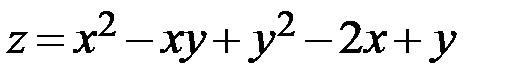
23. 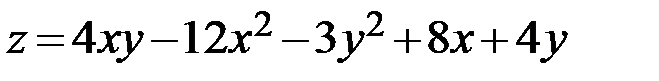
24. 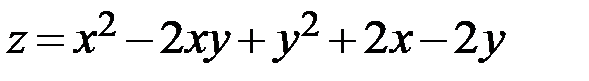
25. 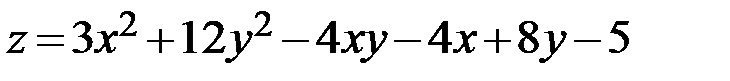
26. 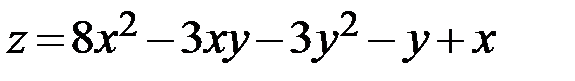
27. 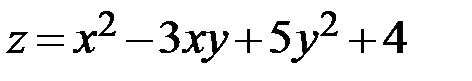
28. 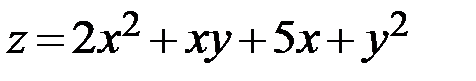
29. 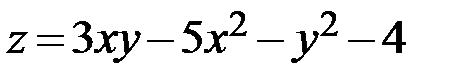
30. 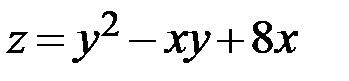
31. 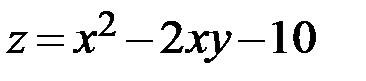
32. 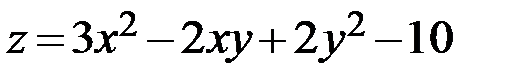
Пример. 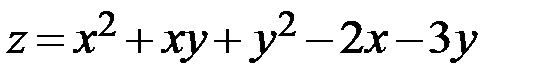 .
.
Решение. Находим частные производные первого порядка: 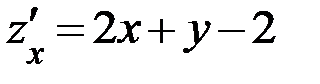 ,
, 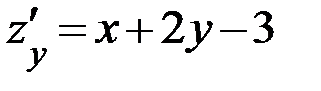 . Находим точки возможного экстремума, для этого применяем необходимое условие экстремума, то есть решаем систему уравнений:
. Находим точки возможного экстремума, для этого применяем необходимое условие экстремума, то есть решаем систему уравнений: 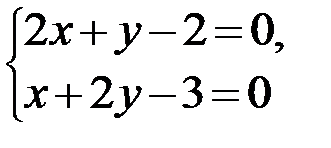 , откуда:
, откуда: 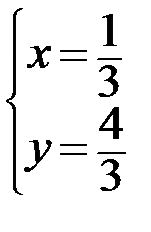 . Таким образом, точка
. Таким образом, точка 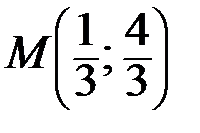 – это точка, в которой может быть экстремум функции.
– это точка, в которой может быть экстремум функции.
Далее выясним, существует ли в полученной точке экстремум. Для этого проверим достаточное условие экстремума. Находим: 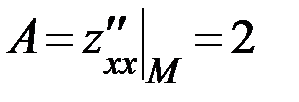 ,
, 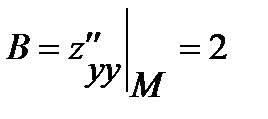 и
и 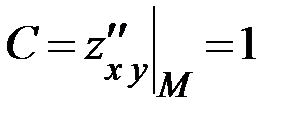 . Составляем определитель
. Составляем определитель 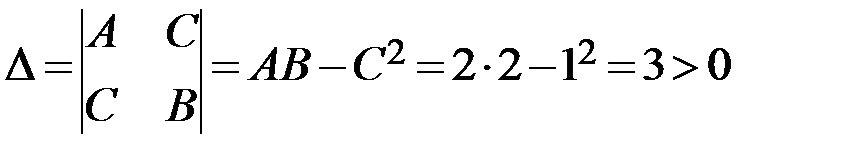 , следовательно в точке
, следовательно в точке  есть экстремум. Так как при этом
есть экстремум. Так как при этом 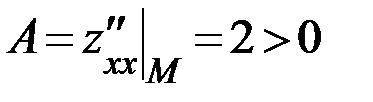 , то в точке
, то в точке 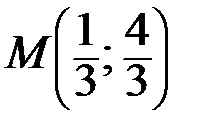 функция имеет минимум:
функция имеет минимум: 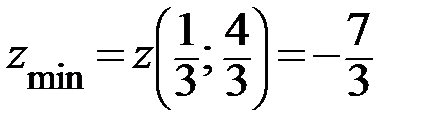 .
.
Ответ: 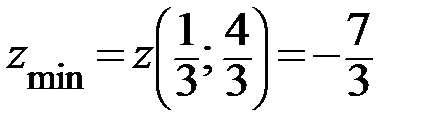 .
.
Задание 2. (Задача о площади лесовосстановления).
Имеются данные по лесовосстановлению (тыс. га) в субъектах РФ с 1990 по 2005 годы (www.sci.aha.ru/map/rus/index.htm). а) Предполагая, что между площадью S лесовосстановления и временем t существует линейная зависимость вида 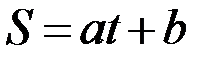 , найти значения параметров a и b методом наименьших квадратов; б) сравнить полученную зависимость с квадратичной
, найти значения параметров a и b методом наименьших квадратов; б) сравнить полученную зависимость с квадратичной 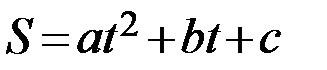 и определить, какая из них лучше соответствует экспериментальным данным; в) определить площадь лесовосстановления в 2020 году.
и определить, какая из них лучше соответствует экспериментальным данным; в) определить площадь лесовосстановления в 2020 году.
| № варианта | Субъект РФ | ||||
| Амурская область | 47,2 | 64,7 | 37,0 | 33,8 | |
| Белгородская область | 0,7 | 0,4 | 0,2 | 0,2 | |
| Брянская область | 5,1 | 4,3 | 3,4 | 3,4 | |
| Владимирская область | 8,6 | 7,3 | 4,7 | 4,7 | |
| Воронежская область | 1,3 | 1,7 | 1,6 | 1,2 | |
| Ивановская область | 6,4 | 6,1 | 3,3 | 2,6 | |
| Иркутская область | 134,2 | 114,4 | 91,3 | 91,6 | |
| Калужская область | 4,4 | 3,4 | 2,7 | 2,6 | |
| Республика Карелия | 57,0 | 55,9 | 26,9 | 27,3 | |
| Кемеровская область | 32,6 | 29,2 | 20,3 | 20,0 | |
| Кировская область | 60,7 | 38,7 | 22,7 | 24,9 | |
| Костромская область | 28,0 | 22,8 | 13,9 | 13,6 | |
| Красноярский край | 96,5 | 91,6 | 55,4 | 56,2 | |
| Курганская область | 6,3 | 5,5 | 3,8 | 2,7 | |
| Курская область | 0,8 | 0,6 | 0,5 | 0,5 | |
| Ленинградская область | 14,2 | 15,2 | |||
| Липецкая область | 0,8 | 0,6 | 0,5 | 0,5 | |
| Московская область | 5,6 | 5,5 | 4,2 | 5,1 | |
| Орловская область | 0,7 | 0,6 | 0,6 | 0,4 | |
| Пермский край | 74,6 | 50,6 | 23,4 | 25,2 | |
| Республика Бурятия | 33,3 | 20,2 | 22,8 | ||
| Ростовская область | 3,2 | 2,0 | 2,1 | 2,0 | |
| Рязанская область | 4,1 | 3,6 | 2,8 | 2,4 | |
| Свердловская область | 74,5 | 60,6 | 23,2 | 23,5 | |
| Смоленская область | 6,2 | 5,4 | 3,0 | 3,6 | |
| Тамбовская область | 2,6 | 1,9 | 1,4 | 0,8 | |
| Тверская область | 16,2 | 16,5 | 13,2 | 13,0 | |
| Томская область | 48,3 | 28,6 | 23,9 | 21,0 | |
| Тюменская область | 79,0 | 17,5 | 7,9 | 6,4 | |
| Удмуртская республика | 18,4 | 12,9 | 9,6 | 6,9 | |
| Хабаровский край | 113,5 | 105,9 | 125,1 | 125,5 | |
| Ярославская область | 6,5 | 4,1 | 3,3 | 3,9 |
| № варианта | Субъект РФ | ||||
| Амурская область | 30,7 | 30,9 | 29,6 | 33,3 | |
| Белгородская область | 0,2 | 0,3 | 0,3 | 0,4 | |
| Брянская область | 3,6 | 2,8 | 2,7 | 2,9 | |
| Владимирская область | 4,5 | 4,4 | 4,4 | 4,4 | |
| Воронежская область | 1,1 | 1,1 | 1,1 | 1,1 | |
| Ивановская область | 3,1 | 2,2 | 2,2 | 2,1 | |
| Иркутская область | 72,3 | 60,8 | 57,4 | 67,1 | |
| Калужская область | 2,7 | 2,2 | 2,2 | 2,2 | |
| Республика Карелия | 21,5 | 21,8 | 22,5 | 27,7 | |
| Кемеровская область | 12,3 | 12,0 | 13,0 | 9,7 | |
| Кировская область | 25,0 | 23,2 | 23,0 | 18,9 | |
| Костромская область | 11,2 | 10,8 | 10,5 | 10,0 | |
| Красноярский край | 48,8 | 51,1 | 50,7 | 54,1 | |
| Курганская область | 2,8 | 2,5 | 2,1 | 6,0 | |
| Курская область | 0,4 | 0,4 | 0,4 | 0,5 | |
| Ленинградская область | 16,4 | 16,8 | 17,9 | 17,4 | |
| Липецкая область | 0,3 | 0,3 | 0,4 | 0,4 | |
| Московская область | 5,2 | 5,7 | 5,9 | 6,7 | |
| Орловская область | 0,4 | 0,4 | 0,3 | 0,2 | |
| Пермский край | 24,9 | 25,3 | 25,9 | 26,4 | |
| Республика Бурятия | 23,3 | 22,9 | 22,6 | ||
| Ростовская область | 1,5 | 0,8 | 0,6 | 1,0 | |
| Рязанская область | 2,2 | 1,9 | 2,3 | 2,1 | |
| Свердловская область | 23,0 | 22,1 | 20,0 | 17,7 | |
| Смоленская область | 3,2 | 3,1 | 3,2 | 2,8 | |
| Тамбовская область | 0,8 | 0,8 | 0,6 | 0,6 | |
| Тверская область | 13,8 | 13,9 | 13,1 | 13,0 | |
| Томская область | 21,0 | 20,8 | 13,4 | 10,3 | |
| Тюменская область | 7,7 | 6,6 | 6,2 | 6,4 | |
| Удмуртская республика | 7,4 | 6,9 | 5,3 | 4,5 | |
| Хабаровский край | 101,1 | 86,4 | 85,6 | 107,2 | |
| Ярославская область | 3,9 | 3,3 | 3,2 | 2,9 |
Пример.
| Субъект РФ | |||||||
| Республика Саха (Якутия) | 49,4 | 43,2 | 45,6 | 43,6 | 43,7 | 43,4 | 40,5 |
| 43,7 |
Решение.
а) Для линейной функции 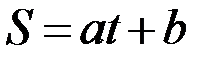 параметры a и b определяются из следующей системы уравнений:
параметры a и b определяются из следующей системы уравнений:
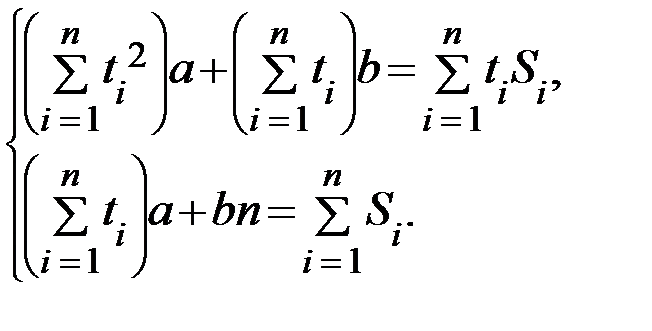
Для квадратичной функции 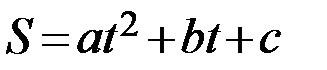 параметры a, b и с определяются из следующей системы уравнений:
параметры a, b и с определяются из следующей системы уравнений:
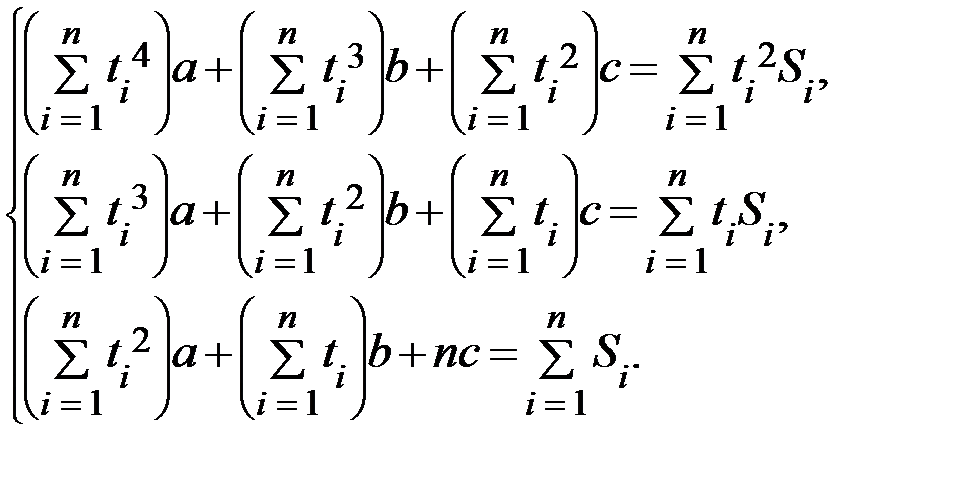
Найдём необходимые для решения суммы: 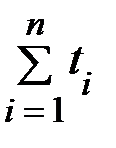 ,
, 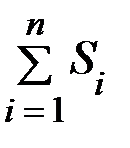 ,
, 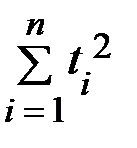 ,
, 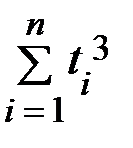 ,
, 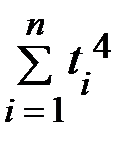 ,
, 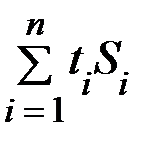 ,
, 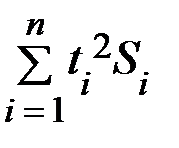 . Промежуточные вычисления представим в таблице. Для упрощения вычислений отсчёт лет начнём с 1990 года.
. Промежуточные вычисления представим в таблице. Для упрощения вычислений отсчёт лет начнём с 1990 года.
| i | 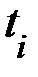 | 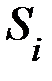 | 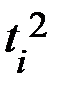 | 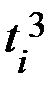 | 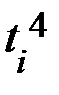 | 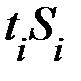 |
| 49,4 | ||||||
| 43,2 | ||||||
| 45,6 | ||||||
| 43,6 | 479,6 | |||||
| 43,7 | 524,4 | |||||
| 43,4 | 564,2 | |||||
| 40,5 | ||||||
| 43,7 | 655,5 | |||||
 | 353,1 | 3462,7 |
| i | 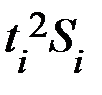 |
| 5275,6 | |
| 6292,8 | |
| 7334,6 | |
| 9832,5 | |
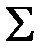 | 42313,5 |
Система уравнений для линейной зависимости имеет вид:
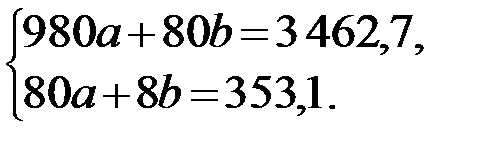
Решим систему по правилу Крамера.
Вычислим определитель системы:
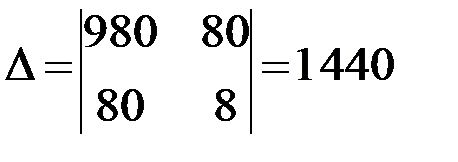 .
.
Вычислим определители 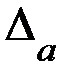 и
и 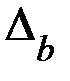 :
:
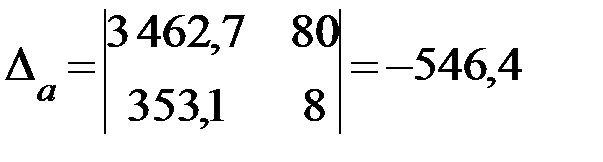
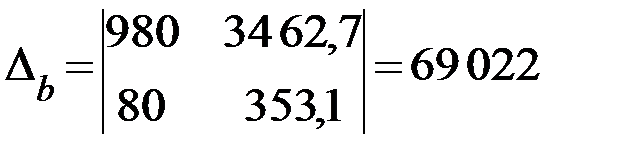 .
.
Тогда значения неизвестных параметров:
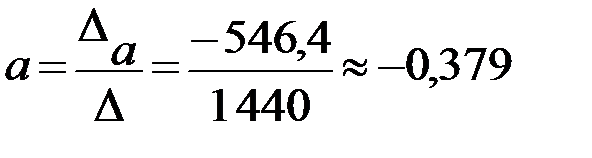
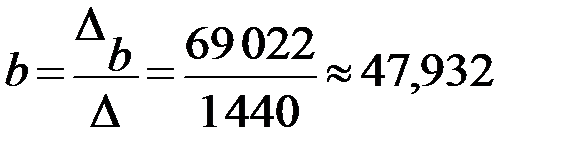 .
.
Линейная зависимость имеет следующий вид:
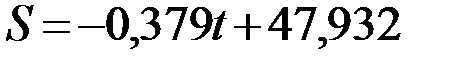 .
.
Система уравнений для квадратичной зависимости имеет вид:
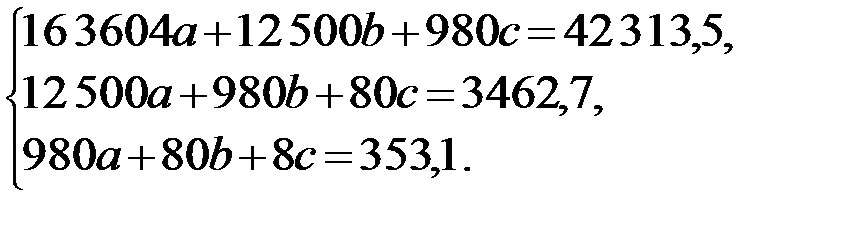
Для упрощения дальнейших вычислений разделим каждое уравнение системы на 10:
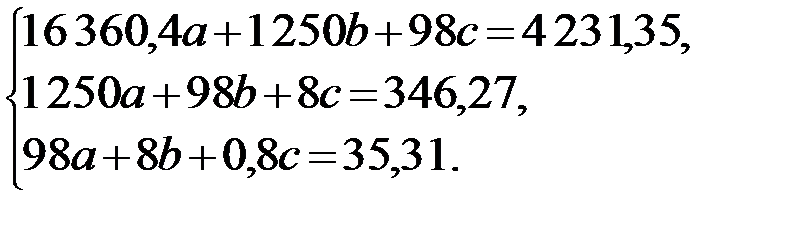
Решим систему по правилу Крамера.
Вычислим определитель системы:
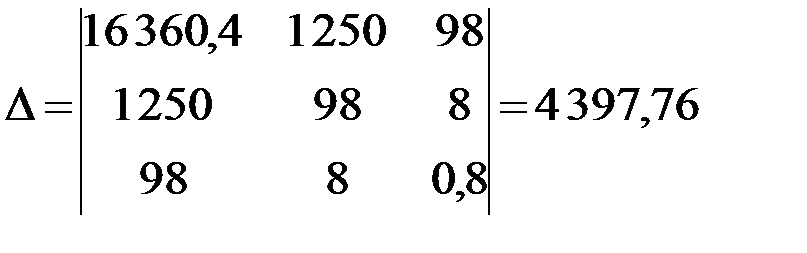 .
.
Вычислим определители 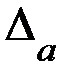 ,
, 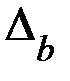 и
и 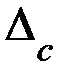 :
:

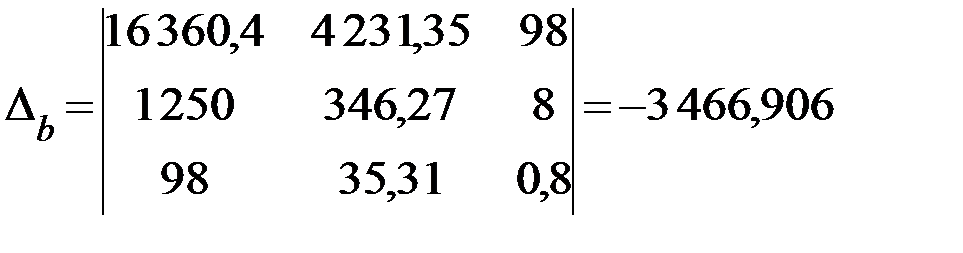

Тогда значения неизвестных параметров:
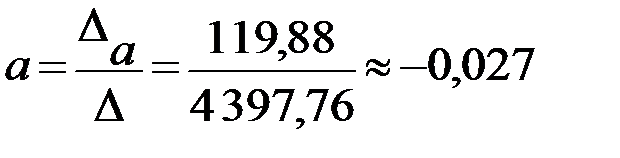
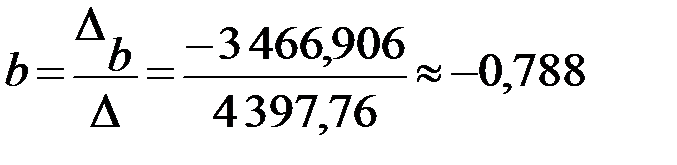
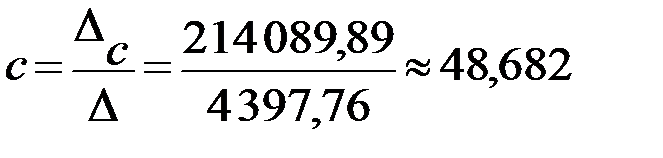 .
.
Квадратичная зависимость имеет следующий вид:
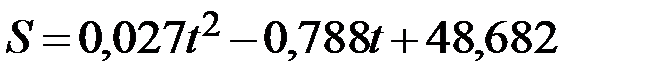 .
.
б) Для сравнения линейной и квадратичной зависимости необходимо для каждой вычислить сумму квадратов отклонений теоретических и экспериментальных значений.
Для линейной зависимости:
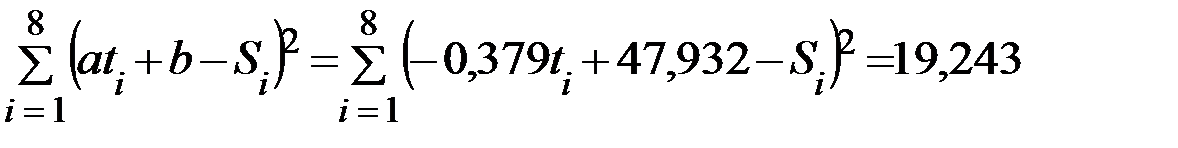 .
.
Для квадратичной зависимости:
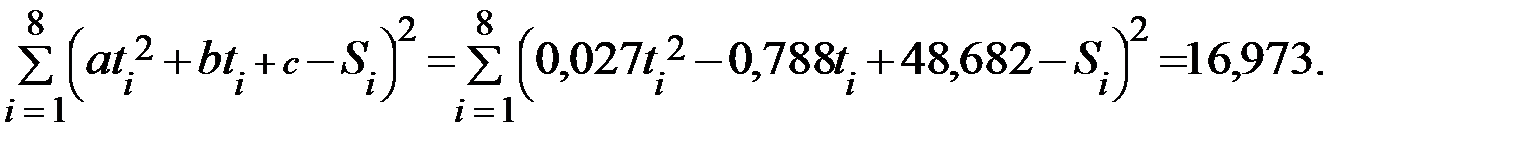 Наилучшей является та зависимость, для которой сумма квадратов отклонений меньше. В нашем примере лучшей является квадратичная зависимость.
Наилучшей является та зависимость, для которой сумма квадратов отклонений меньше. В нашем примере лучшей является квадратичная зависимость.
в) Определим площадь лесовосстановления в 2020 году.
Так как отсчёт лет начат с 1990 года, то 2020 году в нашей задаче будет соответствовать 30-й год.
Для линейной зависимости:
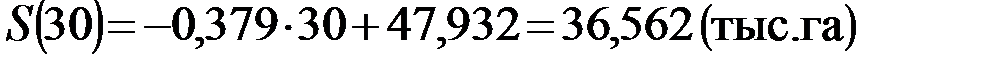 .
.
Для квадратичной зависимости:
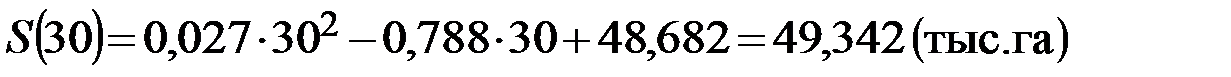 .
.
Ответ:
а) 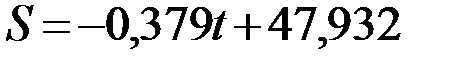 ,
, 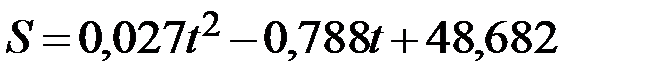 ;
;
б) лучшей является квадратичная зависимость;
в) для линейной зависимости площадь лесовосстановления в 2020 году составит 36,562 тыс. га, для квадратичной – 49,342 тыс. га.
ТЕМА 7. КОМПЛЕКСНЫЕ ЧИСЛА
Задание 1. Изобразить комплексное число на плоскости, найти его модуль и аргумент. Записать число в тригонометрической и показательной формах.
1. 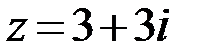 2.
2. 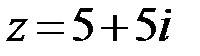 3.
3. 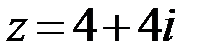
4. 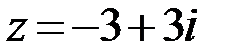 5.
5. 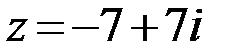 6.
6. 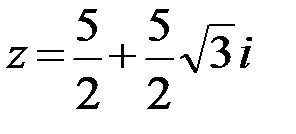
7. 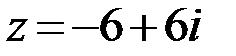 8.
8. 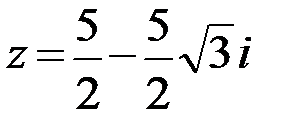 9.
9. 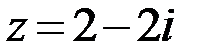
10. 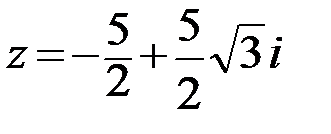 11.
11. 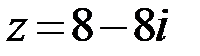 12.
12. 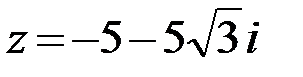
13. 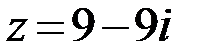 14.
14. 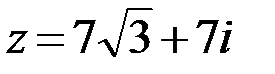 15.
15. 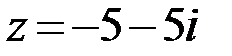
16. 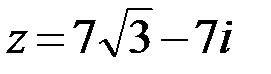 17.
17. 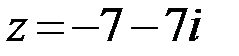 18.
18. 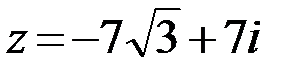
19. 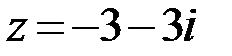 20.
20. 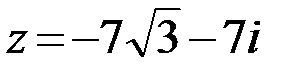 21.
21. 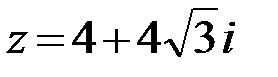
22. 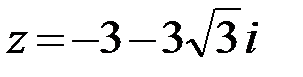 23.
23. 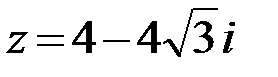 24.
24. 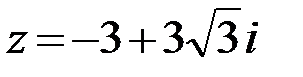
25. 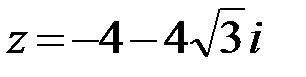 26.
26. 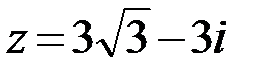 27.
27. 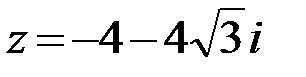
28. 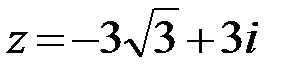 29.
29. 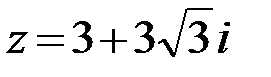 30.
30. 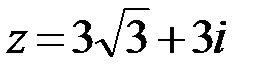
31. 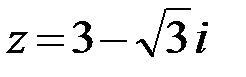 32.
32. 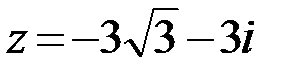
Пример. 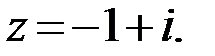
Решение. Данному числу z на комплексной плоскости соответствует точка с координатами 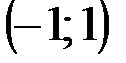 .
.
| –1 |
| z |
| x |
| y |
Пусть комплексное число записано в алгебраической форме: 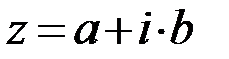 . Тогда модуль данного комплексного числа равен
. Тогда модуль данного комплексного числа равен 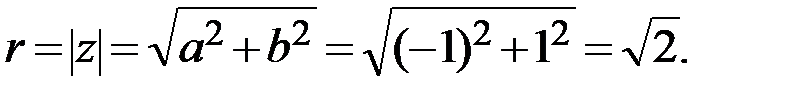 Для нахождения аргумента
Для нахождения аргумента 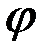 воспользуемся следующей таблицей:
воспользуемся следующей таблицей:
II четверть: 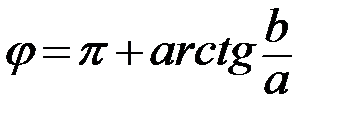 | I четверть: 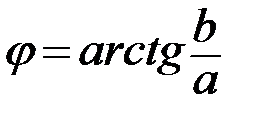 |
III четверть: 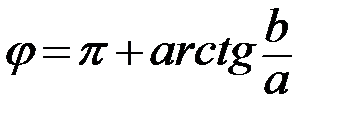 | IV четверть: 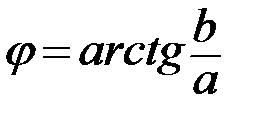 |
Тогда аргумент данного комплексного числа равен: 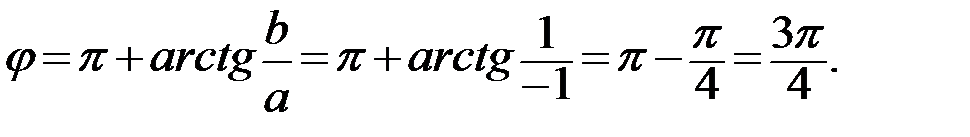
Тригонометрическая форма записи имеет вид: 
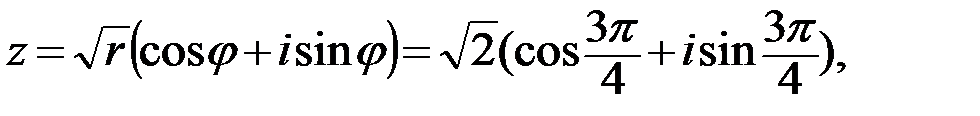
показательная форма записи имеет вид:
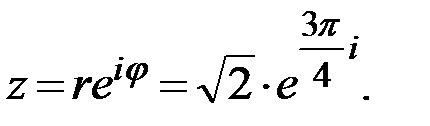
Ответ: