Определение переходной функции цепи h(t)
Переходной функции цепи называется реакция на воздействие в виде единичной ступенчатой функции. Для ее определения необходимо проанализировать переходной процесс 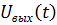 при подключении цепи к источнику постоянной ЭДС, равной 1В, при нулевых начальных условиях(рис.7).
при подключении цепи к источнику постоянной ЭДС, равной 1В, при нулевых начальных условиях(рис.7).
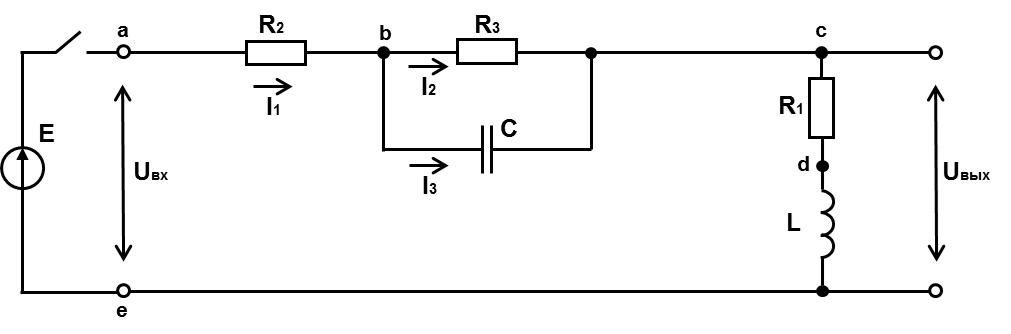
Рис.7. Схема электрической цепи с источником ЭДС
Классический метод
Классический метод предполагает представление искомой величины (в данном случае выходного напряжения) в виде суммы установившейся и свободной составляющей [2]:
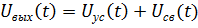
Так как необходимое напряжение 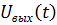 нужно рассчитать на 2-ух элементах (сопротивления
нужно рассчитать на 2-ух элементах (сопротивления 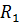 и индуктивности
и индуктивности 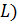 , то для расчета нужно взять ток на индуктивности и умножить на сопротивление
, то для расчета нужно взять ток на индуктивности и умножить на сопротивление 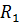 :
:
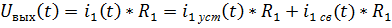
Расчет установившейся составляющей
В установившемся режиме постоянная ЭДС может вызвать только постоянные токи в цепи. Постоянный ток через емкость протекать не будет, а индуктивность представляет собой для постоянного тока короткое замыкание [2]. Поэтому ток в третьей ветви будет равеннулю 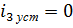 , как и напряжение на индуктивности
, как и напряжение на индуктивности 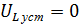 :
:
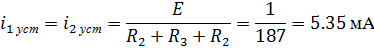
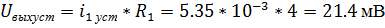
Определение общего вида свободной составляющей
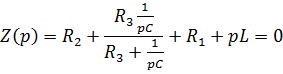
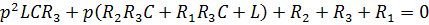
C численными значениями:
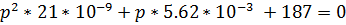
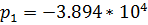 1/с
1/с
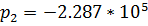 1/с
1/с
Комплексно-сопряженные корни говорят о том, что переходный процесс является апериодическим, и свободная составляющая имеет вид:
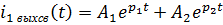 ,
,
Где 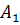 и
и 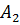 -постоянные интегрирования, которые должны быть определены из начальных условий.
-постоянные интегрирования, которые должны быть определены из начальных условий.
Общий вид результата как суммы двух составляющих:
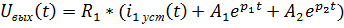
Определение начальных условий
Для вычисления постоянных интегрирования необходимо знать начальное значение искомой величины и начальное значение ее производной[2].
По 1-ому закону коммутации ток в катушке индуктивности не может измениться мгновенно, до подключения ЭДСон равен нулю. Следовательно, 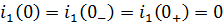
Так же по 2-ому закону коммутации напряжение на конденсаторе не может измениться мгновенно. До подключения ЭДС оно было равно нулю, следовательно, и в первый момент после подключения останется равным нулю: 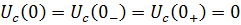
В соответствии с законами Кирхгофа составляем систему уравнений:
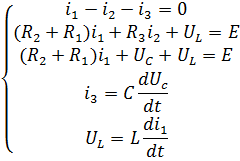
Подставив 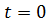 получаем:
получаем:
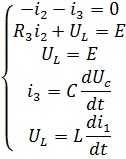
Вычисляем постоянные интегрирования
Составляем систему уравнений для тока на катушке 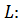
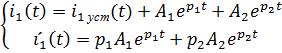
При t=0:
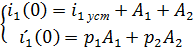
Вычислим 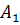 и
и 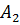 :
:
Так как по 1-ому закону коммутации ток в индуктивности не может измениться мгновенно, то при t=0 он равен нулю, выразив 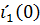 через ранее составленные уравнения Кирхгофа, составим уравнения для нахождения
через ранее составленные уравнения Кирхгофа, составим уравнения для нахождения 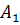 и
и 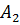 :
:
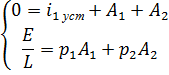
Из первого уравнения выражаем 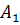 :
:
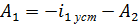
И, подставляя во второе, находим 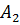 :
:
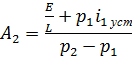
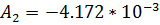
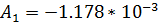
Окончательный результат:
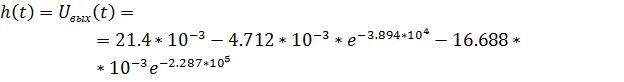
Постоянные времени цепи:
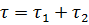
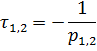
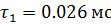
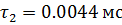
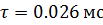
При апериодическом процессе берется максимальная из постоянных времени двух экспонент т.е. 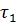 . [1]
. [1]
Операторный метод
Действия операторным методом при нулевых начальных условиях в значительной мере подобны действиям при анализе символическим методом цепей синусоидального тока при замене в выражениях сопротивлений комбинации «jω» на букву «p» [2]. Поэтому можем воспользоваться полученным выражением для комплексной частотной характеристики, записав на месте «jω» букву «p». Таким образом, мы найдем то, что называется передаточной функцией:
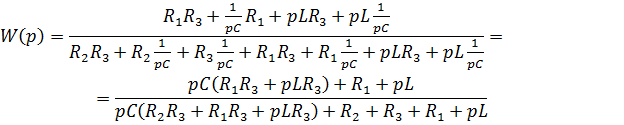
С помощью этой функции легко можно записать операторное выходное напряжение при заданном операторном входном напряжении:
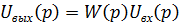
В нашем случае на входе действует постоянная ЭДС, равная 1В. Ее операторным изображением является 1/p. Значит операторным изображением переходной функции h(t) будет:
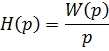
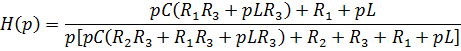
Остается найти оригинал по формуле разложения:
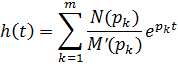
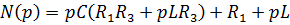
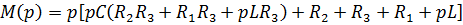
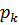 -корни многочлена
-корни многочлена 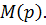
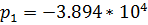 ;
; 
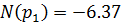
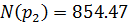
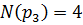
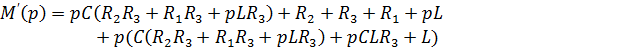
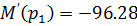
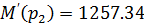
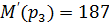
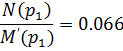
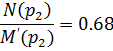
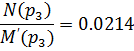
Подставляем в формулу разложения:
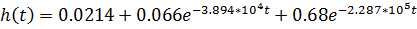
В последнем уравнении константы 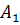 и
и 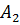 не сходятся с раннее рассчитанными константами, найденные классическим методом расчета, это свидетельствует о том, что допущена ошибка в составлении уравнений для расчета свободной составляющей тока, либо имеется ошибка в математических расчетах операторного метода.
не сходятся с раннее рассчитанными константами, найденные классическим методом расчета, это свидетельствует о том, что допущена ошибка в составлении уравнений для расчета свободной составляющей тока, либо имеется ошибка в математических расчетах операторного метода.
График переходной функции изображен на рис.8.
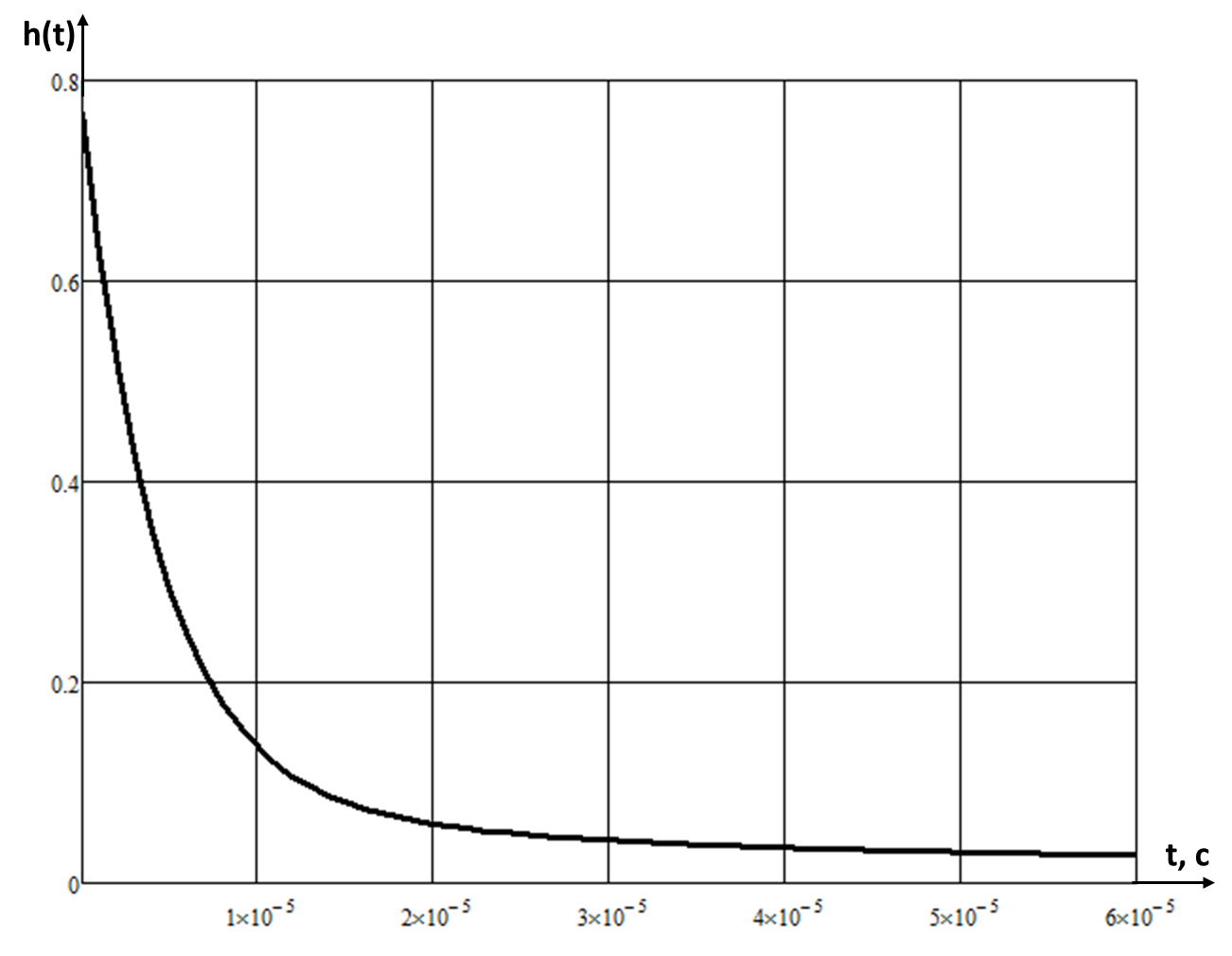
Рис.8. График переходной функции
