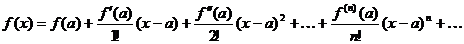Правила вычисления пределов.
Если 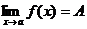 и
и 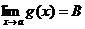 , то
, то
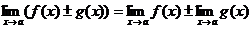 ;
;
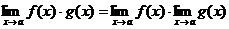 ;
;
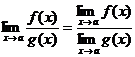 , при
, при 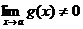 ;
;
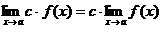 ,
, 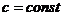 .
.
Первый замечательный предел.
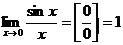 .
.
Следствия: 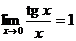 ,
, 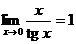
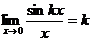 ,
, 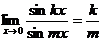
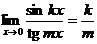 ,
, 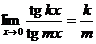
Второй замечательный предел.
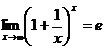 .
.
Основные неопределенности.
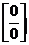 ,
, 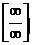 ,
, 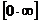 ,
, 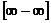 ,
, 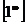 .
.
Основные эквивалентные бесконечно малые величины.
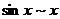 ,
, 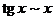 ,
, 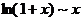 ,
, 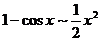 ,
, 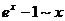 при
при 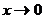 .
.
ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Правила дифференцирования.
Если 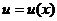 ,
, 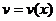 – дифференцируемые функции,
– дифференцируемые функции,
то
1. 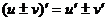
2. 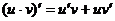
3. 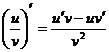
Формулы дифференцирования:
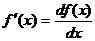
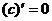 ,
, 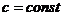
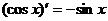
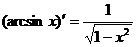
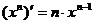 ,
, 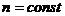
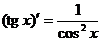
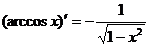
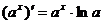 ,
, 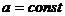
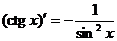
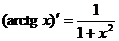
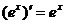
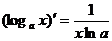
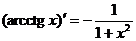
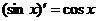
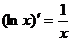
Следствие: 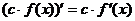 ,
, 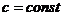
Формула Лапиталя.
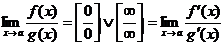
Дифференциал функции.
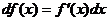
Применение дифференциального исчисления в исследовании функции 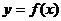
1) Если дифференцируемая функция 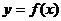 возрастает (убывает) на отрезке
возрастает (убывает) на отрезке 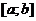 , то
, то 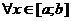
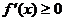
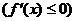 .
.
2) Если дважды дифференцируемая функция 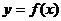 выпукла (вогнута) на отрезке
выпукла (вогнута) на отрезке 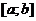 , то
, то 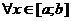
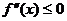
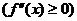 .
.
Замечание: 1. Частные производные функции нескольких переменных находятся по тем же правилам и формулам, что и для функции одной переменной, полагая, что все переменные, кроме той, по которой производится дифференцирование, являются константами.
2. Градиент функции 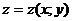 определяется по формуле:
определяется по формуле: 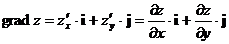
ГЛАВА X. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ.
Неопределенный интеграл.
Таблица интегралов.
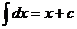
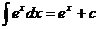
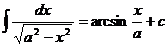
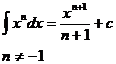
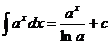
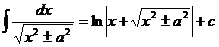
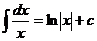
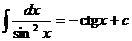
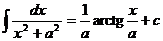
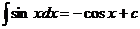
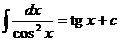
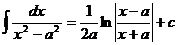
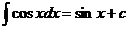
Некоторые тригонометрические формулы, применяемые при интегрировании:
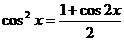 ,
, 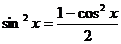 ,
, 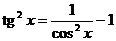 ,
, 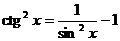
Разложение дроби на простейшие при интегрировании рациональных дробей:
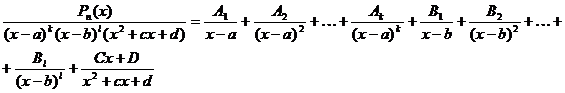
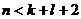 , т.е. дробь правильная
, т.е. дробь правильная
Определенный интеграл.
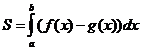
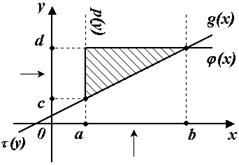
§ 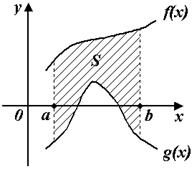 10.3. Двойной интеграл.
10.3. Двойной интеграл.
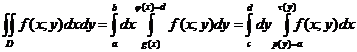
ГЛАВА XI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.
Уравнение, содержащее кроме неизвестной функции 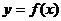 и её производные называется дифференциальным.
и её производные называется дифференциальным.
Например: 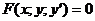 – дифференциальное уравнение 1го порядка.
– дифференциальное уравнение 1го порядка.
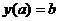 – начальное условие.
– начальное условие.
Функция 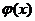 является частным решением дифференциального уравнения 1го порядка, если выполняется:
является частным решением дифференциального уравнения 1го порядка, если выполняется:
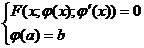
Простейшими дифференциальными уравнениями первого порядка являются уравнения с разделяющимися переменными:
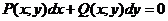 , где
, где
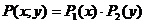 и
и
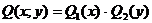
Эти уравнения решаются путем деления на 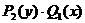 и последующего интегрирования уравнения.
и последующего интегрирования уравнения.
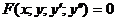 – дифференциальное уравнение 2го порядка,
– дифференциальное уравнение 2го порядка,
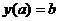 ;
; 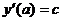 – начальные условия.
– начальные условия.
Частным случаем дифференциальных уравнений второго порядка являются линейные
неоднородные дифференциальные уравнения с постоянными коэффициентами:
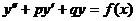
Решение 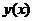 уравнений ищется в виде:
уравнений ищется в виде:
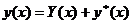 , где
, где 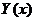 – общее решение однородного уравнения, соответствующего заданному,
– общее решение однородного уравнения, соответствующего заданному,
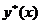 – частное решение исходного уравнения.
– частное решение исходного уравнения.
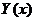 строится в зависимости от корней характеристического уравнения:
строится в зависимости от корней характеристического уравнения:
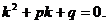

Если 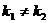 , то
, то 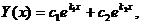
При 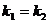 ,
, 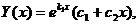
При 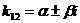 ,
, 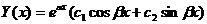
ГЛАВА XII. ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ.
Числовые ряды.
Выражение вида:
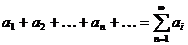 , где
, где 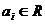
называется числовым рядом. Если 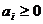
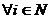 , то ряд называется знакопостоянными.
, то ряд называется знакопостоянными.
Сумма первых 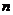 членов ряда называется частичной суммой:
членов ряда называется частичной суммой: 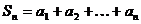 .
.
Ряд называется сходящимся, если существует 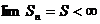 , в противном случае – расходящимся. Ряды чаще всего исследуются на сходимость с помощью признаков сходимости.
, в противном случае – расходящимся. Ряды чаще всего исследуются на сходимость с помощью признаков сходимости.
Для знакопостоянных рядов наиболее применимы следующие:
1. необходимый признак сходимости ряда:
если 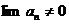 , то ряд расходится, при
, то ряд расходится, при 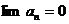 – ответ дать нельзя;
– ответ дать нельзя;
2. признак Даламбера:
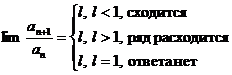
3. признаки сравнения;
4. признак Коши: Если 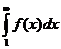 сходится, то и ряд сходится; если интеграл расходится, то и ряд расходится. Функция
сходится, то и ряд сходится; если интеграл расходится, то и ряд расходится. Функция 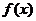 строится по формуле
строится по формуле 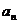 – общего члена ряда:
– общего члена ряда:
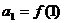 ,
, 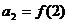 , … ,
, … , 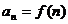 , …
, …
Замечание: 1. Ряд вида 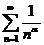 называется гармоническим. При
называется гармоническим. При 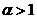 ряд сходится, при
ряд сходится, при 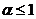 – расходится.
– расходится.
2. Ряд, составленный из членов геометрической прогрессии 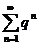 сходится при
сходится при 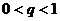 , и расходится, если
, и расходится, если 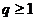 .
.
Функциональные ряды.
Ряд Тейлора для функции 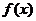 :
: