Многоканальная смо с отказами
Пусть СМО имеет не один канал, а несколько (n≥1)[6], на который поступает пуассоновский поток заявок Пвх с интенсивностью 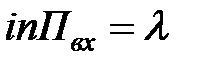 . Время Тоб обслуживания каждым каналом одной заявки распределено по показательному закону. Поток обслуживания Поб каждым каналом будет простейшим с интенсивностью
. Время Тоб обслуживания каждым каналом одной заявки распределено по показательному закону. Поток обслуживания Поб каждым каналом будет простейшим с интенсивностью 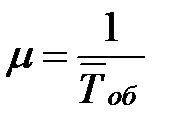 . Заявка, поступившая на вход в момент, когда все каналы заняты обслуживанием, получает отказ и покидает систему. Многоканальная СМО с отказами - классическая задача А.К. Эрланга.
. Заявка, поступившая на вход в момент, когда все каналы заняты обслуживанием, получает отказ и покидает систему. Многоканальная СМО с отказами - классическая задача А.К. Эрланга.
Запишем предельные вероятности состояний системы и показатели её эффективности в таблицы 8.4-8.5.
Таблица 8.4 - Параметры n-канальной СМО с отказами
| № п/п | Параметры | Обозначения, значения, формулы |
| 1. | Число каналов обслуживания | n≥1 |
| 2. | Интенсивность входящего простейшего потока заявок Пвх | 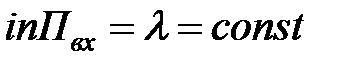 , (l не зависит от времени t) , (l не зависит от времени t) |
| 3. | Производительность каждого канала – интенсивность простейшего «потока обслуживаний» Поб (среднее число заявок, обслуживаемое одним каналом за единицу времени при непрерывной его работе без простоя) | 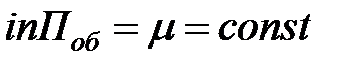 , (m не зависит от времени t) , (m не зависит от времени t) 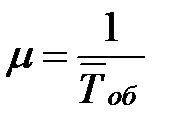 |
| 4. | Непрерывная случайная величина Тоб - время обслуживания одной заявки одним каналом, распределена по показательному закону с параметром m | 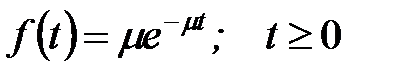 |
Таблица 8.5 - Предельные характеристики эффективности функционирования n-канальной СМО с отказами
| № п/п | Предельные характеристики | Обозначения, формулы |
| 1. | Вероятности состояний СМО рk, k=0, 1, …, n, выраженные через интенсивность входящего потока l и интенсивность потока обслуживаний m | 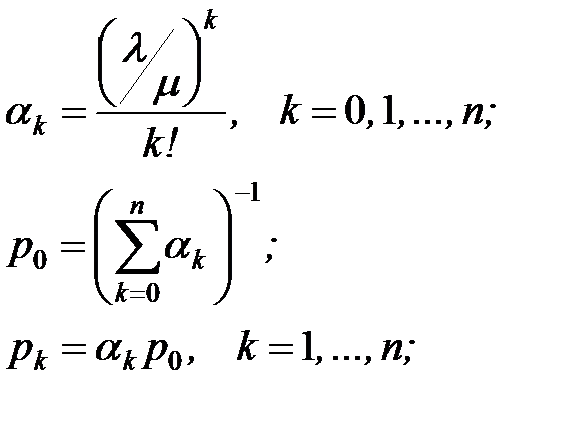 |
| 2. | Приведённая интенсивность входящего потока - трафик (показатель нагрузки СМО) | 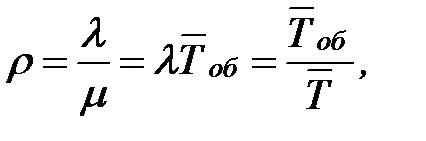 где где 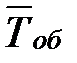 - среднее время обслуживания одной заявки одним каналом; - среднее время обслуживания одной заявки одним каналом; 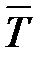 - средний интервал времени между двумя соседними заявками во входящем потоке - средний интервал времени между двумя соседними заявками во входящем потоке |
| 3. | Вероятности состояний СМО рk, k=0, 1, …, n, выраженные через трафик r | 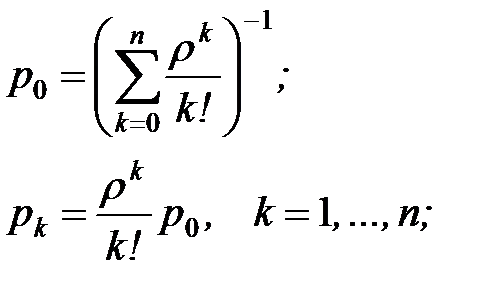 |
| 4. | Вероятности состояний СМО рk, k=0, 1, …, n, выраженные через средний интервал времени 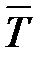 между соседними поступающими заявками, и среднее время между соседними поступающими заявками, и среднее время 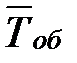 обслуживания одной заявки обслуживания одной заявки | 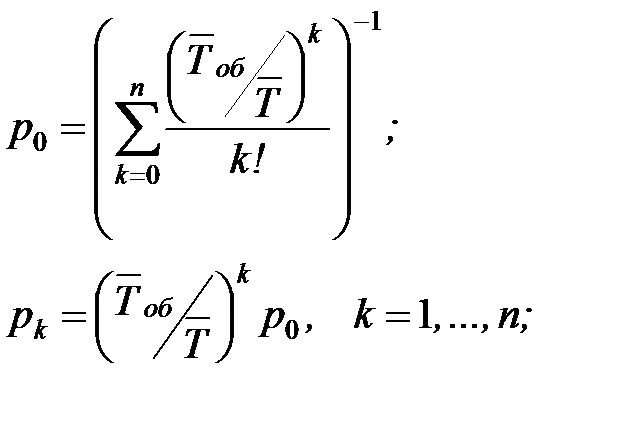 |
| 5. | Вероятность отказа ротк | 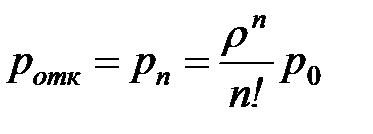 |
| 6. | Вероятность того, что поступившая заявка будет принята к обслуживанию | 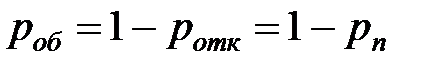 |
| 7. | Относительная пропускная способность СМО (средняя доля обслуженных заявок среди поступивших) | 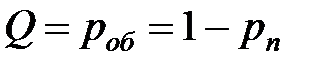 |
| 8. | Абсолютная пропускная способность СМО (среднее число обслуживаемых заявок за единицу времени) | 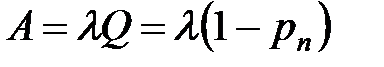 |
Продолжение таблицы 8.5
| № п/п | Предельные характеристики | Обозначения, формулы |
| 9. | Интенсивность выходящего потока обслуженных заявок | 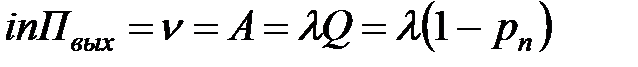 |
| 10. | Среднее число занятых каналов | 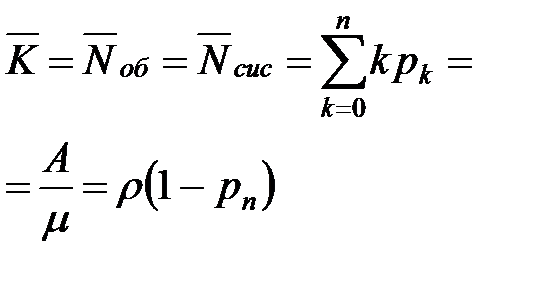 |
| 11. | Среднее время пребывания заявки в СМО (формула Литтла) | 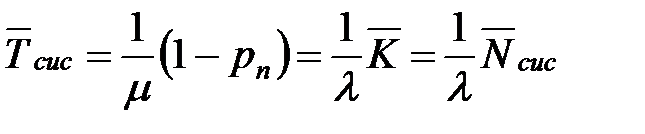 |
Задача 8.2
В мастерской бытового обслуживания работают 3 мастера. Если клиент заходит в мастерскую, когда все мастера заняты, то он уходит не ожидая обслуживания. Среднее число клиентов, обращающихся за 1 час, равно 15. Среднее время, которое затрачивает мастер на обслуживание клиента, 5 мин.
Определить основные характеристики эффективности функционирования данной мастерской в предельном режиме и:
· Вероятность того, что клиент получит отказ;
· Вероятность того, что клиент будет обслужен;
· Среднее число клиентов, обслуживаемых мастерской за час;
· Среднее число занятых мастеров.
Решение:
В условиях задачи математической моделью мастерской является многоканальная СМО с отказами, имеющая своими параметрами:
число каналов n=3;
интенсивность входящего потока 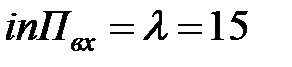 (чел./час);
(чел./час);
среднее время обслуживания 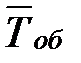 =5 мин;
=5 мин;
интенсивность потока обслуживаний 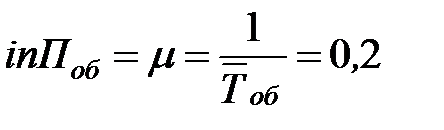 (чел./мин)=12 (чел./час);
(чел./мин)=12 (чел./час);
показатель нагрузки СМО 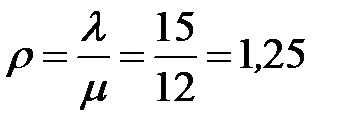 (эрланга).
(эрланга).
Вычисление предельных вероятностей состояний проведём в таблице 8.6.
· вероятность того, что все мастера свободны т.е. р0=0,2979.
· вероятность того, что только один мастер занят т.е. р1=0,3724.
· вероятность того, что два мастера заняты т.е. р2=0,2327.
· вероятность того, что все три мастера заняты т.е. р3=0,0970.
Вероятность того, что клиент получит отказ равна вероятности отказа,равна вероятности того, что заняты все три мастера, т.е. р3=0,0970.
Таблица 8.6 - Расчёт предельных вероятностей состояний
| Значения случайной величины k (число занятых мастеров) | 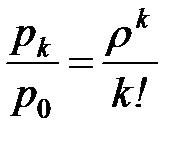 | 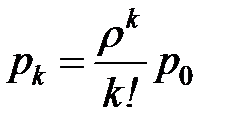 | 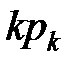 |
| 0,2979 | |||
| 1,25 | 0,3724 | 0,3724 | |
| 0,7813 | 0,2327 | 0,4655 | |
| 0,3255 | 0,0970 | 0,2909 | |
| S | 3,3568 | 1,0000 | 1,1288 |
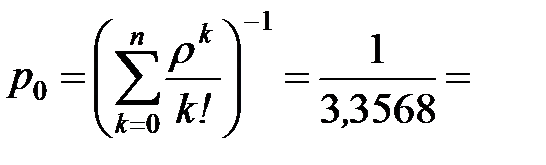 | 0,2979 |
Вычислим вероятность того, что клиент будет обслужен или вычислим относительную пропускную способность мастерской:
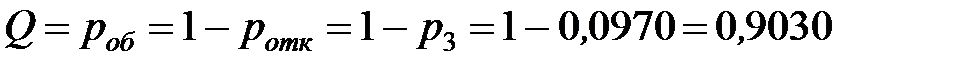 - то есть в установившемся предельном режиме из 100 человек, обратившихся в мастерскую в среднем 10 получат отказ, а 90 будут обслужены.
- то есть в установившемся предельном режиме из 100 человек, обратившихся в мастерскую в среднем 10 получат отказ, а 90 будут обслужены.
Определим предельное значение абсолютной пропускной способности:
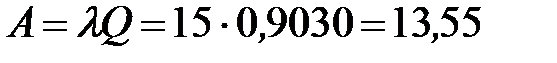 - то есть в установившемся предельном режиме среднее число клиентов, обслуживаемых за 1 час составляет 14 человек.
- то есть в установившемся предельном режиме среднее число клиентов, обслуживаемых за 1 час составляет 14 человек.
Таким образом оптимальное финансовое решение об организации мастерской должно приниматься с учётом затрат на содержание каждого мастера и потерь в доходе, связанных с необслуженными клиентами.
Контрольные вопросы
1. Кем была впервые выполнена задача исследования многоканальной СМО с отказами?
2. Графом какого процесса является размеченный граф состояний n-канальной СМО с отказами?
3. Что собой представляет приведённая интенсивность входящего потока заявок?
4. Чему равна приведённая интенсивность входящего потока заявок для многоканальной СМО с отказами?
5. Чему равна относительная пропускная способность для многоканальной СМО с отказами?
6. Чему равна абсолютная пропускная способность для многоканальной СМО с отказами?
7.Чему равна интенсивность выходящего потока обслуженных заявок для многоканальной СМО с отказами?
