Исследование функции и построение ее графика

Пусть дана функция. Для её исследования нужно:

1) Найти её область определения. Если это не слишком сложно, то полезно найти также область значений. (Однако, во многих случаях, вопрос нахождения откладывается до нахождения экстремумов функции.)

2) Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной, не является ли она периодической.

3) Найти точки пересечения графика с осями координат, что состоит в простом вычислении значения функции при условии:

С осью ОX: y=0;

С осью ОY: x=0.

Нахождение точек пересечения с осью может привести к необходимости решить сложное алгебраическое уравнение, что, быть может, удастся сделать лишь приближённо. Отыскав корни функции и точки разрыва, мы можем определить знак функции на каждом из интервалов между этими точками. Это можно сделать либо вычислив значение функции в какой-нибудь из точек интервала, либо применив метод интервалов.

4) Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения, если такие граничные точки имеются. Если функция имеет точки разрыва, то эти точки тоже проверить на наличие вертикальных асимптот функции. Найти наклонные асимптоты.

5) Найти промежутки монотонности. Для этого находят производную и решают неравенство:

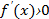. На промежутках, где это неравенство выполнено, функция возрастает. Там, где выполнено неравенство 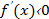, функция убывает.

Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума: там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием - локальные минимумы.

6) Нахождение интервалов выпуклости и вогнутости ведётся с помощью второй производной. Найдя 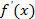, мы определяем знаки 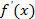на интервалах:

если 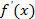›0, то кривая графика функции вогнута;

если 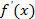‹0, то кривая графика функции выпуклая.

Заодно определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).

7) Нахождение точек пересечения графика с асимптотой и дополнительных точек. Этот пункт не носит обязательного характера, однако нахождение таких точек придаёт исследованию функции и построенному её графику законченность и полноту.

Заметим, что получающиеся в процессе исследования функции точки на осях координат и на графике полезно сразу же наносить на чертёж. Это помогает по ходу дела уяснять вид графика.

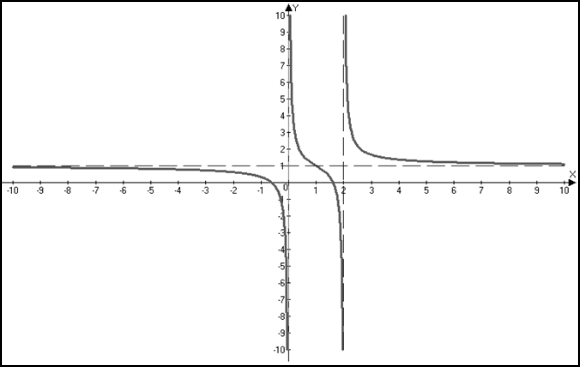
Пример 1. Исследовать функцию и построить ее график

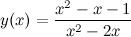
Решение. 1) Область определения функции.

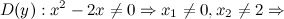
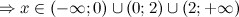
2) Четность, нечетность.

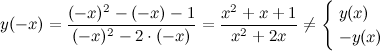
Функция общего вида.

3) Точки пересечения с осями.

а) с осью :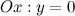

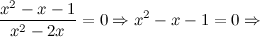
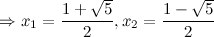
то есть точки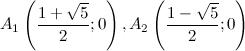

б) с осью 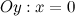: в данной точке функция неопределенна.

4) Асимптоты.

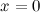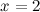а) вертикальные: прямые и - вертикальные асимптоты.

б) горизонтальные асимптоты:

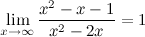
то есть прямая 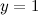- горизонтальная асимптота.

в) наклонные асимптоты :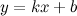

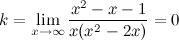
Таким образом, наклонных асимптот нет.

5) Критические точки функции, интервалы возрастания, убывания.

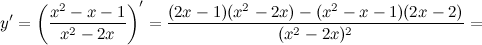
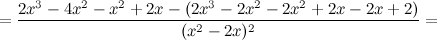
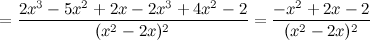
Найдем точки, в которых первая производная равна нулю или не существует: 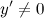для любого из области определения функции; 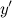не существует пр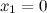и и .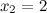

Таким образом, функция убывает на всей области существования. Точек экстремума нет.

6) Точки перегиба, интервалы выпуклости, вогнутости.

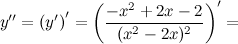
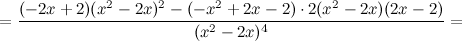
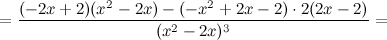
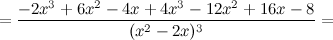
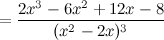
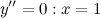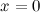Найдем точки, в которых вторая производная равна нулю или не существует: ; при и 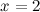вторая производная не существует.

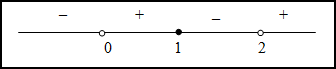
Таким образом, на промежутках 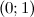и 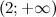функция вогнута, а на промежутках 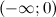и 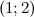- выпукла. Так как при переходе через точку 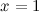вторая производная поменяла знак, то эта точка является точкой перегиба.

7) Находим дополнительные точки и строим эскиз графика.