Проверка задачи на сбалансированность

Задача является сбалансированной, т.к. количество преподавателей соответствует числу возможных видов занятий. В случае несбалансиро­ванности задачи необходимо ввести недостающее число строк или столб­цов, заполненных нулями.

Построение математической модели задачи

Пусть х_i = 1 в случае выполнения i-м преподавателем j-го вида занятий, и x_ij = 0 в случае невыполнения вида занятий. Тогда матема­тическая модель задачи примет вид – найти минимум функционала:

F = 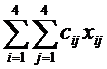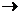min,

при следующих ограничениях:

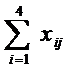= 1, j = 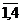, 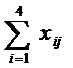= 1, i = ,

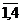x_ij 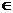{0,1}, i = 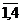, j = .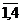

Решение задачи с помощью надстройки Поиск решения

ü подготовку рабочего листа нужно осуществить в соответствии с рисунком 4.1, где приведены и формулы для расчета.

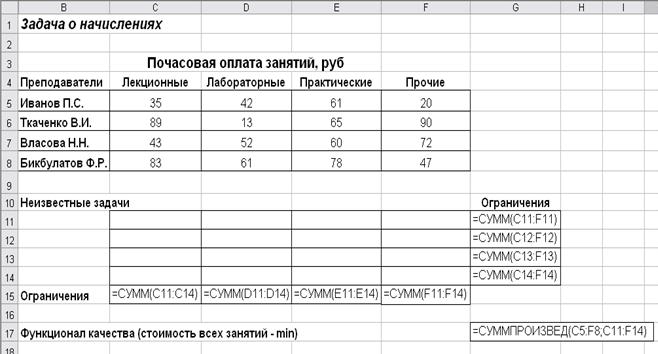
Рисунок 4.1 Вид рабочего листа для решения задачи «О начислениях»

ü ограничения в окне Поиск решения нужно установить согласно рисунку 4.2. В окне Параметры поиска решения включить флажок Ли­нейная модель.

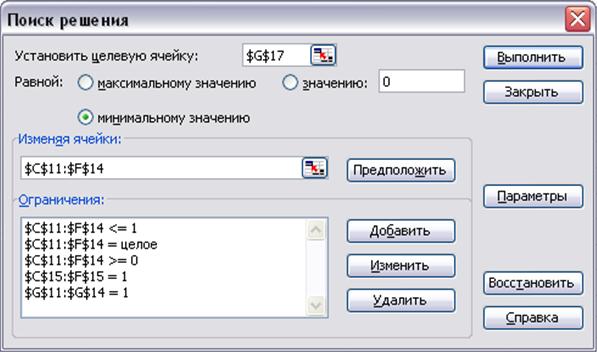
Рисунок 4.2 Установка параметров в окне Поиск решения

Пример полученного решения задачи с сохраненными параметрами модели представлен на рисунке 4.3.

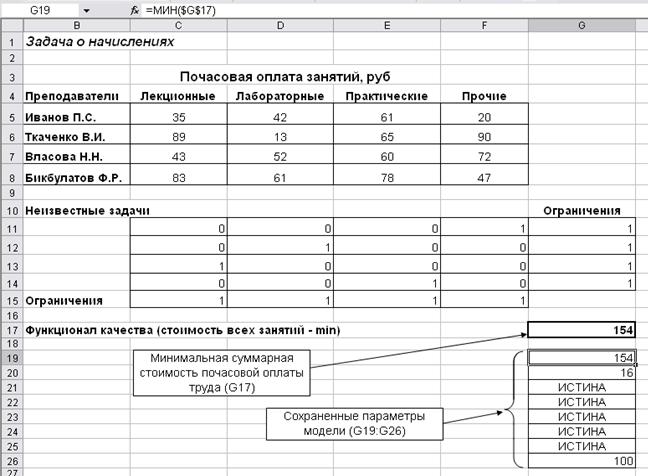
Рисунок 4.3 Решение задачи о начислениях

В таблице 4.4 показано, в каком виде надстройка Поиск решения сохраняет в ячейках параметры модели.

Таблица 4.4 Содержимое и назначение ячеек, в которых сохранены

параметры данной модели

Ячей-ка	Отобра-жаемое значение	Содержимое ячейки	Назначение
G19		=МИН($G$17)	Указана целевая ячейка и указано, что решение предназначено для достижения минимального значения
G20		=СЧЁТ($C$11:$F$14)	Указан диапазон изменяемых ячеек
G21	ИСТИНА	=$C$11:$F$14<=1	Указано первое ограничение
G22	ИСТИНА	=$C$11:$F$14= ЦЕЛОЕ($C$11:$F$14)	Указано второе ограничение
G23	ИСТИНА	=$C$11:$F$14>=0	Указано третье ограничение
G24	ИСТИНА	=$C$15:$F$15=1	Указано четвертое ограничение
G25	ИСТИНА	=$G$11:$G$14=1	Указано пятое ограничение
G26		={100:100:0,000001: 0,05:ЛОЖЬ:ЛОЖЬ: ЛОЖЬ:1:1:1:0,0001: ЛОЖЬ}	Зафиксированы параметры поиска решения, устанавливаемые в одноименном окне

В результате решения задачи в ячейках C11:F14 получен оптимальный план проведения учебных занятий. В них единицей обозначены виды занятий, распределенные между преподавателями таким образом, что каждый из них проводит занятия только одного вида, например, Власова Н.Н. читает лекции, Ткаченко В.И. проводит лабораторные работы и т.д. При этом суммарная стоимость почасовой оплаты является минимальной и составляет 154 рубля в час.

Вопросы для самоконтроля знаний

4.1 Что такое дискретное программирование?

4.2 Какие задачи относятся к дискретному программированию?

4.3 Что такое целочисленное программирование?

Лабораторная работа №5

«Решение задач нелинейного программирования методом оптимизации с помощью надстройки Поиск решения»

Цель работы:Овладеть приемами работы с надстройкой Поиск решения при решении задач по нелинейному программированию. Научиться:

ü находить оптимальное решение задачи с помощью надстройки Поиск решения при решении задач по нелинейному программированию;

ü создавать отчеты по результатам поиска решения;

ü сохранять параметры модели.

Общие сведения

Нелинейное программирование

Задача нелинейного программирования формулируется подобно задаче линейного программирования, но с учетом того, что целе­вая функция или/и хотя бы одно ограничение являются нелиней­ными. Вследствие этого задачи нелинейного программирования (НП) сложнее задач линейного программирования (ЛП). И для них не существует общего метода решения, который был бы ана­логичен симплексному методу в ЛП. Следует также заметить, что задачи нелинейного программирования включают также нели­нейные целочисленные задачи и задачи дискретного программи­рования. С учетом методов решения, задачи нелинейной оптими­зации делятся на задачи условной оптимизации (поиск экстремума функции с учетом дополнительных условий в виде ограничений и граничных условий) и задачи безусловной оптимизации (поиск экстремума функции без всяких дополнительных условий).

Для решения такого типа задач существует много различных методов. Применение того или иного метода решения зависит от типа не­линейности. Надстройка Поиск решения помогает облегчить численное решение задач нелинейного программирования.

Рассмотрим решение системы нелинейных уравнений с двумя неизвестными с помощью средства Поиск решения.

Надстройка Поиск решения позволяет находить решение систе­мы нелинейных уравнений с двумя неизвестными:

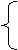f₁ (x,y) = C₁,

f₂ (x,y) = C₂, (1)

где f₁ (x,y), i=1,2 - нелинейная функция от переменных х и у, C_i , i=1,2 - произвольная постоянная.

Известно, что пара (x,y) является решением системы уравнений (1) тогда и только тогда, когда она является решением следующе­го нелинейного уравнения с двумя неизвестными:

(f₁(x,y)-C₁}² + (f₂(x,y)-C₂}² = 0 (2)

С другой стороны, решение системы (1) - это точки пересечения двух кривых: f₁(x,y} = C₁ и f₂(x,y) = C₂ на плоскости ХОY.

Из этого следует метод нахождения корней системы нелинейных уравнений:

1. Определить (хотя бы приближенно) интервал существования решения системы уравнений (1) или уравнения (2). Здесь не­обходимо учитывать вид уравнений, входящих в систему, об­ласть определения каждого их уравнений и т. п. Иногда при­меняется подбор начального приближения решения.

2. Протабулировать решение уравнения (2) по переменным x и y на выбранном интервале, либо построить графики функций f₁(x,y)=C_l и f₂(x,y)=C₂ (система (1)).

3. Локализовать предполагаемые корни системы уравнений — найти несколько минимальных значений из таблицы табули­рования корней уравнения (2), либо определить точки пересе­чения кривых, входящих в систему (1).

4. Найти корни для системы уравнений (1) с помощью надстрой­ки Поиск решения.

Содержание работы

2.1 Запустить программу MS Excel.

2.2 Создать файл аналогичный примеру 1 (Система нелинейных уравнений).

2.3 Рассмотреть все варианты нахождения оптимального решения в примере 1, установив надстройку Поиск решения.

2.4 Найти оптимальное решение с помощью надстройки Поиск решения) в заданиях для самостоятельного решения из Приложения Д. Вариант задания выбирается по указанию преподавателя.

2.5 Создать один из видов отчетов по результатам поиска решения.

2.6 Ответить на контрольные вопросы.

2.7 Составить отчет о проделанной работе, который должен содержать название работы, постановку задачи исследования, сведения о последовательности выполнения заданий с результатами и ответы на контрольные вопросы, указанные преподавателем.

3 Методика выполнения работы. Нахождение оптимального решения задачи по нелинейному программированию с помощью надстройки Поиск решения на примере системы нелинейных уравнений

Работу с надстройкой Поиск решения рассмотрим на примере системы нелинейных уравнений.

Пример 1. Решить следующую систему нелинейных уравнений:

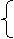(х - 1)²+(y + 1)² = 4,

5 x +4 y = 4

Легко видеть, что решением системы уравнений являются точки пересечения окружности (с радиусом 2 и центром (1,-1)) и пря­мой у=0,5-1,25х.

Данную систему можно заменить равносильным уравнением:

((х -1)² + (у +1)² - 4)² + (5х + 4у - 4)² = 0,

для которого необходимо искать решения с помощью надстройки Поиск решения.

1. Исходя из графиков уравнений, интервал локализации корней определяется в границах от -3 до 3 (рисунок 5.1). Ячейки ВЗ:В43 содержат значения X. Формулы для построения графиков:

ü в ячейке СЗ: = -1+КОРЕНЬ(4-(В3-1)^{^}2);

ü в ячейке D3: = -1-КОРЕНЬ(4-(В3-1)^{^}2);

ü в ячейке ЕЗ: = (2-5*В3)/4.

Рисунок 5.1 Графическое решение системы нелинейных уравнений

2. На рисунке 5.2 представлена табуляция равносильного уравнения на отрезке [-3; 3] с шагом 0,5.

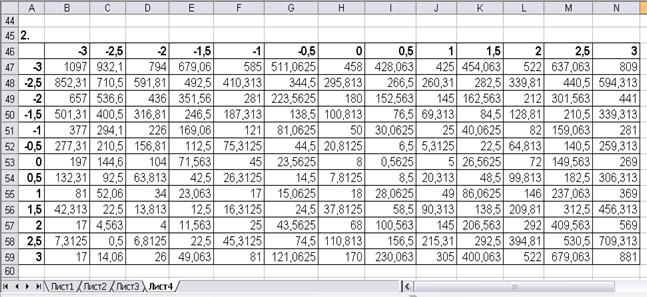
Рисунок 5.2 Табулирование функции для нахождения решения системы уравнений

3. Рисунок 5.3 – результат локализации корней равносильного уравнения:

ü ячейки А47:А59 содержат значения X на отрезке [-3; 3] с шагом 0,5;

ü ячейки B46:N46 содержат значения Y на отрезке [-3; 3] с шагом 0,5;

ü формула для ячейки В47 (копируется на диапазон B47:N59):

=(($А47-1)^{^}2+(В$46+1)^{^}2-4)^{^}2+(5*$А47+4*В$46-2)^{^}2;

ü формула для ячейки В62 (копируется на диапазон B62:N62): =МИН(В47:В60).

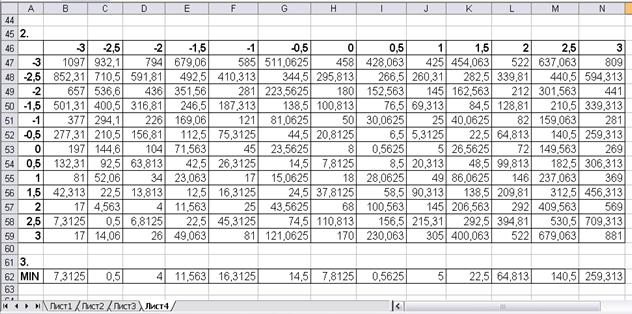
Рисунок 5.3 Локализация корней системы уравнений

Исходя из результатов вычислений, определим следующие па­ры предполагаемых корней уравнения: (-2,5; -2,5), (2; -2), (0;0,5) и (0;1).

4. Для нахождения корней равносильного уравнения (рисунок 5.4) нужно поместить пары значений для предполагаемых корней в ячейки D69:E72. В ячейку G69 ввести формулу для равно­сильного уравнения (копируется на диапазон G69:G72):

=((D69-1)^{^}2+(Е69+1)^{^}2-4)^{^}2+(5*D69+4*E69-2)^{^}2

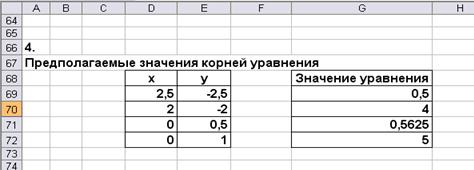
Рисунок 5.4 Подготовка листа рабочей книги для нахождения корней нелинейной системы уравнений

С помощью надстройки Поиск решения (в окне Параметры поиска решения флажок Линейная модель должен быть снят) нужно установить необходимые параметры для поиска корня равносильного уравнения (рисунок 5.5), затем вы­полнить поиск решения.

Процедуру повторить для всех имею­щихся пар корней.

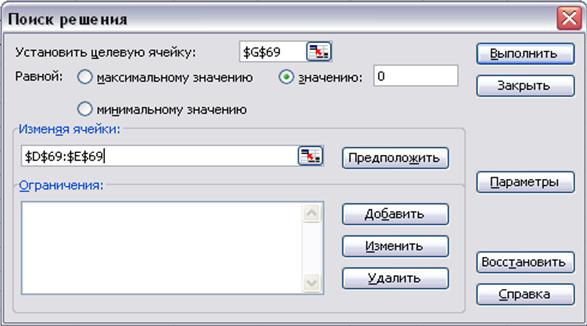
Рисунок 5.5 Ввод данных в окно Поиск решения для задачи нахождения корней системы уравнения

Результаты поиска решения (рисунок 6) позволяют сделать вывод о том, что система имеет 2 решения: (2,3675745729901; -2,45934248863711) и (-0,123564081639673; 0,654434224216163).

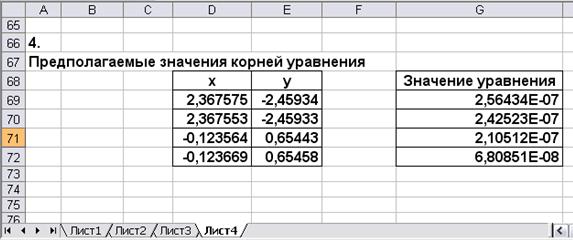
Рисунок 6 Результаты поиска решений для нелинейной системы уравнений

Вопросы для самоконтроля знаний

4.1 Что такое нелинейное программирование?

4.2 Какие задачи включают в себя задачи нелинейного программирования?

4.3 Что такое задача условной оптимизации?

4.4 На какие задачи делятся задачи нелинейной оптимизации?

4.5 Что такое задача безусловной оптимизации?

Библиографический список

1 Microsoft Excel 2000. Шаг за шагом: Практ. пособие. / Пер. с англ. – М.: Издательство ЭКОМ, 1999. – 472 с.

2 Безручко В.Т. Практикум по курсу «Информатика». Работа Windows’ 2000, Word, Excel. 2-е издание. – М.: Финансы и статистика, 2005. – 544 с.

3 Дубина А.Г., Орлова С.С., Шубина И.Ю., Хромов А.В.Excel для экономистов и менеджеров. - СПб.: Питер, 2004.-295 с.

4 Угринович Н.Д. Информатика и информационные технологии. М.:БИНОМ. Лаборатория знаний, 2003.-512 с.

5Угринович Н.Д., Босова Л.Л., Михайлова Н.И. М.:БИНОМ. Лаборатория знаний, 2004.-394 с.

6 Лавренов С. М. Excel. Сборник примеров и задач. – М.: Финансы и статистика, 2006. – 336 с.

7 Практикум по информатике / А.А. Землянский, Г.А. Кретова, Ю.Р. Стратонович, Е.А. Яшкова; Под ред. А.А. Землянского. – М.: КолосС, 2003. – 384 с.

8 Рудикова Л.В. Microsoft Excel для студента. – СПб.: БХВ-Петербург, 2005. – 368 с.

9 Серова Г.А. Учимся работать с офисными программами. MS Office 2000. - М.: Финансы и статистика, 2005. – 320 с.

10 Фандрова Л.П., Шамсутдинова Т.М. Обработка табличных данных средствами электронных таблиц для анализа задач АПК: Учеб. пособие. - Уфа: БГАУ, 2002. - 90 с.

Приложение А

Задачи для самостоятельной работы