Линейные соотношения в электрических цепях

Если в линейной электрической цепи изменяется ЭДС или сопротивление в

какой-либо ветви, то две любые величины (токи и напряжения) двух любых

ветвей связаны друг с другом линейными зависимостями вида [1, 10]

Функцию x выполняет ток или напряжение одной ветви, функцию y − ток

или напряжение другой ветви.

Доказательство.Согласно методу контурных токов, общее выражение для тока в k-ветви записывают в виде уравнения (10.2). Если в схеме изменяется только одна ЭДС то все слагаемые в уравнении (10.2), кроме слагаемого постоянны и могут быть для сокращения записи заменены некоторым слагаемым

Следовательно,

(14.1)

Аналогично, для p-ветви

(14.2)

Найдём 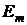из уравнения (14.2):

и подставим в выражение (14.1). Получим:

(14.3)

где

Коэффициенты и могут быть как , так и . В частном случае либо либо может быть равно нулю.

Равенство (14.3) свидетельствует о том, что при изменении ЭДС 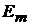токи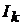

и связаны линейной зависимостью. Из теоремы компенсации известно, что

любое сопротивление можно заменить источником ЭДС. Следовательно, изме-

нение сопротивления в m-ветви эквивалентно изменению ЭДС 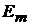. Таким об-разом, линейное соотношение между двумя любыми токами выражения (14.3) имеет место при изменении не только ЭДС но и сопротивления некоторой m-ветви.

Если обе части уравнения (14.1) умножить на сопротивление k-ветви и проделать аналогичные выкладки, то можно убедиться в том, что напряжение

k-ветви линейно связано с током в p-ветви.

Коэффициенты и из уравнения (14.3) и в других подобных выражени-

ях могут быть найдены расчётным или опытным путём.

Если в схеме одновременно изменяются ЭДС или сопротивления в каких-

либо двух ветвях, то любые три величины в этой схеме (токи, напряжения) связаны друг с другом линейным соотношением вида

Пример 25. На рис. 14.1 изображена схема, в которой выделены три ветви.

Рис. 14.1

В ветви 1 включен амперметр в ветви 2 амперметр . В ветви 3 име-

ется ключ 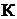и сопротивление . Если 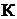разомкнут, то амперметр показы-

вает амперметр . При замкнутом ключе амперметр показывает , а амперметр . При замкнутом ключе сопротивление изменили так, что показание амперметра стало . Каково показание амперметра в этом режиме?

Решение. Выразим 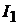через 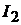. Составим уравнение для определения a и

Отсюда и . При

Пример 26.Всхеме (рис. 14.2) сопротивление 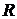изменяется от нуля до бес-

конечности. Вывести зависимость напряжения от напряжения .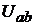

Рис. 14.2

Решение. При разомкнутой цепи и . При коротком

замыкании ветви и . Отсюда и . Следо-

вательно, .

Пример 27.На рис. 14.3, а изображена схема с сопротивлением R, изменяю-

щимся от нуля до бесконечности. Найти зависимость тока в каждой ветви от напряжения U на зажимах сопротивления R, если и .

а б

Рис. 14.3

Решение. Сначала следует найти предельные значения напряжения U и то-

ка I при коротком замыкании и холостом ходе рассматривае-

мой ветви. При ток а напряжение . Для схемы рис. 14.3, б

откуда

Так как токи

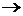
Для определения тока (см. рис.14.3, в) можно предварительно найти нап-

ряжение на зажимах параллельных ветвей по формуле:

а затем токи в ветвях:

и ток

Зависимость тока I в сопротивлении R от напряжения U на его зажимах определяется уравнением прямой

Для нахождения коэффициентов a и b следует воспользоваться режимами

холостого хода и короткого замыкания.

При напряжение а ток . При ток

напряжение и откуда

В результате получаем

Зависимость тока 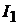в первой ветви от напряжения U определяется уравне-

ем прямой

Для того чтобы найти коэффициенты и целесообразно воспользовать-

ся и в этом случае режимами холостого хода и короткого замыкания ветви с переменным сопротивлением R.

При напряжение а ток при (см. рис. 14.3, б)

С другой стороны,

откуда

Следовательно,

Аналогично определяются токи в остальных ветвях:

Пример 28.В схеме, показанной на рис. 14.4, сопротивление изменяется в пределах от (короткое замыкание) до (размыкание ветви). Поль-

зуясь законами Кирхгофа, выразить токи и 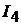через параметры схе-

мы и напряжение .

Рис. 14.4

Решение. Из уравнения непосредственно находим ток

Ток 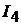определим по первому закону

Кирхгофа:

Для определения токов 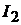и можно воспользоваться следующими урав-

нениями:

Из этих уравнений:

Ток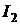и и не зависят от сопротивления и при любых его значениях

остаются неизменными.