Создание генеральной совокупности
Введение
Допустим, что изучается качество или свойство некоторого изделия (продукта) или явления в определенном технологическом (экономическом, социальном) процессе. Не умаляя общности, примем, что всего существует 1000 изделий, которые составляют «генеральную совокупность». «Не умаляя общности» означает, что с равным (для методического подхода) успехом можно принять и 10 тыс. и 10 млн. изделий.
Будем считать, что интересующее нас качество изделия определяется величиной одного из параметров (характеристик), который обозначим как признак Х.
Допустим, также, что из предшествующего опыта известно, что изучаемый параметр имеет близкое к нормальному распределение со средним значением, равным μ=60, и стандартным отклонением σ=10. Плотность распределения вероятности такого распределения задаётся формулой
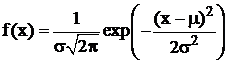
Создание генеральной совокупности
Копируем в индивидуальную рабочую папку книгу MS Excel «Шаблон» и присваиваем ей название (по фамилии студента).
Введем термин «симуляция» как понятие «моделирования», например, численного (этот термин многозначен в русском языке из-за трудности перевода англ. simulation - «моделирование»).
В качестве генеральной совокупности будем использовать несистематизированные данные, полученные в результате компьютерной симуляции 1000 наблюдений параметра.
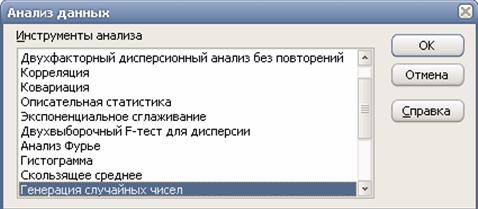
Для компьютерной симуляции нормально распределенной случайной величины (НРСВ) используем надстройку MS Excel «Сервис \ Анализ данных \ Генерация случайных чисел»:
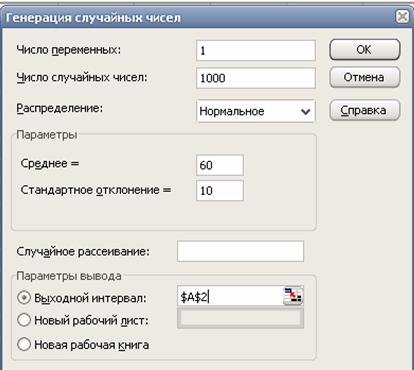
Вводим необходимые сведения по схеме на следующем рисунке и выходной интервал курсором указываем в ячейке А2 листа НРСВ.
В результате наблюдаем в столбце А тысячу двузначных случайных чисел. Последовательно, по 50 чисел, формируем здесь же «Таблицу НРСВ» и копируем ее в файл отчета. Файл отчета можно создать на основе данной инструкции, если скопировать ее и присвоить собственное наименование в MS Word.
Таблица НРСВ. Нормальная генеральная совокупность: N=1000, μ=60, σ=10
Графическое представление вариационного ряда
На листе «Графика» строим средствами MS Excel диаграммы распределения из таблицы 3.
Полигоном частот называют ломаную, отрезки которой соединяют точки (Хс;mi), где Хс - середина интервала группировки, mi - соответствующая данному интервалу частота.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников с основаниями длиной ΔХ и высотами mi.
Откладывая по оси ординат соответствующие интервалам группировки накопленные частоты Nx, получают так называемую огиву. Нормальное распределение принимает на диаграмме огивы форму S-образной кривой.
Копируем в шаблон таблицу 3 и наблюдаем эти диаграммы, которые далее переносим в файл отчета:
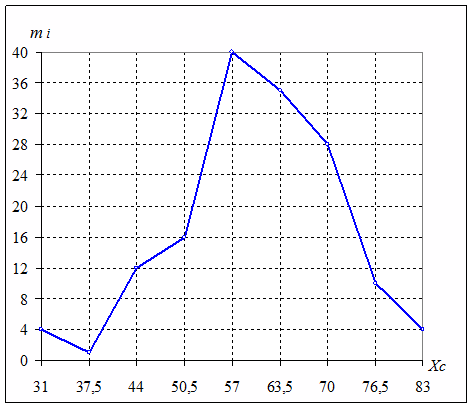
Рис.1 Полигон частот
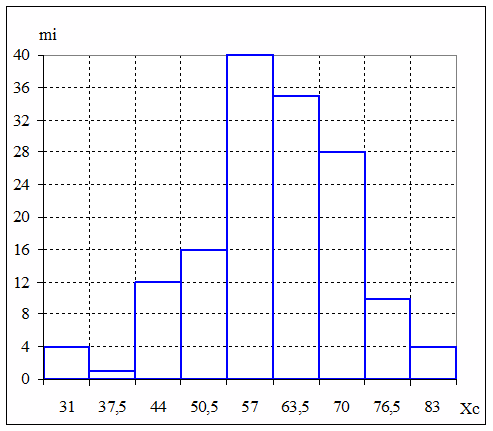
Рис.2 Гистограмма частот
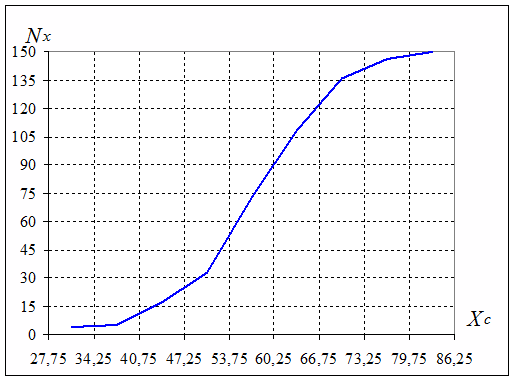
Рис.3 Огива (кумулята)
Генеральной совокупности
Рассмотрим теперь ситуацию, как будто бы нам изначально не были известны параметры распределения генеральной совокупности, но можно считать, что выборка взята по случайному закону.
В этом случае появляется возможность проверить гипотезу о том, что генеральная совокупность является нормальной. При этом снова примем α = 0,05.
Так как параметры µ и s основного распределения теперь нам неизвестны, используем совместные оценки максимума правдоподобия, исчисленные на основании группировки (таблица 3). Такими оценками являются выборочная средняя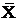 
для математического ожидания μ и исправленная выборочная дисперсия 
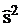для дисперсии 
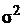. По формулам 
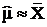и 
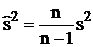, находим: 
; 
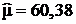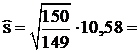10,62
В таблице 10, рассчитанной на листе «Пирсон 2» аналогично таблице 8, показано вычисление теоретических частот, а из таблицы 11 (аналог таблицы 9) по формуле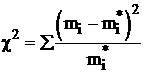 
находим χ2 = 4,59.
Таблица 10. Вычисление нормальных частот для выборки 150 изделий с параметрами: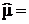 
60,38; 
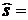10,62
| Диапазон | Интеграл вероятности | Первая разность | Частота | ||
 |  |  |  |  |  |
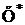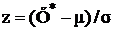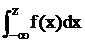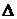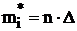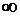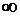| .... | -  | - | 0,00106135 | 0,15920286 | |
| 27,75 | -3,073 | 0,00106135 | |||
| 27,75 | -3,073 | 0,00106135 | 0,00587675 | 0,88151319 | |
| 34,25 | -2,460 | 0,00693811 | |||
| 37,5 | 34,25 | -2,460 | 0,00693811 | 0,0253342 | 3,80012951 |
| 40,75 | -1,848 | 0,03227230 | |||
| 40,75 | -1,848 | 0,03227230 | 0,07589259 | 11,3838885 | |
| 47,25 | -1,236 | 0,10816489 | |||
| 50,5 | 47,25 | -1,236 | 0,10816489 | 0,15805244 | 23,7078658 |
| 53,75 | -0,624 | 0,26621733 | |||
| 53,75 | -0,624 | 0,26621733 | 0,22889932 | 34,3348973 | |
| 60,25 | -0,012 | 0,49511665 | |||
| 63,5 | 60,25 | -0,012 | 0,49511665 | 0,23056748 | 34,5851215 |
| 66,75 | 0,600 | 0,72568412 | |||
| 66,75 | 0,600 | 0,72568412 | 0,16153373 | 24,2300597 | |
| 73,25 | 1,212 | 0,88721786 | |||
| 76,5 | 73,25 | 1,212 | 0,88721786 | 0,07869984 | 11,8049766 |
| 79,75 | 1,824 | 0,96591770 | |||
| 79,75 | 1,824 | 0,96591770 | 0,02665634 | 3,99845091 | |
| 86,25 | 2,436 | 0,99257404 | |||
| .... | 86,25 | 2,436 | 0,99257404 | 0,00742596 | 1,11389412 |
| | | ||||
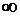| Сумма |
Таблица 11. Вычисление χ2 для выборки 150 изделий с параметрами: 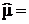60,38; 
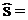10,62
| Границы теоретических интервалов | m | m* | m - m* | (m - m*)2 |  |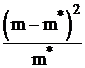
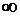| - ÷ 40,75 | 4,84084 | 0,15915443 | 0,025330 | 0,00523258 | |
| 40,75 ÷ 47,25 | 11,3838 | 0,61611151 | 0,379593 | 0,03334479 | |
| 47,25 ÷ 53,75 | 23,7078 | -7,70786578 | 59,41119 | 2,50596977 | |
| 53,75 ÷ 60,25 | 34,3348 | 5,66510268 | 32,09338 | 0,93471631 | |
| 60,25 ÷ 66,75 | 34,5851 | 0,41487848 | 0,172124 | 0,00497683 | |
| 66,75 ÷ 73,25 | 24,2300 | 3,76994035 | 14,21245 | 0,58656274 | |
| 73,25 ÷ 79,75 | 11,8049 | -1,80497664 | 3,257940 | 0,27598027 | |
| 79,75 ÷ 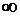| 5,11234 | -1,11234503 | 1,237311 | 0,24202425 | |
| Всего | 150,00 | -2,6645E-15 | 110,7893 | 4,58880754 |
При этой проверке критерий χ2 имеет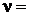 
5 степеней свободы, а 3 степени свободы потеряны, так как согласование наблюденных и теоретических частот осуществлялось из трёх условий:
; 
; 
.
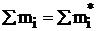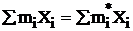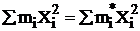Это означает, что из 8 групповых частот любые пять можно взять случайно или произвольно, но выбор 3-х остальных групповых частот нельзя осуществлять произвольно, т.к. наблюденные и теоретические распределения должны иметь одинаковые количество элементов, средние и стандартные отклонения.
Воспользовавшись функцией ХИ2ОБР(a;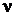 
), находим 
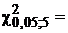11,07. Значит, область принятия определяется соотношением χ2 < 11,07.
Так как вычисленное значение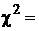 
4,59 лежит в области принятия, гипотеза Н0, что генеральная совокупность, из которой взята эта случайная выборка, является нормальной, не отвергается.
Генеральной совокупности
Продолжаем рассматривать ситуацию изначально неизвестных параметров распределения генеральной совокупности. В этом случае появляется возможность оценить эти параметры.
Мы установили в разделе 8, что гипотеза о том, что генеральная совокупность является нормальной, не противоречит выборочным данным. Теоретическая функция плотности нормального распределения включает два параметра: математическое ожидание μ и среднеквадратическое отклонение σ. Точечные оценки этих параметров вычислены ранее и равны, соответственно, генеральной средней 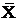=60,38 и выборочному среднеквадратическому отклонению =10,58
Т.к. теоретическая дисперсия нам неизвестна, интервальную оценку математического ожидания найдем по формуле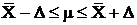 
, где предельная ошибка выборки равна 
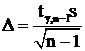. Здесь 
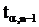- критическое значение t-распределения Стьюдента для доверительной вероятности 
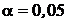и числе степеней свободы 
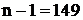. Величину 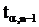находим с помощью функции «=СТЬЮДРАСПОБР(0,05;149)»: 
=1,98.
Вычисляем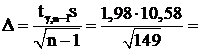 
1,72 и тогда искомый доверительный интервал для математического ожидания есть ( 
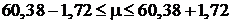) или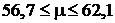 
. Нетрудно видеть, что в действительности известная нам величина 
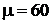находится практически в центре этого интервала.
Если имеется выборка из нормально распределенной генеральной совокупности, то случайная величина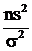 
имеет распределение 
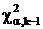с k=n-1 степенями свободы. Отсюда доверительный интервал для генеральной дисперсии: 
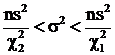. Задавая доверительную вероятность 
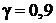, значения 
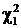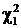и находим для k=n-1=149 как 
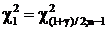и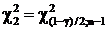 
с помощью функции «=ХИ2ОБР((1±g)/2;n-1)»:
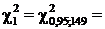121,79 и 
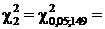178,49.
Следовательно,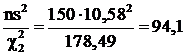 
, 
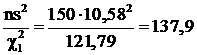, а генеральная дисперсия находится в интервале ( 
).
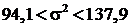При этом выборочное среднеквадратическое отклонение с надежностью 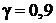находится в интервале (9,7÷11,7), что и следовало ожидать (при известном значении 
).
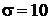Заключение
Визуальный анализ не показывает существенного расхождения между нормальной кривой и гистограммой.
χ2-критерий указывает на хорошее согласие генеральной и выборочной совокупностей.
В целом нет оснований отбрасывать гипотезу о нормальном распределении в пользу какой-то иной теоретической модели.
Параметры выборочного распределения хорошо согласуются с гипотетическими параметрами генеральной совокупности.
Все это означает, что выборка подтверждает стабильность и правильность хода изучаемого процесса.
Введение
Допустим, что изучается качество или свойство некоторого изделия (продукта) или явления в определенном технологическом (экономическом, социальном) процессе. Не умаляя общности, примем, что всего существует 1000 изделий, которые составляют «генеральную совокупность». «Не умаляя общности» означает, что с равным (для методического подхода) успехом можно принять и 10 тыс. и 10 млн. изделий.
Будем считать, что интересующее нас качество изделия определяется величиной одного из параметров (характеристик), который обозначим как признак Х.
Допустим, также, что из предшествующего опыта известно, что изучаемый параметр имеет близкое к нормальному распределение со средним значением, равным μ=60, и стандартным отклонением σ=10. Плотность распределения вероятности такого распределения задаётся формулой
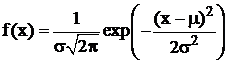
Создание генеральной совокупности
Копируем в индивидуальную рабочую папку книгу MS Excel «Шаблон» и присваиваем ей название (по фамилии студента).
Введем термин «симуляция» как понятие «моделирования», например, численного (этот термин многозначен в русском языке из-за трудности перевода англ. simulation - «моделирование»).
В качестве генеральной совокупности будем использовать несистематизированные данные, полученные в результате компьютерной симуляции 1000 наблюдений параметра.
Для компьютерной симуляции нормально распределенной случайной величины (НРСВ) используем надстройку MS Excel «Сервис \ Анализ данных \ Генерация случайных чисел»:
Вводим необходимые сведения по схеме на следующем рисунке и выходной интервал курсором указываем в ячейке А2 листа НРСВ.
В результате наблюдаем в столбце А тысячу двузначных случайных чисел. Последовательно, по 50 чисел, формируем здесь же «Таблицу НРСВ» и копируем ее в файл отчета. Файл отчета можно создать на основе данной инструкции, если скопировать ее и присвоить собственное наименование в MS Word.
Таблица НРСВ. Нормальная генеральная совокупность: N=1000, μ=60, σ=10