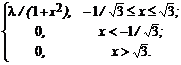Г. Схема выбора, приводящая к размещениям с повторениями
Если выбор m элементов из множества E = {e1, e2, ..., en}, производится с возвращением и с упорядочиванием их в последовательную цепочку, то различными исходами будут всевозможные m-элементные наборы (вообще говоря, с повторениями), отличающиеся либо составом элементов, либо порядком их следования. Например, при m = 4 наборы {e1, e1, e2, e1}, {e2, e1, e1, e1} и {e1, e1, e3, e1} являются различными исходами данного опыта. Получаемые в результате различные комбинации называются размещениями, с повторениями, а их общее число определяется формулой
N(W)= nm.
Пример 4. Опыт состоит в четырехкратном выборе с возвращением одной из букв алфавита E = {а, б, к, о, м} и выкладывании слова в порядке поступления букв. Какова вероятность того, что в результате будет выложено слово «мама»?
Решение. Число элементов множества, равновероятных исходов равно числу размещений с повторениями из 5 элементов по 4 т.е. N(W)= 54. Слову «мама» соответствует лишь один возможный исход. Поэтому Р(A) = N(A)/N(W) = 1/54 » 0,0016.
Д. Схема упорядоченных разбиений
Пусть множество E состоит из m различных элементов. Рассмотрим опыт, состоящий в разбиении множества E случайным образом на s подмножеств E1, E2, ..., Es таким образом, что:
1. Множество Еi содержит ровно ni элементов, где i = 1, 2, ..., s.
2. Множества Еi упорядочены по количеству элементов ni.
3. Множества Еi, содержащие одинаковое количество элементов, упорядочиваются произвольным образом. Например, при n = 7, n1 = 2, n2 = 2, n3 = 3 разбиения {E1 = {e1, е2}, Е2 = {e3, е4}, Е3 = {e5, е6, e7}} и {E1 ={e3, е4}, Е2 ={e1, е2}, Е3 = {e5, е6, e7}} являются различными исходами данного опыта.
Число всех элементарных исходов в данном опыте определяется формулой
N(W) = n!/(n1! × n2! × ... × ns!).
Пример 5. Десять приезжих мужчин, среди которых Петров и Иванов, размещаются в гостинице в два трехместных и один четырехместный номер. Сколько существует способов их размещения? Какова вероятность того, что Петров и Иванов попадут в четырехместный номер?
Решение. Разбиения в данном опыте характеризуются следующими параметрами: s = 3, n = 10, n1 = 3, n2 = 3, n3 = 4. Тогда N(W) = 10!/(3!×3!×4!) = 4200.
Пусть событие А - Петров и Иванов попадут в одни четырехместный номер. Благоприятствующие событию А исходы соответствуют разбиениям со следующими параметрами: s = 3, n = 8, n1 = 3, n2 = 3, n3 = 2. Тогда N(A) = 8!/(3!×3!×2!) = 560. Искомая вероятность Р(A) = N(A)/N(W) = 560/4200 = 2/15.
Случайные величины
Случайной величиной (СВ) Х называется действительная функция X = X(w), определенная на множестве элементарных исходов W, такая, что для любого действительного x множество тех w Î W, для которых X(w) < x, принадлежит полю событий W(W). СВ принято обозначать большими буквами латинского алфавита, а их возможные значения - соответствующими малыми буквами.
Различают СВ дискретного типа (сокращенно СВДТ) и СВ непрерывного типа (сокращенно СВНТ). СВ называется СВДТ, если множество ее возможных значений конечно или счетно. Например, число бросаний монеты до появления герба или число выпавших очков при бросании игрального кубика. СВ называется СВНТ, если множество ее возможных значений заполняют интервал числовой оси. Например, время до отказа прибора (время “жизни” прибора) или погрешность измерения.
Для полного задания СВ необходимо указать множество ее возможных значений и определить некоторое соответствие между отдельными ее значениями xi(или некоторыми подмножествами) и вероятностями pi, с которыми эти значения (или подмножества) принимаются. Любое такое соответствие называется законом распределения СВ. Например, для СВДТ достаточно указать зависимостьpi = P{X = xi} или таблицу следующего вида:
| Возможные значения СВ Х | x1 | x2 | ... | xn |
| P{X = xi} = pi > 0; (p1 + p2 + ... + pn = 1) | p1 | p2 | ... | pn |
Для СВНТ такие способы не годятся, поэтому ставят в соответствие вероятности не отдельные значения СВ, а множество значений (X < x), где x - произвольное число. Этот способ годится для СВДТ и для СВНТ.
Функцией распределения (ФР) (или интегральным законом распределения) СВ X называется числовая функция F(x) = P{X < x}, определенная для любых x Î R. Свойства ФР:
1. 0 £ F(x) £ 1;
2. F(x1) £ F(x2), если x1 < x2, т.е. F(x) - неубывающая функция;
3. 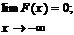
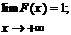
4. P{a £ X < b} = F(a) - F(b).
Плотностью распределения (ПР) (или дифференциальным законом распределения) СВ X называется числовая функция f(x), равная производной от ФР, если такая производная существует: f(x) = F¢(x). Связь между ПР и ФР можно представить в интегральной форме:
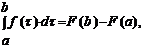 что позволяет определить ФР:
что позволяет определить ФР: 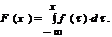
Свойства ПР:
1. f(x) ³ 0, т.к. ФР - неубывающая функция;
2. 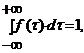 - условие нормировки.
- условие нормировки.
Задача №1. Могут ли функции j(x) и y(x) являться ФР или ПР некоторой СВ X, если “да”, то при каком значении l?
а) j(x) = 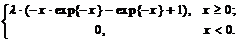 б) y(x) =
б) y(x) =