Метод Фурье решения краевых задач для уравнения Лапласа
Решение краевых задач для уравнения Лапласа в случае некоторых простейших областей (круг, сектор, кольцо, прямоугольник, шар, цилиндр) может быть найдено также методом Фурье. Получающиеся при этом задачи Штурма- Лиувилля на собственные значения приводят к различным классам специальных функций. В этом параграфе мы рассмотрим задачу Дирихле для кругового сектора и круга, при решении которых, как и в предыдущих параграфах, используются только тригонометрические функции.
При решении задач в круговом секторе или в круге удобно перейти к полярным координатам
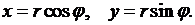
Выражая производные 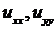 через производные по переменным
через производные по переменным 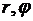 с
с
помощью формул (3.4), уравнение Лапласа 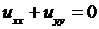 в полярных коор-
в полярных коор-
динатах можно записать в виде
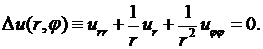 (8.1)
(8.1)
8.1. Задача Дирихле для уравнения Лапласа в круговом секторе.Найти функцию 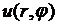 , непрерывную в замкнутом круговом секторе
, непрерывную в замкнутом круговом секторе 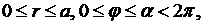 удовлетворяющую внутри кругового сектора уравнению Лапласа (8.1) и граничным условиям:
удовлетворяющую внутри кругового сектора уравнению Лапласа (8.1) и граничным условиям:
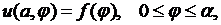 (8.2)
(8.2)
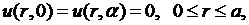 (8.3)
(8.3)
где 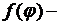 заданная функция, удовлетворяющая условию
заданная функция, удовлетворяющая условию 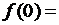
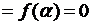 .
.
Согласно методу Фурье решение уравнения (8.1) при условиях (8.3) будем искать в виде
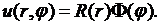 (8.4)
(8.4)
Подставляя (8.4) в уравнение (8.1), получаем
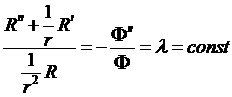 ,
,
откуда для определения неизвестных функций 
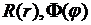 будем иметь уравнения:
будем иметь уравнения:
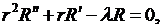 (8.5)
(8.5)
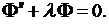 (8.6)
(8.6)
Из граничных условий (8.3) следует, что
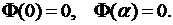 (8.7)
(8.7)
Итак, для определения функции 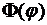 имеем задачу Штурма- Лиувилля (8.6), (8.7). Эта задача изучена нами в
имеем задачу Штурма- Лиувилля (8.6), (8.7). Эта задача изучена нами в  §§6,7. Ее решение имеет вид:
§§6,7. Ее решение имеет вид:
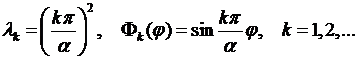 (8.8)
(8.8)
Подставляя значения 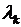 из (8.8) в уравнение (8.5), получаем
из (8.8) в уравнение (8.5), получаем
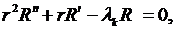 (8.9)
(8.9)
которое представляет собой однородное дифференциальное уравнение Эйлера второго порядка. Его решения можно искать в виде
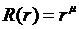 , (8.10)
, (8.10)
где 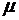 - некоторая постоянная.
- некоторая постоянная.
Подставляя (8.10) в уравнение (8.9) и сокращая на 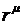 , для определения постоянной
, для определения постоянной 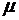 приходим к уравнению
приходим к уравнению
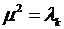 ,
,
корнями которого являются 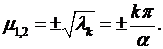 Следовательно, общее решение уравнения Эйлера (8.9) имеет вид
Следовательно, общее решение уравнения Эйлера (8.9) имеет вид
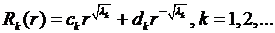 (8.11)
(8.11)
где 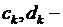 произвольные постоянные.
произвольные постоянные.
Так как решение 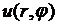 должно быть непрерывным в замкнутом круговом секторе, то
должно быть непрерывным в замкнутом круговом секторе, то 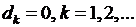 Тогда из (8.11) получим
Тогда из (8.11) получим
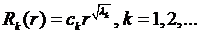 (8.12)
(8.12)
Теперь, если (8.8), (8.12) подставить в (8.4), то получим частные решения уравнения (8.1), удовлетворяющие граничным условиям (8.3), следующего вида
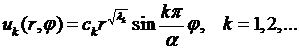
Чтобы удовлетворить условию (8.2), составим ряд из этих частных решений:
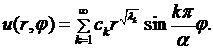 (8.13)
(8.13)
Подставляя (8.13) в условие (8.2), будем иметь:
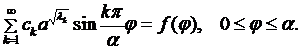 (8.14)
(8.14)
(8.14) есть разложение функции 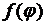 в ряд Фурье по синусам. Поступая как и в §§6,7, приходим к тому, что соотношение (8.14) будет удовлетворено, если коэффициенты разложения (8.14) определены по формулам
в ряд Фурье по синусам. Поступая как и в §§6,7, приходим к тому, что соотношение (8.14) будет удовлетворено, если коэффициенты разложения (8.14) определены по формулам
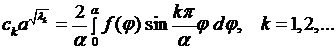
откуда
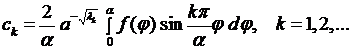 (8.15)
(8.15)
Подставляя (8.15) в (8.13), получаем решение задачи Дирихле (8.1)- (8.3).
8.2. Задача Дирихле для уравнения Лапласа в круге.Найти функцию 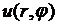 , непрерывную в замкнутом круге
, непрерывную в замкнутом круге 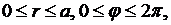 удовлетворяющую внутри круга уравнению Лапласа (8.1) и граничному условию
удовлетворяющую внутри круга уравнению Лапласа (8.1) и граничному условию
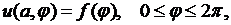 (8.16)
(8.16)
где 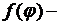 заданная непрерывная функция.
заданная непрерывная функция.
Прежде всего, заметим, что в случае круга искомая функция 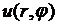 должна быть периодической с периодом
должна быть периодической с периодом 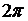 :
:
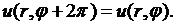 (8.17)
(8.17)
Поэтому функция 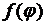 дополнительно должна удовлетворять условию
дополнительно должна удовлетворять условию
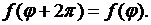
Ищем решение уравнения Лапласа (8.1), удовлетворяющее условию (8.17), снова в виде (8.4). Для определения функций 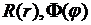 , как и в предыдущем пункте 8.1, получаем уравнения (8.5), (8.6). Условие (8.17) дает
, как и в предыдущем пункте 8.1, получаем уравнения (8.5), (8.6). Условие (8.17) дает
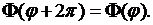 (8.18)
(8.18)
Итак, для функции 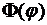 имеем задачу Штурма- Лиувилля (8.6), (8.18). Решаем ее. Рассмотрим три случая.
имеем задачу Штурма- Лиувилля (8.6), (8.18). Решаем ее. Рассмотрим три случая.
1) 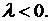 Общее решение уравнения (8.6) имеет вид:
Общее решение уравнения (8.6) имеет вид:
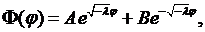
где 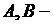 произвольные постоянные. Ясно, что ни при каких постоянных
произвольные постоянные. Ясно, что ни при каких постоянных 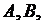 не равных одновременно нулю,
не равных одновременно нулю, 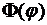 не является периодической, т.е. не выполняется условие (8.18), а значит, задача Штурма- Лиувилля в этом случае не имеет решения.
не является периодической, т.е. не выполняется условие (8.18), а значит, задача Штурма- Лиувилля в этом случае не имеет решения.
2) 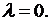 Общее решение уравнения (8.6)
Общее решение уравнения (8.6)
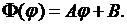
Из условия (8.18) следует, что 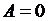 , следовательно, задача Штурма- Лиувилля имеет решение вида
, следовательно, задача Штурма- Лиувилля имеет решение вида
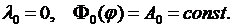
3) 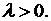 Общее решение уравнения (8.6) есть
Общее решение уравнения (8.6) есть
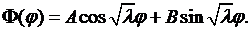
Это решение будет удовлетворять условию периодичности (8.18) лишь при 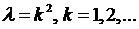
Таким образом, решения задачи Штурма- Лиувилля (8.6), (8.18) имеют вид:
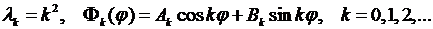 (8.19)
(8.19)
(отрицательные значения 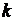 не дают новых решений), где
не дают новых решений), где 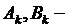 произвольные постоянные.
произвольные постоянные.
Теперь значения 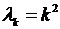 подставим в уравнение (8.5) и, рассуждая как в пункте 8.1, находим его решения в виде
подставим в уравнение (8.5) и, рассуждая как в пункте 8.1, находим его решения в виде
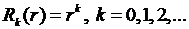 (8.20)
(8.20)
Внося выражения 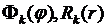 из (8.19), (8.20) в (8.4), получаем частные решения уравнения Лапласа (8.1), удовлетворяющие условию периодичности (8.17), в виде
из (8.19), (8.20) в (8.4), получаем частные решения уравнения Лапласа (8.1), удовлетворяющие условию периодичности (8.17), в виде
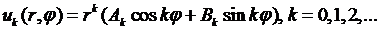 (8.21)
(8.21)
Чтобы удовлетворить граничному условию (8.16), из частных решений (8.21) образуем ряд
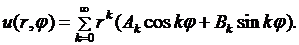 (8.22)
(8.22)
Подставляя (8.22) в граничное условие (8.16), получаем
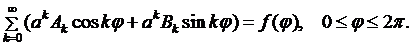
 (8.23)
(8.23)
Ряд слева в (8.23) есть полный тригонометрический ряд Фурье для отрезка 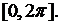 Поэтому мы удовлетворим условию (8.23), если положим
Поэтому мы удовлетворим условию (8.23), если положим 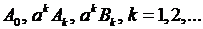 равными коэффициентам Фурье функции
равными коэффициентам Фурье функции 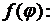
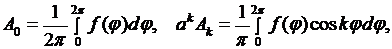
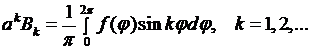 (8.24)
(8.24)
Подставляя значения коэффициентов 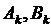 из (8.24) в (8.22), получаем решение задачи Дирихле для уравнения Лапласа в круге.
из (8.24) в (8.22), получаем решение задачи Дирихле для уравнения Лапласа в круге.
Отметим, что построенные решения задачи Дирихле в круговом секторе (8.13) и в круге (8.22) являются формальными. Для их обоснования необходимо провести те же рассуждения, что и в случае уравнения колебаний струны (§6).
В заключение отметим, что решение задачи Дирихле в круге (8.22) можно представить в виде
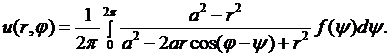
Эта формула называется формулой Пуассона, а интеграл справа – интегралом Пуассона.
Пример 8.1.Решить методом Фурье краевую задачу для уравнения Лапласа в круговом секторе 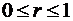 ,
, 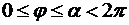 :
:
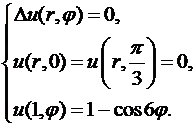
Решение.Решение этой задачи дается формулой (8.13), в которой коэффициенты определены соотношениями (8.15). В нашем случае
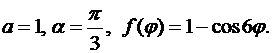
Подставляя эти значения в (8.15), для определения коэффициентов 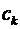 получаем
получаем 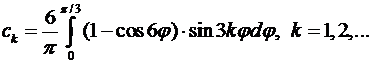 Вычислим интегралы:
Вычислим интегралы:
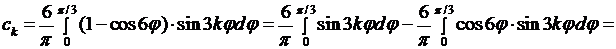
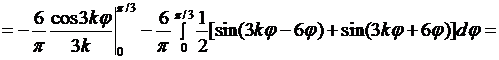
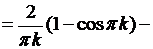
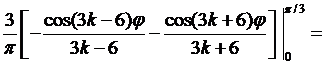
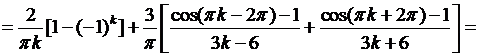
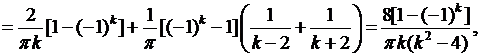 если
если 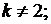
при 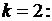
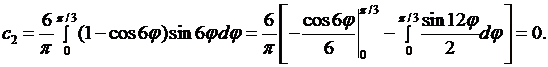
Таким образом, все коэффициенты 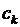 с четными номерами равны нулю.
с четными номерами равны нулю.
Теперь, подставив найденные значения коэффициентов 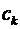 в формулу (8.13), получим решение исходной задачи в следующем виде
в формулу (8.13), получим решение исходной задачи в следующем виде
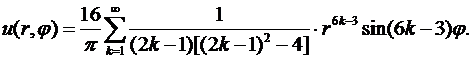
Пример 8.2.Решить методом Фурье краевую задачу для уравнения Лапласа в круге 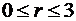 ,
, 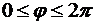 :
:
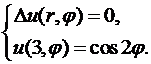
Решение.Решение этой задачи дается формулой (8.22), в которой коэффициенты 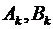 определены при помощи соотношений (8.24). Сначала коэффициенты
определены при помощи соотношений (8.24). Сначала коэффициенты 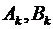 найдем с помощью (8.24). Так как в нашем случае
найдем с помощью (8.24). Так как в нашем случае 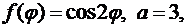 то из формул (8.24) будем иметь:
то из формул (8.24) будем иметь:
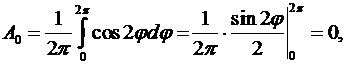
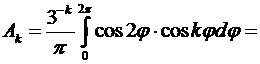
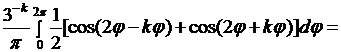
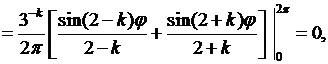 если
если 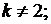
при 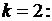
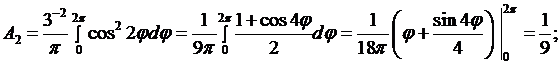
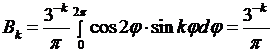
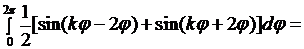
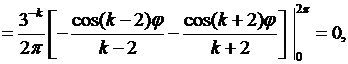 если
если 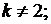
при 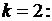
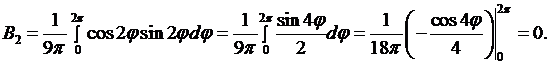
Внося найденные значения коэффициентов в формулу (8.22), получаем решение исходной задачи в виде
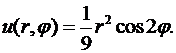
Второй способ нахождения коэффициентов 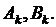 Функцию (8.22) подставим в граничное условие:
Функцию (8.22) подставим в граничное условие:
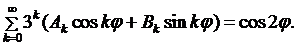
Сравнивая коэффициенты при 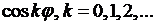 и
и 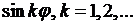 , для определения
, для определения 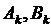 получаем
получаем
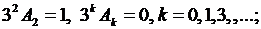
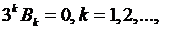
откуда 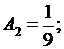 остальные
остальные 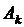 и все
и все 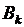 равны нулю.
равны нулю.
Задачи
Методом Фурье найти решения следующих краевых задач для уравнения Лапласа:
8.1. 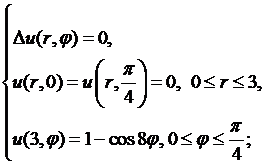 8.2.
8.2. 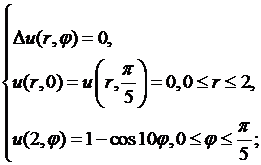
8.3. 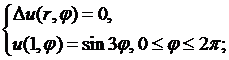 8.4.
8.4. 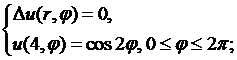
8.5. 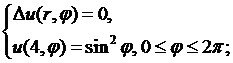 8.6.
8.6. 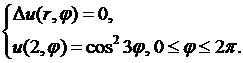

Использованная литература
1.Тихонов А.Н., Самарский А.А. Уравнения математической физики.- М.: Наука, 1972.- 736 с.
2. Крикунов Ю.М. Лекции по уравнениям математической физики и интегральным уравнениям.- Казань: Изд-во Казанск. ун-та,1970.- 210 с.
3. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике.- М.: Физматлит,2004.-688 с.
4. Вуколов Э.А., Ефимов А.В., Земсков В.Н. и др. Сборник задач по математике для втузов. Ч.4. Методы оптимизации. Уравнения в частных производных. Интегральные уравнения.- М.: Наука,1990.-304 с.
Содержание
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
§1. Основные понятия и определения . . . . . . . . . . . . . . . . . . . . . . . . 3
§2. Основные дифференциальные уравнения математической физики. Постановка задач . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.1. Малые поперечные колебания струны . . . . . . . . . . . . . . . . .. .. . 5
2.2. Распространение тепла в изотропном твердом теле . . . . . . . . 9
2.3. Установившаяся температура в однородном теле . . . . . . . . . 12
§3. Классификация и приведение к каноническому виду уравнений с частными производными второго порядка с двумя независимыми переменными . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
§4. Нахождение общих решений некоторых дифференциальных уравнений с частными производными . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
§5. Метод Даламбера решения задачи Коши для уравнения свободных колебаний струны . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
§6. Метод Фурье решения смешанных задач для уравнения колебаний струны . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.1.Случай свободных колебаний. Однородные граничные усло-
вия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.2. Случай вынужденных колебаний. Однородные граничные условия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . 31
6.3. Случай вынужденных колебаний. Неоднородные граничные условия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
§7. Метод Фурье решения начально- краевых задач для уравнения теплопроводности в тонком стержне . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
7.1. Случай однородного уравнения . . . . . . . . . . . . . . . . . . . . . . . . 39
7.2. Случай неоднородного уравнения . . . . . . . . . . . . . . . . . . . . . . 41
§8. Метод Фурье решения краевых задач для уравнения Лапласа . 46
8.1. Задача Дирихле для уравнения Лапласа в круговом секторе . 47
8.2. Задача Дирихле для уравнения Лапласа в круге . . . . . . . . . . 49
Использованная литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
