Общая схема исследования функции и построение ее графика

Исследование функции и построение её графика целесообразно проводить по следующей схеме.

1. Найти область определения функции. Установить точки разрыва и интервалы непрерывности функции.

2. Исследовать функцию на четность, нечетность, периодичность.

3. Найти точки пересечения графика функции с осями координат и промежутки знакопостоянства функции.

4. Найти точки экстремума функции, вычислить значение функции в этих точках. Установить интервалы монотонности функции.

5. Найти точки перегиба графика функции, вычислить значения функции в этих точках. Установить интервалы вогнутости и выпуклости функции.

6. Найти асимптоты графика функции. Вычислить предельные значения функции в точках, граничных для ее области существования.

7. Построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти ещё несколько точек графика функции, исходя из её уравнения.

Пример. Исследовать функцию у = 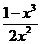и построить её график.

Решение.

1. Функция у = 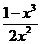определена на всей числовой оси, кроме точки x = 0.

В этой точке функция имеет бесконечный разрыв: при x → -0 и при x → +0 lim у = +∞. Во всех других точках числовой оси функция непрерывна.

2. Исследуем функцию на четность, нечетность, периодичность.

у (-х) = = ;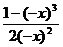

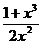у (-х) ≠ у (х) и у (-х) ≠ - у (х) – функция не является ни четной, ни нечетной.

Функция не является периодической.

3. График функции пересекает ось Ох в точке (1;0) и не пересекает оси Оу.

Если х 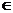(-∞; 0), у > 0; если х 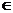(0; 1), у > 0; если х 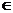(1; -∞), у < 0.

4. у' = - 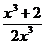; у' = 0 в точке х = - 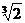, которая является критической; у' не существует в точке х = 0, но эта точка не является критической, так как она является точкой разрыва.

Исследуем критическую точку по знаку у'.

Если х 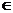(-∞; - 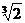), у' < 0 функция убывает; х 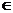(- 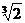; 0), у' > 0 функция возрастает. Значит х = - 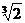является точкой минимума: у_min = .

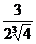На промежутке (0; -∞) у' < 0, следовательно функция убывает.

Составим таблицу

х	(-∞; - 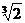)	-	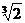(- 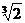; 0)		(0; -∞)
у'	-		+	не сущ	-
у		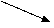		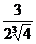не сущ

5. у'' = 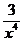; у'' ≠ 0; у'' не существует при х = 0, но это значение не может быть абсциссой точки перегиба, так как является точкой разрыва. Следовательно, график функции не имеет точек перегиба.

Во всей области определения у'' > 0, поэтому её график всюду обращен выпуклостью вниз.

6. а) Прямая х = 0 (ось ординат) является вертикальной асимптотой графика функции, так как она имеет бесконечный разрыв;

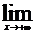
б) k = , k = = - ;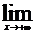

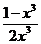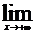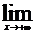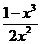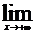
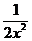b = (у - k х), b = ( + х) = = 0.

Следовательно, прямая у = - 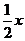является невертикальной асимптотой.

7. Используя полученные данные, строим график функции у = .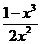

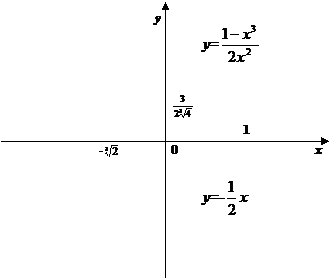
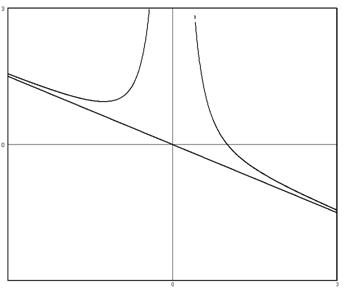
Рис. 12.

٭ ٭

٭

176. Доказать, что функция у = х⁵ + 2х³ + х возрастает, а функция у = 1 – 2х³ убывает на множестве всех действительных чисел.

177. Определить промежутки монотонности и точки экстремума функции:

а) у = (2 – х)²(2х + 1)³; с) у = ;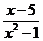

b) у = х – 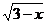; d) у = .

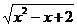178. Определить промежутки монотонности и точки экстремума функции:

а) у = х(lnх – 1); b) у = е^х – х + 1.

179. Найти наибольшее и наименьшее значения функции на указанном интервале:

а) у = х² – 6х + 8, [1; 4]; с) у = + х, [0,1; 10];

b) у = 3х⁴ + 4х³ + 1, [-2; 1]; d) у = хе^х+1, [-2; 0].

180. Найти точки перегиба и интервалы выпуклости (вогнутости) функции:

а) у = х⁴ – 2х² + 1; b) у = 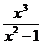; с) у = х – .

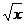181. Найти точки перегиба и интервалы выпуклости (вогнутости) функции:

а) у = lnх + ; b) у = е^2х – 4е^х + 1.

182. Найти асимптоты графика функции:

а) у = 2х³ – 9х² + 1; b) у = 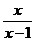; с) у = хln(1 + ).

183. Исследовать функцию и построить её график:

а) у = 3х⁴ + х² – 1; b) у = х⁵ – 2х³ + х.

184. Исследовать функцию и построить её график:

а) у = (4x² – 1)³; b) у = 2х(х + 1)².

185. Исследовать функцию и построить её график:

а) у = 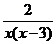; b) у = .

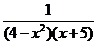186. Исследовать функцию и построить её график:

а) у = 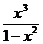; b) у = .

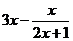187. Исследовать функцию и построить её график:

а) у = (х – 3) 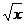; b) у = .

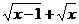188. Исследовать функцию и построить её график:

а) у = х 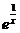; b) у = .

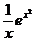189. Исследовать функцию и построить её график:

а) у = х lnx; b) у = ln (1 + x²).

c) у = х + sin х; d) у = sin х + cos x.

§3.Дифференциал функции